Problème avec la multiplication

[caro4269]

bonsoir,
notre professeur voudrait que nous démontrions que la multiplication est "commutative", c'est à dire que
a*b = b*a

j'avais pensé à un rectangle mais il considère que ce n'est pas une vraie démonstration, que ce n'est pas rigoureux
je suppose qu'il faudrait revenir à la définition première de ce qu'est une multiplication, donc une suite d'additions
c'est certainement très facile mais je ne m'en sors pas

comment prouver par exemple simplement que 6+6+6 = 3+3+3+3+3+3
j'ai toujours des bonnes notes et là je sèche, mes parents sont incapables de me répondre, tout le monde me dit que c'est évident mais personne n'est fichu de me le démontrer

[Ben314]

Bonsoir,
Il faut reconnaitre que c'est une "question à la c...".
Perso, je trouve que l'idée de le prouver avec un rectangle est excellente.
A la limite, le seul truc que je vois (mais c'est un peu con-con), c'est d'écrire que :
6+6+6=(1+1+1+1+1+1)+(1+1+1+1+1+1)+(1+1+1+1+1+1)
Si on regroupes les trois 1 qui apparaissent en premier dans chaque parenthèse, ben ça fait 3.
Si on regroupes les trois 1 qui apparaissent en deuxième dans chaque parenthèse, ben ça fait 3.
Si on regroupes les trois 1 qui apparaissent en troisième dans chaque parenthèse, ben ça fait 3.
etc...
et comme il y a six 1 dans chaque parenthèses, ben à la fin, ça fait 3+3+3+3+3+3 (6 fois)

[beagle]

Suis d'acc avec Ben314,
refuser le rectangle c'est vraiment contre productif, si j'ai a rangées de b colonnes,
rotation à 90 degrés j'ai b rangées de a colonnes.
je me souviens du temps où j'allais sur le site des instits cartables, une instit suite à une formation bananait tous les élèves avec la différence entre 7x3 et 7x3
le premier est 7 fois le 3, le deuxième est 7 multiplié par 3
et les momes ne devaient pas se gourrer,
enfin le truc débile de maniaque!

par contre ta soltion Ben314 n'est pas concon du tout,
elle permet une démonstration ensembliste
avec la patate où on regroupe a paquets de sous-ensembles contenant b unités
on a des paquets qui sont
le premier paquet b avec b11,b12,...,b1b éléments
le deuxième paquet b est b21,b22,...b2b
...
avant-dernier paquet est:
b(a-1)1,b(a-1,2)...,b(a-1,b)
le dernier paquet est
ba1,ba2, ...,bab

et comme tu le suggère judicieusement on envoie cela dans l'ensemble d'arrivée
qui lui sera composé de paquets de a
en prenant tous les b1truc pour faire le premier paquet a
tous les b2 trucs le deuxième paquet a

tous les bbtrucs pour faire le dernier paquet a
on aura b paquets a

Bijection des deux ensembles donc mème cardinal,
maintenant je sais pas si faire a paquets de b éléments c'est le axb ou le bxa moi!

Bon en fait le coté concon, tu as raison c'est qu'on a fait la mème chose que le rectangle, en plus chiant, moins intuitif,
là où c'est pas concon c'est ta façon de trouver comment dire la mème chose sans que cela se voit!!!
bravo Ben!

[Ben314]

Bon en fait le coté concon, tu as raison c'est qu'on a fait la mème chose que le rectangle, en plus chiant, moins intuitif

C'est... tout à fait ça le problème...

[caro4269]

c'est gentil à vous de vous intéresser au problème
j'ai trouvé ça sur internet,un texte de poincaré, mais sans la démonstration
il y parle de l'importance de l'apprentissage des langues même en mathématiques

"...C’est le cas du mathématicien que j’examinerai en premier et me plaçant d’abord au point de vue le plus terre à terre ; je me demanderai : est-il utile qu’il ait fait des thèmes et des versions ? La réponse nous sera fournie par une observation personnelle de M. Vacquant, inspecteur général de l’Instruction Publique pour les Mathématiques ; il inspectait un jour une classe de l’enseignement moderne, enseignement qui, je crois devoir l’ajouter, n’était pas alors ce qu’il est aujourd’hui. Il demande à un élève la démonstration d’un théorème célèbre dont tout le monde connaît l’énoncé : Le produit ne dépend pas de l’ordre des facteurs. Le jeune homme donne la démonstration qu’il a apprise dans son livre ; dans le texte il ne change qu’un petit mot, mais c’est assez pour que le raisonnement soit faux.
Je m’explique ; le signe algébrique de la multiplication peut s’énoncer de plusieurs manières : on dit quelquefois multiplié par, on peut dire aussi qui multiplie, ou bien encore que multiplie. L’auteur du livre voulait qu’on le prononçât multiplié par ou que multiplie ; l’élève avait l’habitude de l’énoncer sous la forme qui multiplie, et il n’avait eu garde, bien entendu, de changer ses habitudes pour la circonstance.
Pour tout autre théorème, cela n’aurait eu aucune espèce d’importance : a qui multiplie b, c’est la même chose que a que multiplie b, puisque l’on sait qu’on a le droit d’intervertir l’ordre des facteurs.
Pour la question posée, il en va tout autrement ; nous ne savons pas encore si l’on a le droit d’intervertir l’ordre des facteurs puisque c’est justement ce qu’il s’agit de démontrer. Nous ne savons pas encore si a qui multiplie b, c’est-à-dire un produit où le multiplicateur est a et le multiplicande b est la même chose que a que multiplie b, c’est-à-dire un produit où le multiplicateur est b et le multiplicande a ; nous n’avons pas le droit de dire l’un pour l’autre, ou bien notre démonstration devient fausse.
Malgré tous les efforts de l’inspecteur, le jeune homme ne put arriver à comprendre son erreur, et ce qui est plus surprenant, c’est qu’aucun de ses camarades ne semblait la comprendre mieux que lui. Et le professeur se désolait : « Pourtant on leur a fait faire des analyses grammaticales. » Hélas ! elles étaient bien loin, leurs analyses grammaticales.
Dans une classe de lettres, me disait M. Vacquant, rien de pareil n’aurait pu arriver ; l’erreur aurait pu être commise, mais l’élève l’aurait comprise dès qu’on la lui aurait expliquée, et réparée dès qu’il l’aurait comprise.
III
L’exemple est peut-être un peu gros et notre enseignement moderne est sans doute aujourd’hui assez bien organisé pour que le plus mal dégrossi de ses représentants soit incapable de tomber dans un semblable piège. "

c'est la question du multiplicande et du multiplicateur

[beagle]

Je ne suis pas d'accord car pour moi qui préfère a fois le b dans axb, il me reste à démontrer que c'est idem à b fois le a.
donc a fois le b, c'est b+b+b+...+b un nombre de fois a,
et je dois démontrer que c'est idem à
a+a+a+..+a b fois

si je dis axb est b qui multiplie a, alors c'est a+a+a+ b fois,
et je dois démontrer que c'est idem à bxa, a multiplie le b
qui est b+b+b+..a fois

Donc on peut prendre ce que l'on veut,
maintenant faut avoir exagéré le beaujolais nouveau pour dire je vais démontrer que
axb = a fois le b, est égal à bxa = a qui multiplie b

PS: pour démontrer que A = B, on peut partir de A et arriver à B,
mais on peut tout autant partir de B et arriver en A, donc autre raison de de ne pas comprendre la grammaire de l'inspecteur

[Dlzlogic]

Salut Beagle,
J'ai pas osé le dire avant, mais je crois me souvenir que la commutativité de la multiplication est un axiome.
Bonne soirée.

[beagle]

Salut Beagle,
J'ai pas osé le dire avant, mais je crois me souvenir que la commutativité de la multiplication est un axiome.
Bonne soirée.

ben moi le rectangle axb est de surface identique au rectangle bxa,
et s'agissant des entiers a rangées avec b colonnes rotation à 90 degrés cela donne b rangées avec a colonnes,
et si des cases ont été perdues lors de la rotation c'est qu'on a crevé le rectangle en le déplaçant et qu'il s'est dégonflé.Mais je considère cela comme de la maladresse!

[Dlzlogic]

Rassure-toi, je suis tout à fait d'accord avec l'explication du rectangle, sauf que sur le plan strictement mathématique, ça ne tient pas. En effet, il faut savoir, ou avoir décidé, ou avoir précisé que l'unité de mesure en longueur est la même que l'unité de mesure en largeur.
Pour moi, la commutativité de la multiplication est un axiome. supposons une seconde qu'il s'agisse d'une "narration de recherche" ?
Ce serait une petite satisfaction personnelle que Caro nous le dise ...

[beagle]

oui, mais si a et b sont des entiers, le cela se voit du rectangle rangées colonnes qui me suffit,
a été traduit en langage ensembliste par Ben314,
l'ensemble des éléments axb est en bijection avec l'ensembles des éléments bxa,
donc ils ont mème cardinalité.

[leon1789]

Juste pour dire que la commutativité de la multiplication des entiers n'est pas du tout un axiome. Cela se prouve facilement par récurrence (par exemple).
Mais pour une preuve niveau collège, faut peut-être faire comme Beagle et Ben314 l'indiquent. :lol3:

[leon1789]

Juste pour dire que la commutativité de la multiplication des entiers n'est pas du tout un axiome. Cela se prouve facilement par récurrence si on veut.
Pour une preuve niveau collège, faut peut-être faire comme Beagle et Ben314 l'indiquent. :lol3:
De toute manière, pour envisager une preuve, il faut revenir à une définition de la multiplication, sinon, à mon avis, c'est pédaler dans la choucroute...

[leon1789]

Juste pour dire que la commutativité de la multiplication des entiers n'est pas du tout un axiome.
De toute manière, pour envisager une preuve, il faut revenir à une définition de la multiplication, sinon, à mon avis, c'est pédaler dans la choucroute...
Pour une preuve, personnellement, je pense à de la récurrence, mais pour une preuve niveau collège, faut peut-être faire comme Beagle et Ben314 l'indiquent avec des rectangles. :lol3:

[Ben314]

Tout à fait Léon : Dans le formalisme moderne, concernant les entiers naturels, le plus fréquent est de partir des axiomes de Peano dans lesquels seul la notion de "succésseur" (i.e. la fonction a->a+1) fait parti des données de base.
Ni l'addition ni la multiplications ne sont définis et on les définis tout les deux par récurence :
1) a+b=b si a=0 et a+b=(a-1)+(b+1) si a est distinct de 0.
2) a*b=0 si a=0 et a*b=(a-1)*b+b si a est distinct de 0.
Dans ce contexte là, il faut tout démontrer (associativité, commutativité, distributivité....) et, évidement tout se démontre par récurrence (pas étonant vu les définitions...)

Aprés, concernant le texte de poincarré, perso, ça me fait surtout penser que le "formalisme à la bourbaki" où les maths ne s'écrivent qu'avec des symboles, 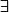et des lois 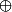, etc..., ç'est pas si con que ça : ça éviter en particulier de s'emmeler les pinceaux entre les "a multiplié par b" et "a qui multiplie b".

Exemple du point de vue d'un autre trés grand mathématitien (Hilbert) :
« Il faut toujours pouvoir dire "table", "chaise" et "bock de bière" à la place de "point", "droite" et "plan" »

[beagle]

oui, mais si c'est rond c'est point carré,
j'ai toujours pas compris pourquoi cela posait problème
a fois b égale le b fois a
ou a multiplié par b égale le b multiplié par a,
toujours pas compris comment on pouvait avoir une asymétrie dans la démonstration qui serait génante.
dans les deux cas on a un coté et faut que cela marche coté opposé, non?

que signifie cette phrase:
"nous ne savons pas encore si l’on a le droit d’intervertir l’ordre des facteurs puisque c’est justement ce qu’il s’agit de démontrer"
cela fait appel à une définition particulière de la multiplication autre que l'addition répétée????

dans les deux cas il s'agit de montrer que l'addition répétée de b un nombre a fois,
est l'addition répétée de a un nombre b fois, non?
La multiplication est définie autrement dans un cas ou dans l'autre?????

[Dlzlogic]

Salut Beagle,
Je suppose que la finesse de cette discussion réside dans le fait que certains produits, c'est à dire la multiplication de certains éléments, n'est pas commutative. De tête, un exemple, le produit vectoriel. Mais pour éviter la confusion, il est noté différemment.
N'oublions pas qu'il s'agit d'une question dans le forum "collège et primaire", et non "café mathématique".

[Ben314]

dans les deux cas il s'agit de montrer que l'addition répétée de b un nombre a fois,
est l'addition répétée de a un nombre b fois, non?

Oui, mais si tu veut faire la preuve "en français" il faut au départ que tu t'entende précisément sur le vocabulaire que tu va employer.

Si j'ai tout bien compris de ce que raconte Poincaré, des deux termes "a qui multiplie b" et "a que multiplie b", y'en a un des deux qui veut dire a+a+...+a (b fois) et l'autre qui veut dire b+b+...+b (a fois) [par contre, me demande pas lequel veut dire quoi : j'en sait rien et... je m'en fout...]

Donc si tu commence ta preuve en disant par exemple que tu va prouver que
"a qui multiplie b est égal à b que multiplie a",
ben déjà, dés le départ, t'as tout tout faux vu qu'il y a rien à démontrer...
Idem si n'importe où au milieu de ta preuve "en français" tu te goure entre les termes "qui multiplie" et "que multiplie" (d'où l'intérêt de faire le truc à l'écrit et d'utiliser le bon vieux symbole et en précisant au début ce que tu entend par ...)

Et après, pédagogiquement parlant, si j’étais instit, je présenterais axb (avec a et b entiers naturels) comme le nombres de carreaux d'un rectangle de a par b (comptés en carreaux).
Cela permet de faire des dessins expliquant pourquoi par exemple 3x(5+4)=3x5+3x4.
(Et ça règle dés le départ le problème de la commutativité)

[beagle]

Salut Beagle,
Je suppose que la finesse de cette discussion réside dans le fait que certains produits, c'est à dire la multiplication de certains éléments, n'est pas commutative. De tête, un exemple, le produit vectoriel. Mais pour éviter la confusion, il est noté différemment.
N'oublions pas qu'il s'agit d'une question dans le forum "collège et primaire", et non "café mathématique".

je comprends bien, sauf que je ne vois pas la faute, peut-ètre ne connaissant pas la définition de la multiplication dans le texte de Poincaré.
Si l'addition répétée des entiers n'était pas commutative, ben peut importe le coté par lequel tu commencerais, tu ne retomberais pas sur l'autre, c'est tout.Donc prendre un bout d'une égalité ou l'autre, rien compris ...

[beagle]

Oui, mais si tu veut faire la preuve "en français" il faut au départ que tu t'entende précisément sur le vocabulaire que tu va employer.

Si j'ai tout bien compris de ce que raconte Poincaré, des deux termes "a qui multiplie b" et "a que multiplie b", y'en a un des deux qui veut dire a+a+...+a (b fois) et l'autre qui veut dire b+b+...+b (a fois) [par contre, me demande pas lequel veut dire quoi : j'en sait rien et... je m'en fout...]

Donc si tu commence ta preuve en disant par exemple que tu va prouver que
"a qui multiplie b est égal à b que multiplie a",
ben déjà, dés le départ, t'as tout tout faux vu qu'il y a rien à démontrer...
Idem si n'importe où au milieu de ta preuve "en français" tu te goure entre les termes "qui multiplie" et "que multiplie" (d'où l'intérêt de faire le truc à l'écrit et d'utiliser le bon vieux symbole et en précisant au début ce que tu entend par ...)

c'est toujours aussi obscure, si gourer de sens alors on pose b= U et a= V,
and then on dit ensuite U= a et V=b.
Je ne comprends vraiment pas le problème de l'ordre,
puisqu'il s'agit de pouvoir inverser,
pour moi cela reste????

[Ben314]

Mais pour éviter la confusion, il est noté différemment.

Sauf que, par exemple, la multiplication des matrices ou celles des quaternion ou, de façon plus générale la loi sur un groupe non commutatif sont notés de la même façon que la multiplication sur les entiers et... ne sont pas commutatives...
La seule "convention" que je connaisse, c'est pour l'addition où, en général, on n'utilise ce symbole que dans le cas commutatif (mais il y a évidement des exceptions, par exemple avec les ordinaux où )