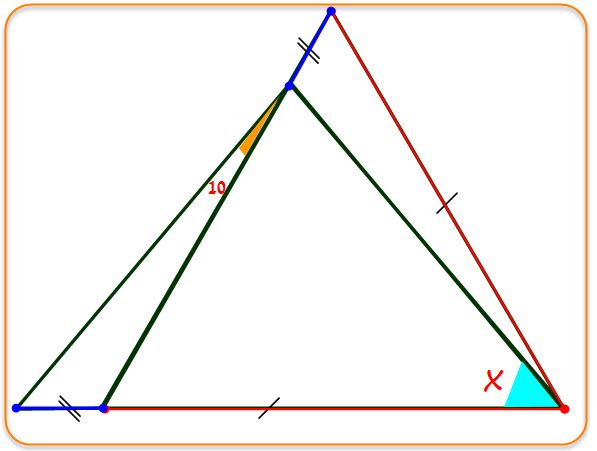
[CENTER] trouver x[/CENTER]
Ben314 a écrit:J'ai un peu regardé (je cherche plutôt le précédent qui n'a toujours pas été résolu) et j'ai bien l'impression que le dessin tel quel n'est pas suffisant à la résolution du problème, plus précisément, il me semble qu'il y a une infinité de solutions.
A mon avis, il faut en plus supposer que le triangle isocèle (dont les arrêtes sont en rouge) est en fait équilatéral.
Dans ce cas, l'angle x vaut effectivement 50° MAIS.... il faut le démontrer (géométriquement en plus...)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :