Bonjour à toutes et à tous,
Ayant beaucoup de difficultés avec le calcul d'une surface, je me suis permis de m'inscrir dans votre forum.
Voilà, j'ai fait un plan avec toutes les cotes dont je dispose. Mon problème est au niveau du calcul de surface suivant le rayon de cintrage. Je bloque complètement. :mur:
Lien pour plans : Surface
Merci d'avance pour vos réponses.
Surface avec arc
2 messages
- Page 1 sur 1
Bonjour,
Comme il y a un axe de symétrie, on peut ne s'occuper que de la moitié de la figure.
J'ai fait une figure (fausse) pour ajouter des noms aux points (cliquer sur l'image pour la voir en grand).

Données:
AH = 7.5
AB = CD = 0.697
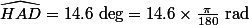
OG = OE = 15.8
On cherche l'aire en jaune + l'aire en bleu.
L'aire jaune est facile : ABCD est un parallélogramme donc son aire vaut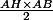
Aire en bleu = aire de OEB - aire en vert
OEB est un triangle rectangle en E (car (BC) est tangente au cercle en E), de plus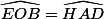 car (OB) est perpendiculaire à (AH) et (EO) est perpendiculaire à (AD).
car (OB) est perpendiculaire à (AH) et (EO) est perpendiculaire à (AD).
On a donc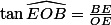 , d'où
, d'où
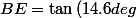} \times 15.8) .
.
On utilise ce résultat pour calculer l'aire du triangle OEB, qui vaut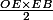 .
.
La surface verte est une portion de disque, or l'aire d'une portion de disque d'angle en radians et de rayon r est
en radians et de rayon r est 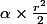 , donc l'aire en vert mesure
, donc l'aire en vert mesure 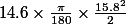 .
.
Il n'y a plus qu'à faire les calculs, additionner les aires des surfaces bleue et jaune, et multiplier par 2.
Comme il y a un axe de symétrie, on peut ne s'occuper que de la moitié de la figure.
J'ai fait une figure (fausse) pour ajouter des noms aux points (cliquer sur l'image pour la voir en grand).

Données:
AH = 7.5
AB = CD = 0.697
OG = OE = 15.8
On cherche l'aire en jaune + l'aire en bleu.
L'aire jaune est facile : ABCD est un parallélogramme donc son aire vaut
Aire en bleu = aire de OEB - aire en vert
OEB est un triangle rectangle en E (car (BC) est tangente au cercle en E), de plus
On a donc
On utilise ce résultat pour calculer l'aire du triangle OEB, qui vaut
La surface verte est une portion de disque, or l'aire d'une portion de disque d'angle
Il n'y a plus qu'à faire les calculs, additionner les aires des surfaces bleue et jaune, et multiplier par 2.
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
