Salut petite question j’ai une suite arithmétique mais avec une raison qui varie de 2 en 2 et je voudrais savoir si avec une formule je peux trouver le nombre de n’importe quel terme imaginons
U1= U0 + 10
U2= U1 + 13
U3= U2 +10
U4= U3 +13
U5= U4 +10
….
Es ce que vous auriez une formule pour trouver Un ?
Ps:(c’est faux de dire qu’elle est arithmétique mais c’est pour mieux comprendre)
Suite arithmétique
6 messages
- Page 1 sur 1
Re: Suite arithmétique
Sur la durée, pour n grand, on ajoute 23 à chaque fois qu'on avance de 2 pas. Donc on ajoute de 11.5 à chauqe pas.
Avec un correctif à apporter selon que n est pair ou impair.
Si n pair ,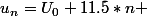 ?
?
Si n impair ,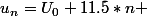 ?
?
Avec un correctif à apporter selon que n est pair ou impair.
Si n pair ,
Si n impair ,
Re: Suite arithmétique
AmadeusRochild24 a écrit:Salut petite question j’ai une suite arithmétique mais avec une raison qui varie de 2 en 2 et je voudrais savoir si avec une formule je peux trouver le nombre de n’importe quel terme imaginons
U1= U0 + 10
U2= U1 + 13
U3= U2 +10
U4= U3 +13
U5= U4 +10
….
Es ce que vous auriez une formule pour trouver Un ?
Ps:(c’est faux de dire qu’elle est arithmétique mais c’est pour mieux comprendre)
Je ne suis pas certain que la méthode de lyceen puisse fournir une expression en fonction de
Re: Suite arithmétique
@Archytas,
Non, on n'a pas :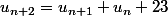 mais :
mais : 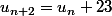
Donc, pas de Fibonacci, ni de nombre d'or.
La piste que je propose convient tout à fait.
Non, on n'a pas :
Donc, pas de Fibonacci, ni de nombre d'or.
La piste que je propose convient tout à fait.
Re: Suite arithmétique
lyceen95 a écrit:@Archytas,
Non, on n'a pas :mais :
Donc, pas de Fibonacci, ni de nombre d'or.
La piste que je propose convient tout à fait.
Oups, toutes mes excuses !
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
