Redressement de perspective
91 messages
- Page 4 sur 5 - 1, 2, 3, 4, 5
Re: Redressement de perspective
Beagle,
Un peu marre de tes attaques constantes qui sont de la pure médisance. Tes interventions n'ont aucun contenu mathématique, il s'agit juste pour toi d'exprimer ta hargne envers moi.
Bien sûr que la construction de L.A. est tout à fait correcte, c'est ce que j'ai toujours dit. Sur le rapport entre Thalès et la préservation du birapport, je te renvoie une nouvelle fois aux dessins de ce message : si on pense le premier dessin comme vue en perspective du second (avec la droite ZZ' comme droite de l'infini du plan), on voit bien que la préservation du birapport est l'outil fondamental de la géométrie projective, qui remplace le Thalès de la géométrie affine.
Je répète encore une fois que si tu avais des tuyaux précis sur l'algorithme de redressement de perspective que dlzlogic aurait mis en oeuvre dans son logiciel, je serais très intéressé. Moi, tout ce que j'ai réussi à obtenir de précis de sa part, ce sont les deux "applications de Thalès" qui donnent la construction complètement erronée de ce message.
Un peu marre de tes attaques constantes qui sont de la pure médisance. Tes interventions n'ont aucun contenu mathématique, il s'agit juste pour toi d'exprimer ta hargne envers moi.
Bien sûr que la construction de L.A. est tout à fait correcte, c'est ce que j'ai toujours dit. Sur le rapport entre Thalès et la préservation du birapport, je te renvoie une nouvelle fois aux dessins de ce message : si on pense le premier dessin comme vue en perspective du second (avec la droite ZZ' comme droite de l'infini du plan), on voit bien que la préservation du birapport est l'outil fondamental de la géométrie projective, qui remplace le Thalès de la géométrie affine.
Je répète encore une fois que si tu avais des tuyaux précis sur l'algorithme de redressement de perspective que dlzlogic aurait mis en oeuvre dans son logiciel, je serais très intéressé. Moi, tout ce que j'ai réussi à obtenir de précis de sa part, ce sont les deux "applications de Thalès" qui donnent la construction complètement erronée de ce message.
Re: Redressement de perspective
Si vous voulez jouer avec un redresseur de perspective : rendez-vous ici.
Re: Redressement de perspective
GaBuZoMeu a écrit:Enfin, si notre lecteur imaginaire veut montrer qu'il sait de quoi il parle, c'est très simple : qu'il explique clairement et précisément son algorithme de redressement : comment construire le pointà partir du point
?
L.A. a écrit:Exactement, ce n'est que du Thalès, sachant que le parallélisme dans l'espace 3D se traduit par des points de fuite en perspective...
Bilan, c'est possible de faire la transformation en n'utilisant que Thalès, L.A. l'a fait.
Re: Redressement de perspective
beagle : je l'ai répété soixante douze fois et tu refuses de l'entendre (bouché à l'émeri ou mauvaise foi ?) : Thalès dans l'espace 3D une fois projeté sur le plan de la figure par une projection centrale, ce n'est plus Thalès ; c'est la préservation du birapport. Sauf si bien sûr les parallèles restent parallèles dans la projection centrale. N'oublie pas le "sachant que" de L.A. : le point de fuite des parallèles projetées, c'est le "quatrième larron" dans les birapports de quatre points.
Et je n'ai jamais vu dlzlogic expliquer sa construction du redressement (sauf une explication qui aboutit à une construction fausse). Tout ce qu'il raconte de correct, c'est recopier mes formules (celles qui font marcher l'applet Geogebra mis en lien dans le message précédent).
PS. Désolé Idriss, je t'ai pris pour beagle, vu que tu répètes exactement ce qu'il dit.
Et je n'ai jamais vu dlzlogic expliquer sa construction du redressement (sauf une explication qui aboutit à une construction fausse). Tout ce qu'il raconte de correct, c'est recopier mes formules (celles qui font marcher l'applet Geogebra mis en lien dans le message précédent).
PS. Désolé Idriss, je t'ai pris pour beagle, vu que tu répètes exactement ce qu'il dit.
Modifié en dernier par GaBuZoMeu le 11 Mar 2020, 16:35, modifié 2 fois.
Re: Redressement de perspective
GaBuZoMeu a écrit:Thalès dans l'espace 3D une fois projeté sur le plan de la figure par une projection centrale, ce n'est plus Thalès ; c'est la préservation du birapport.
Pour le coup sur cette question on sort des maths, et on entre dans les goûts et les couleurs.
Pour toi Thalès (sachant que le parallélisme dans l'espace 3D se traduit par des points de fuite en perspective)
ce n'est pas du Thalès, c'est du bi-rapport.
Mais pour d'autres peut-être que Thalès projeté ou pas, cela reste Thalès.
Après on m'a toujours dit que les goûts et les couleurs cela ne se discutent pas.
Il ne te reste plus qu' à accepter qu'il y ait des personnes qui n'aient pas les même goûts que toi :
Est-ce si difficile, à accepter ?
Re: Redressement de perspective
Le rapport de mesures algébriques (ce dont parle Thalès) est un invariant de la géométrie affine. Quand on projette avec une projection centrale, on fait de la géométrie projective et le rapport de mesures algébriques n'est pas un invariant de la géométrie projective. C'est le birapport qui est l'invariant de la géométrie projective.
Je veux bien qu'on mélange tout, mais bon ...
Quoi qu'il en soit, même si l'on pense que le nom qu'on donne est une affaire de goût et de couleurs, la question fondamentale dans ce fil est : décrire correctement une construction de redressement de perspective (je l'ai fait et L.A. l'a fait) et expliquer correctement comment calculer les coordonnées du point redressé en fonction de celles du point de départ (je l'ai fait, et je l'ai mis en oeuvre dans l'applet Geogebra).
Je veux bien qu'on mélange tout, mais bon ...
Quoi qu'il en soit, même si l'on pense que le nom qu'on donne est une affaire de goût et de couleurs, la question fondamentale dans ce fil est : décrire correctement une construction de redressement de perspective (je l'ai fait et L.A. l'a fait) et expliquer correctement comment calculer les coordonnées du point redressé en fonction de celles du point de départ (je l'ai fait, et je l'ai mis en oeuvre dans l'applet Geogebra).
Re: Redressement de perspective
GaBuZoMeu a écrit:Désolé Idriss, je t'ai pris pour beagle, vu que tu répètes exactement ce qu'il dit.
Sans problème, en effet il m'arrive souvent d'être d'accord avec d'autres personnes que moi même.
GaBuZoMeu a écrit:expliquer correctement comment calculer les coordonnées du point redressé en fonction de celles du point de départ (je l'ai fait, et je l'ai mis en oeuvre dans l'applet Geogebra).
L.A. a écrit:OK, alors disons que je n'utilise que trois axiomes : tracer une droite passant par deux points, trouver l'intersection de deux droites, et tracer la perpendiculaire à une droite passant par un point.
En termes de coordonnées il n'y a ma foi que du degré 1...
Modifié en dernier par Idriss le 11 Mar 2020, 16:39, modifié 1 fois.
Re: Redressement de perspective
"beagle : je l'ai répété soixante douze fois et tu refuses de l'entendre (bouché à l'émeri ou mauvaise foi ?) "
euh, Idriss c'est pas beagle.
Je veux bien qu'on mélange tout Thalès les rapports bi…, mais bon!
euh, Idriss c'est pas beagle.
Je veux bien qu'on mélange tout Thalès les rapports bi…, mais bon!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: Redressement de perspective
Idriss a écrit:Bilan, c'est possible de faire la transformation en n'utilisant que Thalès, L.A. l'a fait.
Réduire la présentation de L.A. à la simple utilisation du théorème de Thalès est réducteur... c'est le moindre que l'on puisse dire. L.A. a bien parlé d'autres choses également, alors pourquoi nier le reste de sa présentation ?
Re: Redressement de perspective
Je cite :
L.A. a écrit:Exactement, ce n'est que du Thalès, sachant que le parallélisme dans l'espace 3D se traduit par des points de fuite en perspective. Ici la ligne de fuite (MI) qui traverse le prisme droit GCDHEF est parallèle (dans l'espace 3D) aux arêtes (GC) et (HE) car même point de fuite L, le triangle JIM est donc semblable au triangle DCG.
Pour terminer le tracé, on construit P l'intersection de (BM) et (GD) puis Q tel que (NH), (KF), (QM) et (AB) soient concourantes, et tel que (QP) parallèle à (GN). Alors les triangles MPQ et HGK sont semblables (dans l'espace 3D), et le point I du rectangle CDFE vu en perspective correspond au point Q sur le rectangle DKNG vu de face, modulo une éventuelle symétrie centrale appliquée à DKNG
Je précise que c'est un peu mon dada aussi, mais plus dans la version règle équerre et compas.
Re: Redressement de perspective
et après, LA. n'a rien écrit de plus , dans ces messages suivants ! ... Est-ce L.A. n'a pas nuancé ses propos ?.... alors... il ne parle pas de projection dans R^3 affine , symétrie, etc, etc. ??
Exactement, ce n'est que du Thalès, sachant que le parallélisme dans l'espace 3D se traduit par des points de fuite en perspective. Ici la ligne de fuite (MI) qui traverse le prisme droit GCDHEF est parallèle (dans l'espace 3D) aux arêtes (GC) et (HE) car même point de fuite L, le triangle JIM est donc semblable au triangle DCG.
Pour terminer le tracé, on construit P l'intersection de (BM) et (GD) puis Q tel que (NH), (KF), (QM) et (AB) soient concourantes, et tel que (QP) parallèle à (GN). Alors les triangles MPQ et HGK sont semblables (dans l'espace 3D), et le point I du rectangle CDFE vu en perspective correspond au point Q sur le rectangle DKNG vu de face, modulo une éventuelle symétrie centrale appliquée à DKNG
Re: Redressement de perspective
Désolé Beagle, je n'ai pas réalisé que c'était un nouveau venu qui reprenait tes interventions et je t'ai confondu avec Idriss.
Idriss : j'avais déjà lu, et ça ne change rien à ce que j'ai écrit plus haut (tu as oublié de mettre en gras le "sachant que").
J'ajoute qu'en termes de coordonnées plutôt que de dire "il n'y a que du degré 1", il serait plus correct de dire "il n'y a qu'une homographie".
Idriss : j'avais déjà lu, et ça ne change rien à ce que j'ai écrit plus haut (tu as oublié de mettre en gras le "sachant que").
J'ajoute qu'en termes de coordonnées plutôt que de dire "il n'y a que du degré 1", il serait plus correct de dire "il n'y a qu'une homographie".
Modifié en dernier par GaBuZoMeu le 11 Mar 2020, 17:02, modifié 1 fois.
Re: Redressement de perspective
@leon1789 : Le plus simple c'est de demander à L.A. , confirme-t-il que sa construction repose essentiellement sur l'utilisation de Thalès ?
GaBuZoMeu a écrit:J'ajoute qu'en termes de coordonnées plutôt que de dire "il n'y a que du degré 1", il serait plus correct de dire "il n'y a qu'une homographie".
Idriss a écrit:Après on m'a toujours dit que les goûts et les couleurs cela ne se discutent pas.
Il ne te reste plus qu' à accepter qu'il y ait des personnes qui n'aient pas les même goûts que toi :
Est-ce si difficile, à accepter ?
Modifié en dernier par Idriss le 11 Mar 2020, 17:05, modifié 1 fois.
Re: Redressement de perspective
Idriss a écrit:L.A. a écrit:OK, alors disons que je n'utilise que trois axiomes : tracer une droite passant par deux points, trouver l'intersection de deux droites, et tracer la perpendiculaire à une droite passant par un point.
En termes de coordonnées il n'y a ma foi que du degré 1...
Et là, pourquoi as-tu "engraissé" cette dernière phrase ? Elle pose un souci ?
Re: Redressement de perspective
Idriss a écrit:GaBuZoMeu a écrit:J'ajoute qu'en termes de coordonnées plutôt que de dire "il n'y a que du degré 1", il serait plus correct de dire "il n'y a qu'une homographie".Idriss a écrit:Après on m'a toujours dit que les goûts et les couleurs cela ne se discutent pas.
Il ne te reste plus qu' à accepter qu'il y ait des personnes qui n'aient pas les même goûts que toi :
Est-ce si difficile, à accepter ?
Oula, je sens qu'il y a une confusion entre les endomorphismes linéaires de R^3 et les homographies du plan... C'est pas une histoire de couleurs, c'est quand assez différents, bien que les deux soient liés dans l'histoire projective. Remarque, si on commence à dire que les rationnels a/b sont des entiers (a,b), pourquoi pas. Mais alors, on ne va plus se comprendre très longtemps. Déjà que le théorème de Thalès commence à ne plus être le théorème de Thalès, on n'est plus à ça... on peut mettre des couleurs partout, et dire que tout est pareil. C'est vraiment super pour comprendre.
Re: Redressement de perspective
leon1789 a écrit:Oula, je sens qu'il y a une confusion entre ...
1/ Il n'y a aucune confusion, L.A nous présente une méthode sur laquelle il dit : "...ce n'est que du Thalés..."
2/ Ensuite il explique que pour sa construction, il n' a besoin que de savoir calculer :
" une droite passant par deux points, "l'intersection de deux droites" et "la perpendiculaire à une droite passant par un point"
3/ Ce qui est vraisemblablement des calculs de degré 1 (à base d'équation de degré 1).
Cette construction porte un nom : une homographie, mais il me semble que cela n'enlève rien au point 1,2 et 3/
Ou, si ?
Re: Redressement de perspective
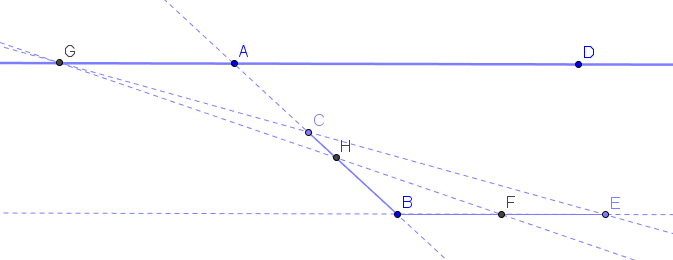
Pour mettre en évidence ma façon d'employer Thalès, je propose un autre problème plus simple.
Cette figure est une vue en perspective 2D d'un espace 3D, on se donne le segment [BC], qui est vu de biais, ainsi que son point de fuite A, qui va me permettre de gérer ce point de vue.
Le but du problème est de placer le "centre 3D" noté H du segment [BC], qui n'est pas le centre 2D classique puisque, en perspective, la moitié du segment la plus éloignée CH apparaît plus petite que la moitié la moins éloignée BH.
Ex : placer le trou du milieu H sur la vue en perspective de cette table de billard :

Ici A sera l'intersection du côté (BC) et du côté opposé.
Pour cela, je trace dans ma perspective 2D un segment [BE] et un horizon (AD) parallèle à [BE]. Dans le même temps, je place "mentalement" un point E dans l'espace 3D, et je me fixe au fur et mesure les conditions qui assurent l'unicité de cet espace et son contenu. Ici c'est simple, tous les points sont situés dans un même plan de mon espace 3D, et dans ma perspective 2D (AD) est l'horizon de ce plan, qui contient les points de fuite de toutes le droites de ce plan.
Or, comme (BE) et parallèle à (AD), l'élément [BE] n'a "pas de point de fuite", ou bien celui-ci est rejeté à l'infini. Ce qui veux dire que cet élément est vu de face, et donc que son centre 2D et son centre 3D, noté F, coïncident. Youpi, je le place.
Mon espace 3D mental contient donc un plan avec un triangle BCE et un milieu F de [BE]. J'applique dans cet espace le théorème de la droite des milieux : la parallèle à (EC) passant par F coupe [BC] en son milieu H, i.e. son "centre 3D".
Je traduis maintenant cette construction 3D mentale dans ma perspective 2D. Je trace la droite (EC) qui rencontre l'horizon (AD) en son point de fuite G, puis je trace la ligne de fuite (FG) issue de G, qui est la "parallèle 3D" à (EC) passant par F, et c'est fini.
Re: Redressement de perspective
Oui, L.A., grand classique du dessin en perspective. Dans la même veine : compléter une rangée de poteaux régulièrement espacés le long d'une voie de chemin de fer rectiligne, quand on a placé les deux premiers.
Allez, dans un esprit oecuménique, disons que c'est le théorème de Thalès dans le plan affine complémentaire de la droite (AD) du plan projectif, ou l'égalité des birapports et
et },B,E,F ]=1/2) .
.
Allez, dans un esprit oecuménique, disons que c'est le théorème de Thalès dans le plan affine complémentaire de la droite (AD) du plan projectif, ou l'égalité des birapports
Re: Redressement de perspective
Idriss a écrit:2/ Ensuite il explique que pour sa construction, il n' a besoin que de savoir calculer :
" une droite passant par deux points, "l'intersection de deux droites" et "la perpendiculaire à une droite passant par un point"
une droite passant par deux points, l'intersection de deux droites, intersection d'une droite et d'un plan (dans R^3 affine) : il n'en faut pas davantage pour commencer à s'amuser un peu en géométrie projective.
Re: Redressement de perspective
Plutôt qu'un traceur de perpendiculaire, un traceur de parallèle est pertinent dans ce contexte.
91 messages
- Page 4 sur 5 - 1, 2, 3, 4, 5
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
