Questions variées ouvertes
14 messages
- Page 1 sur 1
Questions variées ouvertes
Bonjour,
Vous pouvez posez ici toutes vos questions qui ne sont pas forcément posées au lycée ou qu'on a pas forcément le temps d'aborder à l'université. Je n'attends pas forcément de réponses mais je souhaite que ce soit un lieu où chacun expose un questionnement qu'il se pose actuellement ou qu'il s'est posé et qu'il trouve intéressant à faire partager ici.
Pour ma part je me pose la question de comment comprendre le nombre i. Si on l'utilise mal on peut aboutir a des absurdités du type 1=(-1). Je crois que dans les pays anglo-saxons on n'utilise pas comme en France la définition de i qui dit que i²=-1 mais celle ci: racine(-1)=i alors que ce n'est pas totalement vrai car racine de -1 à deux racines: i et -i. Je vous avoue que ayant défini la racine pour les nombre réels positifs et seulement positifs, l'étendre à des nombres négatifs me pose problème car j'abouti à absudités. Et alors il doit y avoir une règle établie qui tombe mais alors cela signifie que étaendre la racine aux nombres complexes est absurde.
Je vous livre mon absurdité:
1 = racine( -1 * -1) = racine(i² * i²) = i² = - 1
Qu'en pensez vous?
Vous pouvez posez ici toutes vos questions qui ne sont pas forcément posées au lycée ou qu'on a pas forcément le temps d'aborder à l'université. Je n'attends pas forcément de réponses mais je souhaite que ce soit un lieu où chacun expose un questionnement qu'il se pose actuellement ou qu'il s'est posé et qu'il trouve intéressant à faire partager ici.
Pour ma part je me pose la question de comment comprendre le nombre i. Si on l'utilise mal on peut aboutir a des absurdités du type 1=(-1). Je crois que dans les pays anglo-saxons on n'utilise pas comme en France la définition de i qui dit que i²=-1 mais celle ci: racine(-1)=i alors que ce n'est pas totalement vrai car racine de -1 à deux racines: i et -i. Je vous avoue que ayant défini la racine pour les nombre réels positifs et seulement positifs, l'étendre à des nombres négatifs me pose problème car j'abouti à absudités. Et alors il doit y avoir une règle établie qui tombe mais alors cela signifie que étaendre la racine aux nombres complexes est absurde.
Je vous livre mon absurdité:
1 = racine( -1 * -1) = racine(i² * i²) = i² = - 1
Qu'en pensez vous?
Re: Questions variées ouvertes
Bonsoir,
C'est pour cela qu'on ne parle pas de la racine carrée d'un nombre complexe (comme on en parle d'un nombre réel positif), mais des racines carrées (et nièmes) d'un nombre complexe.
1 = racine( -1 * -1) = racine(i² * i²) --> jusque là ça va
= i² = - 1 --> là ça ne va plus, il y a aussi la racine : -i²=1 car (-i²)²=i²*i²=1
Un nombre complexe n'a pas une racine carrée privilégiée comme peut l'avoir un nombre réel (on a dit que a est la racine carrée de b>=0 si a>=0 et a²=b)
C'est pour cela qu'on ne parle pas de la racine carrée d'un nombre complexe (comme on en parle d'un nombre réel positif), mais des racines carrées (et nièmes) d'un nombre complexe.
1 = racine( -1 * -1) = racine(i² * i²) --> jusque là ça va
= i² = - 1 --> là ça ne va plus, il y a aussi la racine : -i²=1 car (-i²)²=i²*i²=1
Un nombre complexe n'a pas une racine carrée privilégiée comme peut l'avoir un nombre réel (on a dit que a est la racine carrée de b>=0 si a>=0 et a²=b)
Re: Questions variées ouvertes
Bonjour,
Le nombre i est un nombre complexe dont le carré vaut -1.
C'est ainsi qu'on définit l'unité imaginaire (du moins au lycée).
Je laisse les gens du supérieur compléter ces propos ...
Le nombre i est un nombre complexe dont le carré vaut -1.
C'est ainsi qu'on définit l'unité imaginaire (du moins au lycée).
Je laisse les gens du supérieur compléter ces propos ...
Re: Questions variées ouvertes
Dire i²=-1 est je pense un raccourci qui peut prêter à des confusions du type
1 = racine (-1 * -1) = racine (i² * i²) = racine ((i²)²) = i² = -1
Dire i²=-1 peut être une approche intuitive mais je pense qu'elle masque la compréhension plus profonde de ce qu'est i. Qui dit compréhension de i dit racine complexe d'un nombre. Car qu'est ce l'invention des nombres imaginaires si ce n'est pour résoudre la racine de delta dans une équation du second degré?
Mais la racine complexe d'un nombre n'est pas une fonction comment peut-on la qualifier?
On peut juste dire que la racine complexe carrée d'un nombre à en général deux solutions.
Cela ouvre le champ sur l'ensemble C des complexes. Cela invite à penser qu'est ce qu'un ensemble?
1 = racine (-1 * -1) = racine (i² * i²) = racine ((i²)²) = i² = -1
Dire i²=-1 peut être une approche intuitive mais je pense qu'elle masque la compréhension plus profonde de ce qu'est i. Qui dit compréhension de i dit racine complexe d'un nombre. Car qu'est ce l'invention des nombres imaginaires si ce n'est pour résoudre la racine de delta dans une équation du second degré?
Mais la racine complexe d'un nombre n'est pas une fonction comment peut-on la qualifier?
On peut juste dire que la racine complexe carrée d'un nombre à en général deux solutions.
Cela ouvre le champ sur l'ensemble C des complexes. Cela invite à penser qu'est ce qu'un ensemble?
Re: Questions variées ouvertes
Salut, il y a plusieurs manière de définir 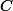 (et par conséquent
(et par conséquent  ). On peut notamment le définir comme la clôture algébrique de
). On peut notamment le définir comme la clôture algébrique de 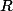 : l' "extension" de
: l' "extension" de 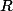 dans laquelle tout les polynômes se factorisent en produit de termes de degré 1. Mais ça demande pas mal de boulot d'arriver à ce type de construction et quelques année d'études dans le supérieur.
dans laquelle tout les polynômes se factorisent en produit de termes de degré 1. Mais ça demande pas mal de boulot d'arriver à ce type de construction et quelques année d'études dans le supérieur.
Un autre moyen pour définir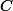 et beaucoup plus accessible (mais qui reste coriace pour le lycée) c'est de dire que
et beaucoup plus accessible (mais qui reste coriace pour le lycée) c'est de dire que 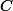 est l'ensemble des polynômes à coefficients dans
est l'ensemble des polynômes à coefficients dans 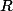 et "on dit" que
et "on dit" que 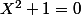 (en langage vulgaire on fait le quotient de l'anneau euclidien
(en langage vulgaire on fait le quotient de l'anneau euclidien 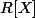 par l'idéal premier
par l'idéal premier ) et on laisse la magie de l'algèbre opérer...).
et on laisse la magie de l'algèbre opérer...).
Il doit exister encore d'autres approches de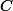 mais je doute qu'une te soit accessible avant quelques années. C'est une bonne chose de se poser la question en tout cas mais attends toi à n'avoir une réponse satisfaisante que dans quelque temps. En tout cas je suis sûr que ce charabia saura te plaire autant qu'il m'a plu si tu te poses ce genre de questions.
mais je doute qu'une te soit accessible avant quelques années. C'est une bonne chose de se poser la question en tout cas mais attends toi à n'avoir une réponse satisfaisante que dans quelque temps. En tout cas je suis sûr que ce charabia saura te plaire autant qu'il m'a plu si tu te poses ce genre de questions.
Un autre moyen pour définir
Il doit exister encore d'autres approches de
Re: Questions variées ouvertes
Je me pose la question suivante: on dit que C est un ensemble. Mais alors qu'est ce qu'un ensemble et pourquoi C en est un, qu'est ce qui dans C nous dit que c'est un ensemble?
Re: Questions variées ouvertes
Bonsoir,
Bonne question. A mon sens, C est un ensemble parce qu'on le décrète. On dit que c'est l'ensemble des nombres de la forme a+ib avec a et b réels, sur lesquels on peut effectuer les mêmes opérations que sur R et avec les mêmes règles, en rajoutant juste la règle : i²=-1. Et là, c'est magique, ce que l'on peut faire avec cet ensemble, et on se rend compte que les complexes sont un outil très puissant dans d'autres domaines qui a priori n'ont rien à y voir (géométrie, rotations, similitudes, trigonométrie, racines d'un polynôme, décomposition en éléments simples, solutions des équations différentielles, séries, ...). Mais avant de le décréter, il y a eu beaucoup de balbutiements, d'intuitions, etc... . Bref, je ne sais pas si cela répond à ta question, et j'espère que quelqu'un d'autre passera par là pour t'apporter d'autres points de vue.
Bonne question. A mon sens, C est un ensemble parce qu'on le décrète. On dit que c'est l'ensemble des nombres de la forme a+ib avec a et b réels, sur lesquels on peut effectuer les mêmes opérations que sur R et avec les mêmes règles, en rajoutant juste la règle : i²=-1. Et là, c'est magique, ce que l'on peut faire avec cet ensemble, et on se rend compte que les complexes sont un outil très puissant dans d'autres domaines qui a priori n'ont rien à y voir (géométrie, rotations, similitudes, trigonométrie, racines d'un polynôme, décomposition en éléments simples, solutions des équations différentielles, séries, ...). Mais avant de le décréter, il y a eu beaucoup de balbutiements, d'intuitions, etc... . Bref, je ne sais pas si cela répond à ta question, et j'espère que quelqu'un d'autre passera par là pour t'apporter d'autres points de vue.
Re: Questions variées ouvertes
Mais sinon, où est l'erreur dans le paradoxe suivant:
la règle est i²=-1------------------------------>par définition
ou bien la racinecpx(-1(ou i²))=i ou -i -->par définition
à partir de là:
racinecpx(-49)=racinecpx(i²*49)
=7i ou bien -7i
alors on peut aussi écrire:
1=racinecpx(-1*(-1))
racinecpx(-1*(-1))=racinecpx(i²*i²)
racinecpx(i² * i²)= i² ou -i²
donc 1=1 ou 1=-1 paradoxe, et où se cache l'erreur?
Je pense que avec les racines complexes on a pas les mêmes droits qu'avec les racines de nombres réels positifs. Mais je ne sais pas lesquelles.
la règle est i²=-1------------------------------>par définition
ou bien la racinecpx(-1(ou i²))=i ou -i -->par définition
à partir de là:
racinecpx(-49)=racinecpx(i²*49)
=7i ou bien -7i
alors on peut aussi écrire:
1=racinecpx(-1*(-1))
racinecpx(-1*(-1))=racinecpx(i²*i²)
racinecpx(i² * i²)= i² ou -i²
donc 1=1 ou 1=-1 paradoxe, et où se cache l'erreur?
Je pense que avec les racines complexes on a pas les mêmes droits qu'avec les racines de nombres réels positifs. Mais je ne sais pas lesquelles.
Re: Questions variées ouvertes
Je viens de me rendre compte que la racine complexe n'est pas la même chose que racine d'un nombre réel positif. 1 à bien deux racines complexes: 1 et -1 car leur carré donne 1 et que la racine complexe (carrée) de x est de définition: racinecpx(x) est le nombre z tel que z²=x. Par contre dans le message précédent on a aboutit à la fois sur les deux racines complexes de 1 mais on peut aussi lire 1=-1 et la je ne comprends pas ce que cela signifie à part qu'il s'agit d'un paradoxe. Comment peut-on lire cela? En fait il ne faut pas lire 1= -1 mais plutôt: racinecpx(1)=1 ou -1. Du coup 1 n'est pas égal à racinecpx(-1 * -1) comme je l'ai écrit au message précédent il faut bien faire attention à cela les racines complexes dédoublent le 1 donc l'égalité n'est plus valable.
Re: Questions variées ouvertes
Bonjour, les articles ont leur importance dans les définitions :
- La racine carrée d'un réel positif (ou nul) est la solution positive (ou nulle) de l'équation
est la solution positive (ou nulle) de l'équation 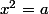 . Ainsi la racine carée de 1 est 1.
. Ainsi la racine carée de 1 est 1.
- Les racines carrées d'un complexe sont les solutions de l'équation
sont les solutions de l'équation 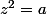 . Ainsi les racines carrées de 1 sont 1 et -1, les racines carrées de -1 sont i et -i.
. Ainsi les racines carrées de 1 sont 1 et -1, les racines carrées de -1 sont i et -i.
Bref, un nombre (complexe) a en général deux racines carrées, mais quand c'est un réel positif on peut se permettre de parler de sa racine carrée comme étant celle qui est positive, c'est celle-là qu'on note avec le symbole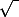 , symbole qui est à éviter quand on parle d'autre chose que des réels positifs (même s'il arrive souvent de le voir utilisé pour désigner "n'importe laquelle des racines").
, symbole qui est à éviter quand on parle d'autre chose que des réels positifs (même s'il arrive souvent de le voir utilisé pour désigner "n'importe laquelle des racines").
Cette question est en effet intéressante. Pour donner un peu plus de détails "techniques", le concept d'ensemble est axiomatique et n'a donc pas vraiment de définition : on décrète que certains objets de base sont des ensembles (typiquement l'ensemble vide et celui des entiers naturels) et on énonce des règles qui permettent de construire de nouveaux ensembles à partir d'ensemble connus (union, intersection, ensemble des parties, schéma compréhension, etc). De ce point de vue, le fait de définir les nombres complexes comme étant tous ceux qu'on peut écrire sous la forme a+ib avec a et b réels a pour conséquence que "hérite" automatiquement du statut d'ensemble de
"hérite" automatiquement du statut d'ensemble de  (qui lui-même provient d'une construction ou d'une axiomatique antérieures).
(qui lui-même provient d'une construction ou d'une axiomatique antérieures).
- La racine carrée d'un réel positif (ou nul)
- Les racines carrées d'un complexe
Bref, un nombre (complexe) a en général deux racines carrées, mais quand c'est un réel positif on peut se permettre de parler de sa racine carrée comme étant celle qui est positive, c'est celle-là qu'on note avec le symbole
Pseuda a écrit:Bonne question. A mon sens, C est un ensemble parce qu'on le décrète. On dit que c'est l'ensemble des nombres de la forme a+ib avec a et b réels, sur lesquels on peut effectuer les mêmes opérations que sur R et avec les mêmes règles, en rajoutant juste la règle : i²=-1.
Cette question est en effet intéressante. Pour donner un peu plus de détails "techniques", le concept d'ensemble est axiomatique et n'a donc pas vraiment de définition : on décrète que certains objets de base sont des ensembles (typiquement l'ensemble vide et celui des entiers naturels) et on énonce des règles qui permettent de construire de nouveaux ensembles à partir d'ensemble connus (union, intersection, ensemble des parties, schéma compréhension, etc). De ce point de vue, le fait de définir les nombres complexes comme étant tous ceux qu'on peut écrire sous la forme a+ib avec a et b réels a pour conséquence que
Re: Questions variées ouvertes
salut
il est toujours difficile effectivement de définir rigoureusement la notion d'ensemble simplement :
c'est une collection de ... (objets)
c'est une liste de ... (objets)
mais un objet est-il un ensemble ? un ensemble peut-il être un objet ?
N est l'ensemble des nombres ... mais les nombres sont aussi des ensembles puisque ce sont les classes d'équivalence pour les ensembles ... qui ont même nombre d'objets !!!
ainsi 2 est la classe d'équivalence des ensembles qui ont deux éléments : que ce soit deux fourchettes ou deux yeux, ou deux protons ou P({2}) (ensemble des parties de l'ensemble singleton {2}
pour en revenir à l'ensemble C:
tout d'abord C comme N, ou Z n'est que le nom d'un objet
ensuite une fois défini :
le produit cartésien de deux ensembles E et F noté E x F comme l'ensemble des couples (e, f) avec e dans E et f dans F (définition précise et rigoureuse)
et
la notion de structure sur un ensemble : loi interne qui en fait un groupe, anneau corps ...
alors C n'est rien d'autre que le produit cartésien de R par lui-même muni des deux opérations suivantes :
(a, b) + (c, d) = (a + c, b + d)
(a, b) * (c, d) = (ac - bd, ad + bc)
qui en font un corps
et à nouveau i n'est rien d'autre que le couple (0, 1) (donc i n'est rien d'autre que le nom du couple (0, 1)
et au final on note a + ib le couple (a, b) et R n'est rien d'autre que le sous-ensemble de C des couples (a, 0)
et on vérifie qu'avec ces notations tout roule ...
il est toujours difficile effectivement de définir rigoureusement la notion d'ensemble simplement :
c'est une collection de ... (objets)
c'est une liste de ... (objets)
mais un objet est-il un ensemble ? un ensemble peut-il être un objet ?
N est l'ensemble des nombres ... mais les nombres sont aussi des ensembles puisque ce sont les classes d'équivalence pour les ensembles ... qui ont même nombre d'objets !!!
ainsi 2 est la classe d'équivalence des ensembles qui ont deux éléments : que ce soit deux fourchettes ou deux yeux, ou deux protons ou P({2}) (ensemble des parties de l'ensemble singleton {2}

pour en revenir à l'ensemble C:
tout d'abord C comme N, ou Z n'est que le nom d'un objet
ensuite une fois défini :
le produit cartésien de deux ensembles E et F noté E x F comme l'ensemble des couples (e, f) avec e dans E et f dans F (définition précise et rigoureuse)
et
la notion de structure sur un ensemble : loi interne qui en fait un groupe, anneau corps ...
alors C n'est rien d'autre que le produit cartésien de R par lui-même muni des deux opérations suivantes :
(a, b) + (c, d) = (a + c, b + d)
(a, b) * (c, d) = (ac - bd, ad + bc)
qui en font un corps
et à nouveau i n'est rien d'autre que le couple (0, 1) (donc i n'est rien d'autre que le nom du couple (0, 1)
et au final on note a + ib le couple (a, b) et R n'est rien d'autre que le sous-ensemble de C des couples (a, 0)
et on vérifie qu'avec ces notations tout roule ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Questions variées ouvertes
Bonjour,
Votre réponse est claire zygomatique , mais une classe d'équivalence je ne vois pas trop ce que c'est. L'ensemble des parties de l'ensemble singleton {2} ça m'est un peu compliqué. Merci pour l'effort de clarté quand bien même.
Votre réponse est claire zygomatique , mais une classe d'équivalence je ne vois pas trop ce que c'est. L'ensemble des parties de l'ensemble singleton {2} ça m'est un peu compliqué. Merci pour l'effort de clarté quand bien même.
Re: Questions variées ouvertes
voir sur le net : relation d'équivalence ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
