Propriétés de l'exponentielle
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 23 Oct 2016, 09:03
par anthony_unac » 23 Oct 2016, 09:03
Bonjour,
On a tous appris un jour certaines propriétés de l'exponentielle comme par exemple :
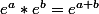
ou
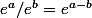
pour tout
\in R^2)
Mais existe t il des propriétés complémentaires du style :
})
ou

désigne une fonction de deux variables,

et

des réels
})
ou

désigne une fonction de deux variables,

un réel et

un rationnel.
Si vous connaissez des résultats connus ou même bricolés allant dans ce sens, je suis preneur


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Oct 2016, 11:14
par Ben314 » 23 Oct 2016, 11:14
Salut,
Ben, évidement que oui, et c'est vraiment pas la peine d'être un "balèze" des exponentielle pour le comprendre :
- Quelque soit x,y dans R, on a
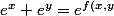})
où
=\ln(e^x\!+\!e^y))
- Quelque soit x,q dans R,
si 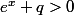 alors
alors 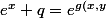})
où
=\ln(e^x\!+\!q))
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 24 Oct 2016, 08:18
par anthony_unac » 24 Oct 2016, 08:18
Salut,
Bien évidemment Ben, mais je vais être plus précis dans ma demande alors :
Existe t il une fonction

telle que
})
ou

est entier et

rationnel.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Oct 2016, 08:24
par Ben314 » 24 Oct 2016, 08:24
anthony_unac a écrit:Existe t il une fonction

telle que
})
ou

est entier et

rationnel.
Je vois pas tellement ce que ça change et la réponse est exactement la même :
Bien sûr que oui, il suffit de prendre
\!=\!\frac{1}{\pi}\ln\big(e^{\pi\sqrt{n}}\!+\!q\big))
(en supposant bien entendu que
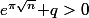
)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 24 Oct 2016, 09:03
par anthony_unac » 24 Oct 2016, 09:03
Bien sur et si on pose comme contrainte que f(n;q) ne doit pas utiliser le logarithme.
-
samoufar
- Membre Relatif
- Messages: 401
- Enregistré le: 28 Mai 2016, 17:43
- Localisation: Palaiseau
-
 par samoufar » 24 Oct 2016, 11:18
par samoufar » 24 Oct 2016, 11:18
Bonjour,
Si
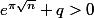
pour un certain

, on a une équivalence entre
})
et
=\frac{1}{\pi}\ln\left(e^{\pi\sqrt{n}}+q\right))
Il n'y a donc pas d'autres solutions que celle proposée par Ben.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Oct 2016, 12:02
par Ben314 » 24 Oct 2016, 12:02
anthony_unac a écrit:Bien sur et si on pose comme contrainte que f(n;q) ne doit pas utiliser le logarithme.
Ah, là, je suis "sec", mais c'est éventuellement lié au fait que je ne connait pas la définition de l'expression "la fonction f
utilise la fonction g".
Tu peut m'en donner une définition mathématique propre ?
Modifié en dernier par
Ben314 le 24 Oct 2016, 12:03, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 24 Oct 2016, 12:02
par anthony_unac » 24 Oct 2016, 12:02
Donc les cas ou
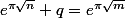
avec

et

entiers seront extrêmement rares

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
telle que
ou
est entier et
rationnel.