Probabilité suite de malchance poker

[Franck2bov]

Bonjour à toutes et a tous
Je suis joueur de poker et une question me trotte , la voici :


SI en l'espace de 29 640 mains joué je suis censé gagner +41 400 jetons ( statistique basé sur une chance "neutre" exemple : si je joue 10 000 coups avec 70% de remporter chaque coup, alors je gagne 7000 fois sur 10 000 fois, et vice versa )
Mais dès que le facteur chance est pris en compte, alors je perd -5 700 jetons au lieu d'en gagner +41 400
Alors si on estime que chaque coup est unique nous avons 1 chance sur combien d'avoir un tel écart ( je devrais gagner environ 1.41 jeton par coup, or la je gagne -0.20 jeton par coup ) pour 29 640 coups d'affilé ?

J'attends vos réponses avec impatience, Merci !

[nodgim]

Le peu que je connaisse du poker me dit que ce n'est pas lié à la chance, mais au bluff. On peut gagner une mise avec rien ou presque en main, et donc aussi perdre avec le jeu le meilleur de la table. La mémorisation des cartes des plis précédents est un atout pour favoriser la bonne décision. Le jeu en ligne n'a strictement aucun intérêt.

[Franck2bov]

Bonjour nodgim
Je suis d'accord avec toi cependant tout ça reunis ( bluff pris en compte etc ) donne ce qu'on appelle l' "EV" ; l'Expected value en anglais, l'espérance de gain. Pour mon cas mon EV sur cet exemple est de 41 400 jetons pour 29 640 mains.
Que entends tu pars "le jeu en ligne n'a strictement aucun intérêt" ?

Autre question : Si je joue 30 000 fois à pile ou face, je devrais en moyenne gagner 15 000. Or quel chance y'a t- il pour que je ne gagne que 3 000 fois et donc perd 27 000 fois avec une pièce ? Au bout de combien de pile ou face par tranche de 30 000 je peux obtenir ce résultat la ?

[LB2]

La probabilité que tu cherches pour gagner au plus 3000 fois sur 30000 lancers équilibrés de pile ou face est donnée par la fonction de répartition de la loi binomiale de paramètre 1/2 : elle est très très très faible.
Comme le nombre de lancers est grand, on peut approximer la loi binomiale par une loi normale, de moyenne 15000 et de variance 7500.

Cette probabilité est tellement faible que l'on ne la trouve pas dans les tables de la loi normale : elle est (très) inférieure à 10^{-5}

[Franck2bov]

Merci beaucoup LB2 pour ta réponse !!

Du coup c'est exactement ce que je cherches pour mes statistiques
Sachant que je suis censé faire +1.41 jetons / mains ( chance "neutre") et que aulieu de ça je fais -0.20 jeton / mains . Linéairement sur 29640 mains quel est la probabilité pour que ça arrive ?
C'est un peu comme si je jouais a pile ou face avec une pièce avec un coté plus lourd qui tomberais 1.41 fois / 2 de ce même coté, or il tombe seulement 0.80 fois / 2 de ce coté la et tout ça sur 29640 coups d'affilé, je me trompe ?

Désolé je ne suis pas si bon que ça en mathématique je ne suis pas sur de bien me faire comprendre.. En tout cas la réponse m'aiderais énormément merci beaucoup d'avance

( Suivant le résultat, peut-on dire que le jeu est finalement truqué ? )

[Franck2bov]

SVP J'ai vraiment besoin d'aide...

[Ben314]

Du coup c'est exactement ce que je cherches pour mes statistiques
Sachant que je suis censé faire +1.41 jetons / mains ( chance "neutre") et que aulieu de ça je fais -0.20 jeton / mains . Linéairement sur 29640 mains quel est la probabilité pour que ça arrive ?

Que tu ait une différence aussi grande sur un tel nombre de mains, y'a même pas besoin de se lancer dans un quelconque calcul, un minimum de bon sens suffit amplement :
- Il y a 0,000000000000000000000000001 % de chance que "tu ait pas eu de pot".
- Il y a 99,999999999999999999999999999 % de chance que tu te soit fait arnaquer.
(et encore, je suis sympa : si on te faisait le calcul exact de la proba qu'un tel événement arrive "pour de vrai", ben il y a aurait encore bien plus de zéro...)

[Franck2bov]

Bonjour Ben314 merci pour ta réponse

Je sais bien tout ça, c'est pas le bon sens qui manque… Le problème c'est que j'ai besoin du calcul exact ou sinon on continuera a parler de "variance" et non de trucage. Il me faut la preuve mathématique que le poker en ligne est bien truqué d'une manière ou d'une autre.


Si quelqu'un pourrais réaliser ce calcul ça m'aiderais énormément

[Ben314]

Pour se lancer dans un "vrai calcul", de connaître l'espérance de gain (à savoir +1.41) ce n'est pas suffisant : il faut aussi connaître au minimum l'écart type (et utiliser l'inégalité de Inégalité de Bienaymé-Tchebychev) voir même connaître la loi complète si on veut une valeur exacte (ou alors estimer que, vu le nombre colossal d'expériences, de toute façon, c'est quasi sûr qu'au final on aura un truc presque Gaussien).

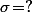Bref, si pour une partie l’espérance est jeton et l'écart type jetons, alors pour parties (indépendante les unes des autres), l'espérance de la moyenne des gains est toujours mais l'écart type lui devient et l'inégalité de Bienaymé-Tchebychev te dit que la proba d'être à une distance supérieure à (distance de à ) de la moyenne est majorée par .

[Franck2bov]

Je viens de m'apercevoir que je n'avais pas répondu, alors un grand MERCI Ben314 pour ton message et ton aide !!