Probabilité et jeux de dés
20 messages
- Page 1 sur 1
probabilité et jeux de dés
Bonjour
Voici ma question, dans un jeu où on lance simultanément 5 dés à 6 faces, j'aimerais savoir quelles sont mes chances qu'au moins 2 des 5 dés donne un résultat de 4 ou plus
en fait c'est pas vraiment la réponse dont j'ai besoin, mais plutôt de la démarche a effectuer pour trouver la bonne réponse, afin que je puisse l'appliquer à d'autres situations (plus ou moins de dés, dés avec plus ou moins de faces, chiffre à atteindre sur 1 dé plus ou moins élevé)
ma méthode pour le moment c'est de voir tous les cas possibles et d'en extraire les résultats souhaités... mais c'est long lol :)
merci à vous et bonne journée
Voici ma question, dans un jeu où on lance simultanément 5 dés à 6 faces, j'aimerais savoir quelles sont mes chances qu'au moins 2 des 5 dés donne un résultat de 4 ou plus
en fait c'est pas vraiment la réponse dont j'ai besoin, mais plutôt de la démarche a effectuer pour trouver la bonne réponse, afin que je puisse l'appliquer à d'autres situations (plus ou moins de dés, dés avec plus ou moins de faces, chiffre à atteindre sur 1 dé plus ou moins élevé)
ma méthode pour le moment c'est de voir tous les cas possibles et d'en extraire les résultats souhaités... mais c'est long lol :)
merci à vous et bonne journée
Il y a une chance sur 2 pour qu'un dé donne un 4 ou plus: 4,5,6 à comparer avec 1,2,3 il y a bien 3 faces de réussite et 3 faces d'échec.
Pour qu'aucun dé ne soit gagnant: (1/2)^5
Pour qu'un seul dé soit gagnant: 1er dé gagnant, les autres perdants: (1/2)^5 et donc pour les 5 dés: 5*(1/2)^5
Hormis ces cas, on est tjs gagnant:
1-6(1/2)^5 est la proba de faire 4 ou plus.
soit 26/32 ou 13/16.
Pour qu'aucun dé ne soit gagnant: (1/2)^5
Pour qu'un seul dé soit gagnant: 1er dé gagnant, les autres perdants: (1/2)^5 et donc pour les 5 dés: 5*(1/2)^5
Hormis ces cas, on est tjs gagnant:
1-6(1/2)^5 est la proba de faire 4 ou plus.
soit 26/32 ou 13/16.
merci de m'avoir répondu, mais j'avoue m'être perdu déjà à la 2eme ligne
donc pour qu'aucun dé ne soit gagnant : (1/2)^5 je comprends
mais 1 Gagnant et les autres perdants : (1/2)^5 aussi... ok je viens de comprendre, j'ai autant de chances de gagner que de perdre avec 1 D, si le chiffre à atteindre était 5 au lieu de 4, alors qu'aucun dé ne soit gagnant : (2/3)^5 et 1 gagnant les autres perdants : (1/3).(2/3)^4 c'est bien ça ?
par contre j'ai du mal quand même avec 1-6(1/2)^5. 1- c'est pour avoir la probabilité de réussite puisqu'on a calculé à la base les chances de faire un échec, mais le 6(1/2)^5 je ne comprend pas d'où vient le 6
et si je veux augmenter ou diminuer le nombre de succès (nombre de dés qui atteint le chiffre prévu) je dois jouer sur quelle variable ? ce 6 ?
encore merci en tous cas, même si tout n'est pas encore clair (j'essaie de faire un compromis avec mon cerveau) c'est quand même déjà plus clair qu'avant
donc pour qu'aucun dé ne soit gagnant : (1/2)^5 je comprends
mais 1 Gagnant et les autres perdants : (1/2)^5 aussi... ok je viens de comprendre, j'ai autant de chances de gagner que de perdre avec 1 D, si le chiffre à atteindre était 5 au lieu de 4, alors qu'aucun dé ne soit gagnant : (2/3)^5 et 1 gagnant les autres perdants : (1/3).(2/3)^4 c'est bien ça ?
par contre j'ai du mal quand même avec 1-6(1/2)^5. 1- c'est pour avoir la probabilité de réussite puisqu'on a calculé à la base les chances de faire un échec, mais le 6(1/2)^5 je ne comprend pas d'où vient le 6
et si je veux augmenter ou diminuer le nombre de succès (nombre de dés qui atteint le chiffre prévu) je dois jouer sur quelle variable ? ce 6 ?
encore merci en tous cas, même si tout n'est pas encore clair (j'essaie de faire un compromis avec mon cerveau) c'est quand même déjà plus clair qu'avant
Bonjour, je ne suis pas d'accord avec nodjim.
Les 6 cas possibles sont: 0 dé gagnant, 1dé gagnant, 2 dés gagnants,..., 5 dés gagnants. Il faut donc que la somme des probabilités correspondantes = 1 or 6*(1/2)^5<1. L'erreur est: P(0 dé gagnant)=(1/2)^5 ok mais P(1 dé gagnant et les autres perdants)= (1/2)*(1/2)^4*5, P(2 dés gagnants et 3 perdants)=^{2}*(\frac{1}{2})^{3}*C^{2}_{5}) etc...
etc...
D'une manière générale on aura:
P(n dés gagnants et 5-n dés perdants)=^{5}.C^{5}_{n})
Les 6 cas possibles sont: 0 dé gagnant, 1dé gagnant, 2 dés gagnants,..., 5 dés gagnants. Il faut donc que la somme des probabilités correspondantes = 1 or 6*(1/2)^5<1. L'erreur est: P(0 dé gagnant)=(1/2)^5 ok mais P(1 dé gagnant et les autres perdants)= (1/2)*(1/2)^4*5, P(2 dés gagnants et 3 perdants)=
D'une manière générale on aura:
P(n dés gagnants et 5-n dés perdants)=
Bonjour mais tu es d'accord avec nodjim.
1 seul cas pour tout foirer
et nodjim compte 5 fois la proba de base pour 1 cas seulement de réussi, qui correspond à choisir l'emplacement sur les 5 possibles du un qui marche.
Donc nodjim n'a jamais dit que 6 fois 1/2^5 faisait 1.
1 seul cas pour tout foirer
et nodjim compte 5 fois la proba de base pour 1 cas seulement de réussi, qui correspond à choisir l'emplacement sur les 5 possibles du un qui marche.
Donc nodjim n'a jamais dit que 6 fois 1/2^5 faisait 1.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
bazetof a écrit:d'accord, mais je comprend pas pourquoi
(désolé, mes cours de proba datent d'il y a 18 ans et je n'avais que 3H de math par semaine... c'est loin tout ça)
ah si... peut-être, en lisant vos réponses, en fait on lance 5 dés, mais on fait 6* car on compte 0 réussites, 1, 2, 3, 4, 5... ce qui donne 6 possibilités.... c'est ça ?
bazetof a écrit:ah si... peut-être, en lisant vos réponses, en fait on lance 5 dés, mais on fait 6* car on compte 0 réussites, 1, 2, 3, 4, 5... ce qui donne 6 possibilités.... c'est ça ?
Non, le 6x vient de la somme de 1+5.
En fait tu comprendrais bien mieux avec des probas de réussites et de pertes qui seraient de valeur différente.Dans le cas présent gagner ou perdre fait 1/2, résultat tu ne sais pas qui de gagner ou de perdre donne le 1/2^5.Par exemple 3 gains et deux pertes sont (1/2)^3 x (1/2)^2.
Si on avait gains à 2/3 et perte à 1/3, alors 3 gains et deux pertes seraient à (2/3)^3 x(1/3)^2.
Il resterait à multiplier par les possibilités différentes d'emplacement des 3 gains et 2 pertes.
Par exemple tu peut avoir:
gain-gain-perte-gain-perte
ou
perte-gain-gain-perte-gain
Donc ta proba de base en ^5 est à remultiplier par choisir les emplacements de gains et pertes,
et c'est idem de choisir 3 emplacements de gains dans 5 choix que de choisir 2 emplacements de pertes dans les 5 choix.
Donc tu dois multiplier ta praba de base par du C(3,5) par exemple.
Dans le cas de 1 gain, choisir 1 emplacement de gain sur 5 choix qui est le C(1,5) vaut 5 comme la logique ou l'intuition te le dit tout de suite.
c'est pour cela que tu avais 5x (1/2)^5
que nodjim additionnait avec 5 pertes, qui correspond à un seul choix:
perte-perte-perte-perte-perte
donc 1 x (1/2)^5
Et nodjim enlève à proba totale qui vaut 1, la proba des évènements qui ne sont pas ceux recherchés,
comme cela il obtient la proba de ce qu'il cherche.
Autrement tu devrais faire proba de 2 gains, plus proba 3 gains plus proba 4 gains ,plus proba 5 gains.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
bazetof a écrit:petit test voir si j'ai compris
je lance 7 dés à 8 faces, la cible est 6 et je veux minimum 4 succès
donc la formule deviendrait 1-(3/8)^4 x (5/8)^3 ?
8 faces la cible est 6 ou plus, donc ok pour du 3/8 et 5/8
mais tu devrais lire ceci:
http://fr.wikipedia.org/wiki/Loi_binomiale
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Pfiou je suis dépassé
A mon avis il me manque une information ou une formation
Je n'ai pas compris le truc de la loi binomiale
Alors j'ai voulu éprouver la formule
J'ai pris comme base 4 dés a 6 face, la cible est 5 et il me faut minimum 2 succès
Donc
1-(1/3)^2*(2/3)^2 = 0.95061728 (ou 1-4/81 = 77/81)
Et j'ai passé mon temps a recenser toutes les possibilités possibles (6^4 ou 1296) et voir le nombre de ces possibilités
Il y en a 528) donc 528/1296 ça fait 33/81
J'ai pensé que peut être la formule ne fonctionne que pour exactement 2 succès alors j'ai recompté mais alors on arrive a 384/1296 ou 24/81 donc c'est pas ça non plus
Bon, j'ai la bonne réponse, il me manque plus qu'à avoir la bonne formule
Mais je vais arrêter de vous embêter avec ça, le problème vient sûrement de moi
Merci malgré tout pour votre patience et bonne journée
A mon avis il me manque une information ou une formation
Je n'ai pas compris le truc de la loi binomiale
Alors j'ai voulu éprouver la formule
J'ai pris comme base 4 dés a 6 face, la cible est 5 et il me faut minimum 2 succès
Donc
1-(1/3)^2*(2/3)^2 = 0.95061728 (ou 1-4/81 = 77/81)
Et j'ai passé mon temps a recenser toutes les possibilités possibles (6^4 ou 1296) et voir le nombre de ces possibilités
Il y en a 528) donc 528/1296 ça fait 33/81
J'ai pensé que peut être la formule ne fonctionne que pour exactement 2 succès alors j'ai recompté mais alors on arrive a 384/1296 ou 24/81 donc c'est pas ça non plus
Bon, j'ai la bonne réponse, il me manque plus qu'à avoir la bonne formule
Mais je vais arrêter de vous embêter avec ça, le problème vient sûrement de moi
Merci malgré tout pour votre patience et bonne journée
Je n'ai pas eu trop le temps hier.
Si wiki loi binomiale est trop dur, cherche avec google du loi binomiale plus simple, ça doit bien exister et tu comprendras tout.
Maintenant si tu veux partir du simple au compliqué on peut rester sur ton dernier exemple en le décomposant.
4 dés 6 faces, cible 5 ou plus
mais ne parle pas pour le moment du 2 succès minimum.
le plus simple est de calculer:
zéro succès
1 seul succès
2 succès exactement
3 succès exactement
4 succès exactement
Pour zéro succès
tu auras (2/3)^4
et une seule possibilité: échec, échec, échec, échec
Pour 1 seul succés tu auras, une proba base de 1/3 (= ton succès) x (2/3)^3(= tes 3 échecs)
mais ce succès peut arriver sur le dé 1 ou le 2 ou le 3 ou le 4
si G = gain et P = perte
si on place les dés en rangée
la proba de base peut survenir pour 4 situations, 4 évènements différents
GPPP
PGPP (en fait la proba de base s'écrirait: 2/3 x 1/3 x 2/3 x 2/3, mais c'est idem)
PPGP (2/3 x2/3 x 1/3 x 2/3)
PPPG (2/3 x 2/3 x2/3 x 1/3)
donc 1 seul succès sera de proba 4 x 1/3 x (2/3)^3
Fais les suivants pour voir.
Si wiki loi binomiale est trop dur, cherche avec google du loi binomiale plus simple, ça doit bien exister et tu comprendras tout.
Maintenant si tu veux partir du simple au compliqué on peut rester sur ton dernier exemple en le décomposant.
4 dés 6 faces, cible 5 ou plus
mais ne parle pas pour le moment du 2 succès minimum.
le plus simple est de calculer:
zéro succès
1 seul succès
2 succès exactement
3 succès exactement
4 succès exactement
Pour zéro succès
tu auras (2/3)^4
et une seule possibilité: échec, échec, échec, échec
Pour 1 seul succés tu auras, une proba base de 1/3 (= ton succès) x (2/3)^3(= tes 3 échecs)
mais ce succès peut arriver sur le dé 1 ou le 2 ou le 3 ou le 4
si G = gain et P = perte
si on place les dés en rangée
la proba de base peut survenir pour 4 situations, 4 évènements différents
GPPP
PGPP (en fait la proba de base s'écrirait: 2/3 x 1/3 x 2/3 x 2/3, mais c'est idem)
PPGP (2/3 x2/3 x 1/3 x 2/3)
PPPG (2/3 x 2/3 x2/3 x 1/3)
donc 1 seul succès sera de proba 4 x 1/3 x (2/3)^3
Fais les suivants pour voir.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
oki, donc pour 2 succès j'aurai
GGPP
GPGP
GPPG
PGGP
PGPG
PPGG
ça m'a rappelé un truc ça, j'ai été chercher, c'est une combinaison c'est ça ? dans ce cas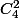 (et du coup je comprends une formule utilisée plus haut :we: )
(et du coup je comprends une formule utilisée plus haut :we: )
et la formule serait 6 x (1/3)^2 x (2/3)^2
pour 3 succès :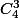 ça fait 4 possibilités
ça fait 4 possibilités
4 x (1/3)^3 x (2/3)
et pour 4 succès, ça n'en fait qu'une
1 x (1/3)^4 x (2/3)^0 donc (1/3)^4
c'est bien ça ?
GGPP
GPGP
GPPG
PGGP
PGPG
PPGG
ça m'a rappelé un truc ça, j'ai été chercher, c'est une combinaison c'est ça ? dans ce cas
et la formule serait 6 x (1/3)^2 x (2/3)^2
pour 3 succès :
4 x (1/3)^3 x (2/3)
et pour 4 succès, ça n'en fait qu'une
1 x (1/3)^4 x (2/3)^0 donc (1/3)^4
c'est bien ça ?
bazetof a écrit:oki, donc pour 2 succès j'aurai
GGPP
GPGP
GPPG
PGGP
PGPG
PPGG
ça m'a rappelé un truc ça, j'ai été chercher, c'est une combinaison c'est ça ? dans ce cas(et du coup je comprends une formule utilisée plus haut :we: )
et la formule serait 6 x (1/3)^2 x (2/3)^2
pour 3 succès :ça fait 4 possibilités
4 x (1/3)^3 x (2/3)
et pour 4 succès, ça n'en fait qu'une
1 x (1/3)^4 x (2/3)^0 donc (1/3)^4
c'est bien ça ?
Voilà c'est bien cela.
Et effectivement, tu peux maintenant relire loi binomiale et tout s'éclaire.
avoir k succés sur n tirages avec p proba de succès
ben d'abord j'ai ma proba de base
p^k x (1-p)^(n-k)
et il faut que je multiplie tout cela par les combinaisons de k éléments choisis dans n éléments,
C(k,n)
on se retrouve avec des formules comme:
C(k,n) x p^k x (1-p)^(n-k)
Après tu peux compliquer avec au moins tant ou tant de succès.
Si tu cherches au moins 2 succès sur les 4 dés,
soit tu additionnes avoir exactement 2 + avoir exactement 3 + avoir exactement 4
soit tu enlèves à la proba 1 le fait d'avoir moins de 2 succès,
1 - (proba zéro succès + proba 1 seul succès)
Voilà tu dois y ètre maintenant.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
"grand merci pour votre patience en tous cas "
Dès lors que tu proposes et qu'on avance , mème lentement, tu trouveras toujours quelqu'un sur le site.
Je voudrais juste au niveau de la rigueur qui n'est pas mon fort, plus par manque de connaissance que volonté de m'assoir dessus, si des plus jeunes scolarisés lisent cela, il faut certainement éviter sur un exo de lancer simultanée de 5 dés se lancer d'emblée dans du, ben j'applique la loi binomiale et qs.C'est un truc pour se faire battre.deux solutions:
-la première, ne pas parler de loi binomiale, mais faire les calculs comme on l'a fait (calculs qui retombent, reviennent à de la loi binomial
-la deuxième, une courte phrase pour dire que un lancer de 5 dés simultanément, c'est un lancer de 5 dés identiques (= mème probas de gain ou perte) avec indépendance entre les 5 dés.
de ce fait on peut ramener un lancer de 5 dés simultanément à un lancer de un seul dé successivement 5 fois, = mème proba p qui réalise des tirages-lancers indépendants, et que donc on peut se ramner sur loi binomiale.
bazetof je t'ai emmené sur loi binomiale pour que tu comprennes bien que la proba d'un évènement type deux gains 3 pertes, c'est la proba élémentaire p^2 x (1-p)^3,
à remultiplier par l'ensemble des évènements qui vont réaliser cela,
d'où la remultiplication par le C(2,5) que tu oubliais dans tes premières réponses.
voili, voilo, j'espère ne pas avoir dit trop de bétises.
Dès lors que tu proposes et qu'on avance , mème lentement, tu trouveras toujours quelqu'un sur le site.
Je voudrais juste au niveau de la rigueur qui n'est pas mon fort, plus par manque de connaissance que volonté de m'assoir dessus, si des plus jeunes scolarisés lisent cela, il faut certainement éviter sur un exo de lancer simultanée de 5 dés se lancer d'emblée dans du, ben j'applique la loi binomiale et qs.C'est un truc pour se faire battre.deux solutions:
-la première, ne pas parler de loi binomiale, mais faire les calculs comme on l'a fait (calculs qui retombent, reviennent à de la loi binomial
-la deuxième, une courte phrase pour dire que un lancer de 5 dés simultanément, c'est un lancer de 5 dés identiques (= mème probas de gain ou perte) avec indépendance entre les 5 dés.
de ce fait on peut ramener un lancer de 5 dés simultanément à un lancer de un seul dé successivement 5 fois, = mème proba p qui réalise des tirages-lancers indépendants, et que donc on peut se ramner sur loi binomiale.
bazetof je t'ai emmené sur loi binomiale pour que tu comprennes bien que la proba d'un évènement type deux gains 3 pertes, c'est la proba élémentaire p^2 x (1-p)^3,
à remultiplier par l'ensemble des évènements qui vont réaliser cela,
d'où la remultiplication par le C(2,5) que tu oubliais dans tes premières réponses.
voili, voilo, j'espère ne pas avoir dit trop de bétises.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
