Phi !
46 messages
- Page 1 sur 3 - 1, 2, 3
Phi !
Bonjour,
J'ai récemment découvert le nombre phi ou le nombre d'or, la solution de l'équation x² -x -1 = 0. Et je me pose pas mal de questions :
-pourquoi ce nombre est-il connu, c'est vrai par exemple avec pi on peut calculer airs et volumes qu'est ce que phi fait pour être spécial ??
-J'ai vu la "spiral d'or" et comment la faire mais je ne comprend pas en quoi cela représente phi !
-Y'a un aussi quelque chose en rapport avec le nombre d'or (enfin je crois) c'est l'indicatrice d'Euler qui je crois permet de calculer des PGCD, sauf que je n'est pas très bien compris comment ça fonctionner
-encore un dernier truc, j'ai vu la suite de Fibonacci qu'il elle aussi et sensé être en rapport avec ce nombre, mais je ne voi pas lequel !
Voila j'ai cherché sur quelques site... Il y a toujours quelques chose de trop compliqué qui mempêche de continuer !
Merci d'avance !!!!!!!!!!
Cordialement
Charles
J'ai récemment découvert le nombre phi ou le nombre d'or, la solution de l'équation x² -x -1 = 0. Et je me pose pas mal de questions :
-pourquoi ce nombre est-il connu, c'est vrai par exemple avec pi on peut calculer airs et volumes qu'est ce que phi fait pour être spécial ??
-J'ai vu la "spiral d'or" et comment la faire mais je ne comprend pas en quoi cela représente phi !
-Y'a un aussi quelque chose en rapport avec le nombre d'or (enfin je crois) c'est l'indicatrice d'Euler qui je crois permet de calculer des PGCD, sauf que je n'est pas très bien compris comment ça fonctionner
-encore un dernier truc, j'ai vu la suite de Fibonacci qu'il elle aussi et sensé être en rapport avec ce nombre, mais je ne voi pas lequel !
Voila j'ai cherché sur quelques site... Il y a toujours quelques chose de trop compliqué qui mempêche de continuer !
Merci d'avance !!!!!!!!!!
Cordialement
Charles
Salut Chaa 
L'indicatrice d'Euler a pour nom mais ça n'a aucun rapport avec le nombre d'or, que je sache !
mais ça n'a aucun rapport avec le nombre d'or, que je sache !
Le nombre d'or est souvent important en tant que ratio entre deux nombres. Il est symbole d'esthétique en art et est taxé de proportion divine, car si tu mesures les rapports de longueur entre différents membres d'un "beau" corps humain, ou de toute oeuvre naturelle et artistique harmonieuse, t'obtiens le nombre d'or.
Plus spécifiquement, en considérant la suite de Fibonacci :
_{n\in\mathbb{N}}:\mapsto \left\{<br /> \begin{array}<br /> F_1=1 \\<br /> F_2=1 \\<br /> F_{n+2}=F_{n+1}+F_{n}<br /> \end{array})
On s'aperçoit que la limite du ratio vaut
vaut  .
.
En effet, supposons que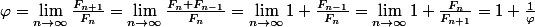 , qui est une autre forme de phi.
, qui est une autre forme de phi.
L'indicatrice d'Euler a pour nom
Le nombre d'or est souvent important en tant que ratio entre deux nombres. Il est symbole d'esthétique en art et est taxé de proportion divine, car si tu mesures les rapports de longueur entre différents membres d'un "beau" corps humain, ou de toute oeuvre naturelle et artistique harmonieuse, t'obtiens le nombre d'or.
Plus spécifiquement, en considérant la suite de Fibonacci :
On s'aperçoit que la limite du ratio
En effet, supposons que
Merci de cette réponse rapide !
Comment tu peux calculer le ratio d'une spirale (de la spiral d'or) ou même un ratio tout simple ????
Pour Fibonacci a quoi sert la formule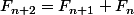 ? Car si je connais juste les premier terme ça ne sert a rien de calculer les deux prochain termes il vaut mieux calculer le n ieme terme non ??
? Car si je connais juste les premier terme ça ne sert a rien de calculer les deux prochain termes il vaut mieux calculer le n ieme terme non ??
pour la limite de cela veux dire que plus n est grand plus la valeur de phi sera exact c'est ca ? Je n'est pas encore les notions des "limites" mais je pense (a toi de me dire si c'est vrai)
cela veux dire que plus n est grand plus la valeur de phi sera exact c'est ca ? Je n'est pas encore les notions des "limites" mais je pense (a toi de me dire si c'est vrai)
qu'on pourrait alors dire que = phi ?
= phi ?
Merci d'avance !!!!!
Comment tu peux calculer le ratio d'une spirale (de la spiral d'or) ou même un ratio tout simple ????
Pour Fibonacci a quoi sert la formule
pour la limite de
qu'on pourrait alors dire que
Merci d'avance !!!!!
chaa13 a écrit:Merci de cette réponse rapide !
Comment tu peux calculer le ratio d'une spirale (de la spiral d'or) ou même un ratio tout simple ????
Pour Fibonacci a quoi sert la formule? Car si je connais juste les premier terme ça ne sert a rien de calculer les deux prochain termes il vaut mieux calculer le n ieme terme non ??
pour la limite decela veux dire que plus n est grand plus la valeur de phi sera exact c'est ca ? Je n'est pas encore les notions des "limites" mais je pense (a toi de me dire si c'est vrai)
qu'on pourrait alors dire que= phi ?
Merci d'avance !!!!!
Salut
Un résultat étonnant
soit la suite de Fibonacci
F(0)=0
F(1)=1
F(2)=1
F(3)=2
F(4)=3
F(n)=F(n-1)+F(n-2)
On peut démontrer F(n)=
On reconnait le nombre d'or
Pour n'importe quelle valeur de l'entier naturel n, cette expression à première vue compliquée désigne donc un nombre entier
Un autre moyen de faire apparaître la suite de Fibonacci et d'écrire sous la forme d'une fraction le nombre 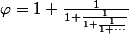 Si on s'arrête à la n-ième étape, on définit une suite
Si on s'arrête à la n-ième étape, on définit une suite  dont le terme général est égal au rapport de deux nombres de Fibonacci successifs
dont le terme général est égal au rapport de deux nombres de Fibonacci successifs  . Cela se montre par récurrence.
. Cela se montre par récurrence.
Par passage à la limite, la suite converge vers
converge vers  qui n'est autre que le nombre d'or.
qui n'est autre que le nombre d'or.
Par passage à la limite, la suite
Ouha merci c'est génial j'ai les formule maintenant !!
Par contre comment je peux faire pour faire le rectangle d'or, j'ai vue sur des site de mettre un coté de 1.618... mais bon c'est pas très précis !Y'a pas une méthode plus précise ?
Et pour les ratio comment je peux calculer par exemple le ratio de la spiral (après avoir fais le rectangle d'or) ?? Et le ratio d'un corps humain ???? ça serai intéressant de dénicher phi dans le monde !
J'ai vu sur wikipédia la formule suivante pour x egal n'importe quel nombre positif :
 ^{ 2 } } }{ 2\cdot x }) = Phi
= Phi
étonnant non ? Pourquoi cela ?
@chan75
Quel raisonnement étonnant ???
Merci d'avannnncccee !!!!!
Par contre comment je peux faire pour faire le rectangle d'or, j'ai vue sur des site de mettre un coté de 1.618... mais bon c'est pas très précis !Y'a pas une méthode plus précise ?
Et pour les ratio comment je peux calculer par exemple le ratio de la spiral (après avoir fais le rectangle d'or) ?? Et le ratio d'un corps humain ???? ça serai intéressant de dénicher phi dans le monde !
J'ai vu sur wikipédia la formule suivante pour x egal n'importe quel nombre positif :
étonnant non ? Pourquoi cela ?
@chan75
Quel raisonnement étonnant ???
Merci d'avannnncccee !!!!!
chaa13 a écrit:Ouha merci c'est génial j'ai les formule maintenant !!
Par contre comment je peux faire pour faire le rectangle d'or, j'ai vue sur des site de mettre un coté de 1.618... mais bon c'est pas très précis !Y'a pas une méthode plus précise ?
Et pour les ratio comment je peux calculer par exemple le ratio de la spiral (après avoir fais le rectangle d'or) ?? Et le ratio d'un corps humain ???? ça serai intéressant de dénicher phi dans le monde !
J'ai vu sur wikipédia la formule suivante pour x egal n'importe quel nombre positif := Phi
étonnant non ? Pourquoi cela ?
@chan75
Quel raisonnement étonnant ???
Merci d'avannnncccee !!!!!
Salut
Voici une petite construction
L'unité est le dm
Trace un carré ABCD
Place le milieu I de [AB]
Trace le cercle de centre I qui passe par C. Il coupe la demi-droite[AB) en E
Si tu calcules IC, tu verras que la longueur de AE est le nombre d'or
Tu repars de la figure que je t'ai indiquée pour avoir le rectangle AEFD (appelé rectangle d'or)
puis tu traces les carrés (compas et règle suffisent) dans l'ordre des numéros au centre.
Enfin tu traces les quarts de cercle
[img][IMG]http://img9.imageshack.us/img9/9264/azr.png[/img][/IMG]
Merci je l'ai fais, elle est juste, mais y'a un truc qui va pas ! Je l'ai fais trop bêtement il faut que je comprenne ! Car la je suis parti sur mon moyen mnémotechnique de faire un carré dans un rectangle ... Quelle est le raisonnement pour la faire ??
Peut on lier (Pas la formule directement mais peut être un dérivé) a cette spiral en imaginent que plus on a de n (on associe n au nombre de carré par exemple) plus la valeur de phi sera exact . Plus la spiral tourne plus on a de décimal juste. Le problème c'est qu'on pars directement d'un rectangle d'or faux ! Comment on pourrais faire pour avoir une décimal de plus a chaque quart de cercle ?
(Pas la formule directement mais peut être un dérivé) a cette spiral en imaginent que plus on a de n (on associe n au nombre de carré par exemple) plus la valeur de phi sera exact . Plus la spiral tourne plus on a de décimal juste. Le problème c'est qu'on pars directement d'un rectangle d'or faux ! Comment on pourrais faire pour avoir une décimal de plus a chaque quart de cercle ?
Désolé je sais que c'est très confus mais je sais pas trop comment posé cette question !
Merci d'avance !!!!!!
Peut on lier
Désolé je sais que c'est très confus mais je sais pas trop comment posé cette question !
Merci d'avance !!!!!!
chaa13 a écrit:Merci je l'ai fais, elle est juste, mais y'a un truc qui va pas ! Je l'ai fais trop bêtement il faut que je comprenne ! Car la je suis parti sur mon moyen mnémotechnique de faire un carré dans un rectangle ... Quelle est le raisonnement pour la faire ??
Peut on lier(Pas la formule directement mais peut être un dérivé) a cette spiral en imaginent que plus on a de n (on associe n au nombre de carré par exemple) plus la valeur de phi sera exact . Plus la spiral tourne plus on a de décimal juste. Le problème c'est qu'on pars directement d'un rectangle d'or faux ! Comment on pourrais faire pour avoir une décimal de plus a chaque quart de cercle ?
Désolé je sais que c'est très confus mais je sais pas trop comment posé cette question !
Merci d'avance !!!!!!
Pour faire le carré n°1, tu traces un arc de cercle de centre B qui passe par E, il coupe [BC] en H.
puis tu traces un arc de cercle de centre C qui passe par B, il coupe [EF] en G.
Tu peux tracer le carré BEGH. Même chose pour la suite.
Sinon, cet ensemble de quarts de cercles n'est pas une vraie spirale.
Tous les rectangles obtenus quand on trace un carré sont des rectangles d'or (Longueur = largeur x nombre d'or)
Il y a un point (un seul) situé àl'intérieur de tous les rectangles. C'est le point d'intersection de (AF) et (CE) qui sont perpendiculaires.
Je crois bien que tu as de quoi faire un exposé sur le nombre d'or :lol3:
chaa13 a écrit:OK merci !!!!
Par rapport au point a lintérieur de "tout", que représente-il ? Si il représente Phi peut on parler justement du lien entre la formuleet ce point ?
Merci d'avance !!!!!!
Ce point est le centre d'une similitude d'angle pi/2 et de rapport 1/phi qui permet de passer d'un rectangle d'or à l'autre (ça a été donné au Bac il y a quelque temps)
46 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

