Nombre premier d'Euler
19 messages
- Page 1 sur 1
Nombre premier d'Euler
Bonjour
Daprès wikipédia :
Nombre premier d'Euler
En théorie des nombres, les nombres premiers d'Euler ou nombres premiers symétriques sont des nombres premiers qui sont à la même distance l'un et l'autre d'un nombre donné. Par exemple 3 et 13 sont tous les deux à 5 unités du nombre 8, donc ils sont des nombres premiers symétriques. Tous les nombres premiers jumeaux sont des nombres premiers symétriques, ainsi que les nombres premiers cousins et les nombres premiers sexy.
Les nombres suivants sont-ils des Nombres premiers dEuler ?
2 et 3 (2,5 ± 0,5)
2 et 5 (3,5 ± 1,5)
2 et 7 (4,5 ± 2,5)
2 et 11 (6,5 ± 4,5)
2 et 13 (7,5 ± 5,5)
Daprès wikipédia :
Nombre premier d'Euler
En théorie des nombres, les nombres premiers d'Euler ou nombres premiers symétriques sont des nombres premiers qui sont à la même distance l'un et l'autre d'un nombre donné. Par exemple 3 et 13 sont tous les deux à 5 unités du nombre 8, donc ils sont des nombres premiers symétriques. Tous les nombres premiers jumeaux sont des nombres premiers symétriques, ainsi que les nombres premiers cousins et les nombres premiers sexy.
Les nombres suivants sont-ils des Nombres premiers dEuler ?
2 et 3 (2,5 ± 0,5)
2 et 5 (3,5 ± 1,5)
2 et 7 (4,5 ± 2,5)
2 et 11 (6,5 ± 4,5)
2 et 13 (7,5 ± 5,5)
Des nombres premier sexy ? Mon dieu !
L'humour des matheux est vraiment à refaire !
Ca me fait penser à un truc d'ailleurs.
C'est l'histoire d'une suite de Cauchy qui décide d'aller à une soirée de l'extrême ! Le thème c'est soirée no-limite ! Donc elle se pointe, et là t'as le videur qui lui, tu déconnes ? C'est pas possible de rentrer. C'est Complet...
Voilà paix à mon âme...
xD
L'humour des matheux est vraiment à refaire !
Ca me fait penser à un truc d'ailleurs.
C'est l'histoire d'une suite de Cauchy qui décide d'aller à une soirée de l'extrême ! Le thème c'est soirée no-limite ! Donc elle se pointe, et là t'as le videur qui lui, tu déconnes ? C'est pas possible de rentrer. C'est Complet...
Voilà paix à mon âme...
xD
Joker62 a écrit:Des nombres premier sexy ? Mon dieu !
L'humour des matheux est vraiment à refaire !
Ca me fait penser à un truc d'ailleurs.
C'est l'histoire d'une suite de Cauchy qui décide d'aller à une soirée de l'extrême ! Le thème c'est soirée no-limite ! Donc elle se pointe, et là t'as le videur qui lui, tu déconnes ? C'est pas possible de rentrer. C'est Complet...
Voilà paix à mon âme...
xD
Salut!
Je n'ai pas tout compris Pourtant, j'adore ce genre d'humour! ^
Daprès wikipédia :
Nombre premier d'Euler
En théorie des nombres, les nombres premiers d'Euler ou nombres premiers symétriques sont des nombres premiers qui sont à la même distance l'un et l'autre d'un nombre donné. Par exemple 3 et 13 sont tous les deux à 5 unités du nombre 8, donc ils sont des nombres premiers symétriques. Tous les nombres premiers jumeaux sont des nombres premiers symétriques, ainsi que les nombres premiers cousins et les nombres premiers sexy.
Les nombres suivants sont-ils des Nombres premiers dEuler ?
Peuvent-ils être symétriques par rapport à un nombre non entier ?
2 et 3 (2,5 ± 0,5)
2 et 5 (3,5 ± 1,5)
2 et 7 (4,5 ± 2,5)
2 et 11 (6,5 ± 4,5)
2 et 13 (7,5 ± 5,5)
Nombre premier d'Euler
En théorie des nombres, les nombres premiers d'Euler ou nombres premiers symétriques sont des nombres premiers qui sont à la même distance l'un et l'autre d'un nombre donné. Par exemple 3 et 13 sont tous les deux à 5 unités du nombre 8, donc ils sont des nombres premiers symétriques. Tous les nombres premiers jumeaux sont des nombres premiers symétriques, ainsi que les nombres premiers cousins et les nombres premiers sexy.
Les nombres suivants sont-ils des Nombres premiers dEuler ?
Peuvent-ils être symétriques par rapport à un nombre non entier ?
2 et 3 (2,5 ± 0,5)
2 et 5 (3,5 ± 1,5)
2 et 7 (4,5 ± 2,5)
2 et 11 (6,5 ± 4,5)
2 et 13 (7,5 ± 5,5)
Ah , on recommence :we:
Des nombres premier sexy ? Mon dieu !
L'humour des matheux est vraiment à refaire !
Ca me fait penser à un truc d'ailleurs.
C'est l'histoire d'une suite de Cauchy qui décide d'aller à une soirée de l'extrême ! Le thème c'est soirée no-limite ! Donc elle se pointe, et là t'as le videur qui lui, tu déconnes ? C'est pas possible de rentrer. C'est Complet...
Voilà paix à mon âme...
xD
Imod
Copyright : Joker62 : 06/05/2009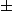 264 jours
264 jours
Des nombres premier sexy ? Mon dieu !
L'humour des matheux est vraiment à refaire !
Ca me fait penser à un truc d'ailleurs.
C'est l'histoire d'une suite de Cauchy qui décide d'aller à une soirée de l'extrême ! Le thème c'est soirée no-limite ! Donc elle se pointe, et là t'as le videur qui lui, tu déconnes ? C'est pas possible de rentrer. C'est Complet...
Voilà paix à mon âme...
xD
Imod
Copyright : Joker62 : 06/05/2009
Bastien L. a écrit:Salut!
Je n'ai pas tout compris Pourtant, j'adore ce genre d'humour! ^
Salut,
j'adore ces blagues de mathematiciens ! (pas facile a replacer par contre)
Pour Bastien: un espace est dit complet si toute suite de Cauchy a une limite.
Joker 62, est ce que tu as d'autres blagues dans ce genre ?
Je me souviens d'une blague raccontee par mon prof de maths de TS:
Exponentielle et logarithme vont en boite. logarithme s'amuse bien mais exponentielle reste dans son coin et ne parle a personne. logarithme lui dit: "viens t'amuser, essaye de t'integrer !" Exponentielle repond: "j'essaye mais ca ne change rien !"
Je ne suis pas sur que ca amuse grand monde ce genre de blagues en fait :we:
Ca n'amuse que la communauté des matheux je pense 
Personnellement je prend énormément mon pieds en lisant les articles de Mathématiques de la désencyclopédie.
http://desencyclopedie.wikia.com/wiki/Cat%C3%A9gorie:Math%C3%A9matique
Personnellement je prend énormément mon pieds en lisant les articles de Mathématiques de la désencyclopédie.
http://desencyclopedie.wikia.com/wiki/Cat%C3%A9gorie:Math%C3%A9matique
Salut!
Merci pour ces précisions! C'est toujours très drôle! :we:
Pour l'histoire avec l'exponentielle, c'est parce-qu'étant donné qu'elle est sa propre primitive on a: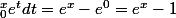 ? C'est ça?
? C'est ça?
Au fait, je crois qu'il n'y a pas sur ce forum de partie exclusivement consacrée à l'humour (mathématique). Ne serait-ce pas possible d'en "intégrer" une pour ne pas mettre des blagues partout ailleurs?
Merci pour ces précisions! C'est toujours très drôle! :we:
Pour l'histoire avec l'exponentielle, c'est parce-qu'étant donné qu'elle est sa propre primitive on a:
Au fait, je crois qu'il n'y a pas sur ce forum de partie exclusivement consacrée à l'humour (mathématique). Ne serait-ce pas possible d'en "intégrer" une pour ne pas mettre des blagues partout ailleurs?
Parce-qu'en fait là ce n'est pas trop sympa pour adrd, on utilise sa discussion mais personne ne lui a répondu
:-S Pour ma part, je ne suis pas plus qualifié que lui, qui es sans-doutes tenté de répondre que les exemples qu'ils donne sont bien à équidistance de deux nombres, mais pas entiers, et que donc ça sort du champ de l'arithmétique
D'ailleurs, si on va par là, ils ont tous cette caractéristique
Bastien L. a écrit: «D'ailleurs, si on va par là, ils ont tous cette caractéristique »
Si on choisit deux nombres premiers impairs, ils ont cette caractéristique car si on additionne deux nombres impairs, on obtient un nombre pair qui est alors divisible par deux. Donc le problème se pose que si on additionne 2 avec un autre nombre premier.
2 est le seul nombre premier pair. Donc, 2 et un autre nombre premier ne pourront pas etre a egale distance d'un entier.
Tous les autres couples de nombres premiers seraient des nombres premiers d'Euler.
Mais, est ce que les nombres premiers d'Euler existent vraiment ? On ne trouve aucune reference sur internet a part cet article wikipedia, et rien du tout en cherchant en anglais, ce qui est quand meme assez surprenant ...
Sinon, pour repondre sur la fonction exponentielle, en fait, par abus de langage, on dit souvent integrer une fonction pour dire en prendre une primitive.
Je ne crois pas qu'une section sur l'humour mathematique se justifie, mais on peut tres bien faire un topic.
Tous les autres couples de nombres premiers seraient des nombres premiers d'Euler.
Mais, est ce que les nombres premiers d'Euler existent vraiment ? On ne trouve aucune reference sur internet a part cet article wikipedia, et rien du tout en cherchant en anglais, ce qui est quand meme assez surprenant ...
Sinon, pour repondre sur la fonction exponentielle, en fait, par abus de langage, on dit souvent integrer une fonction pour dire en prendre une primitive.
Je ne crois pas qu'une section sur l'humour mathematique se justifie, mais on peut tres bien faire un topic.
oui, ça vient toujours du même article wikipedia qui a été effacé. Pour les nombres premiers d'Euler, je n'en sais rien, mais il ne faut pas toujours faire entièrement confiance à wikipedia: http://www.irishtimes.com/newspaper/ireland/2009/0506/1224245992919.html
uztop a écrit:Je ne crois pas qu'une section sur l'humour mathematique se justifie, mais on peut tres bien faire un topic.
Tout à fait d'accord , on a d'ailleurs déjà vu fleurir quelques sujets dans ce style . Sinon l'humour peut très bien se pratiquer au fil des sujets en n'oubliant pas que l'humour n'est pas toujours perçu de la même façon par tout le monde :zen:
Imod
http://pagesperso-orange.fr/jean-paul.davalan/arit/primes/primespatterns.html
http://eljjdx.canalblog.com/tag/Nombres%20premiers
Les nombres premiers d'Euler existent-ils vraiment ?
En tout cas (2;3), (2;5), (2;7), (2;11), (2;13), (3;5), (5;13), (11;17;23;29) sont des constellations de nombres premiers.
http://eljjdx.canalblog.com/tag/Nombres%20premiers
Les nombres premiers d'Euler existent-ils vraiment ?
En tout cas (2;3), (2;5), (2;7), (2;11), (2;13), (3;5), (5;13), (11;17;23;29) sont des constellations de nombres premiers.
http://villemin.gerard.free.fr/Wwwgvmm/Premier/eratoprg.htm#Euler
D'après ce site, les nombres premiers d'Euler seraient les nombres premiers obtenus avec la formule n² + n + 41.
APPLICATION: NOMBRES PREMIERS D'EULER
Recherche de nombres premiers en n² + n + 41 (nombres premiers d'Euler)
D'après ce site, les nombres premiers d'Euler seraient les nombres premiers obtenus avec la formule n² + n + 41.
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
