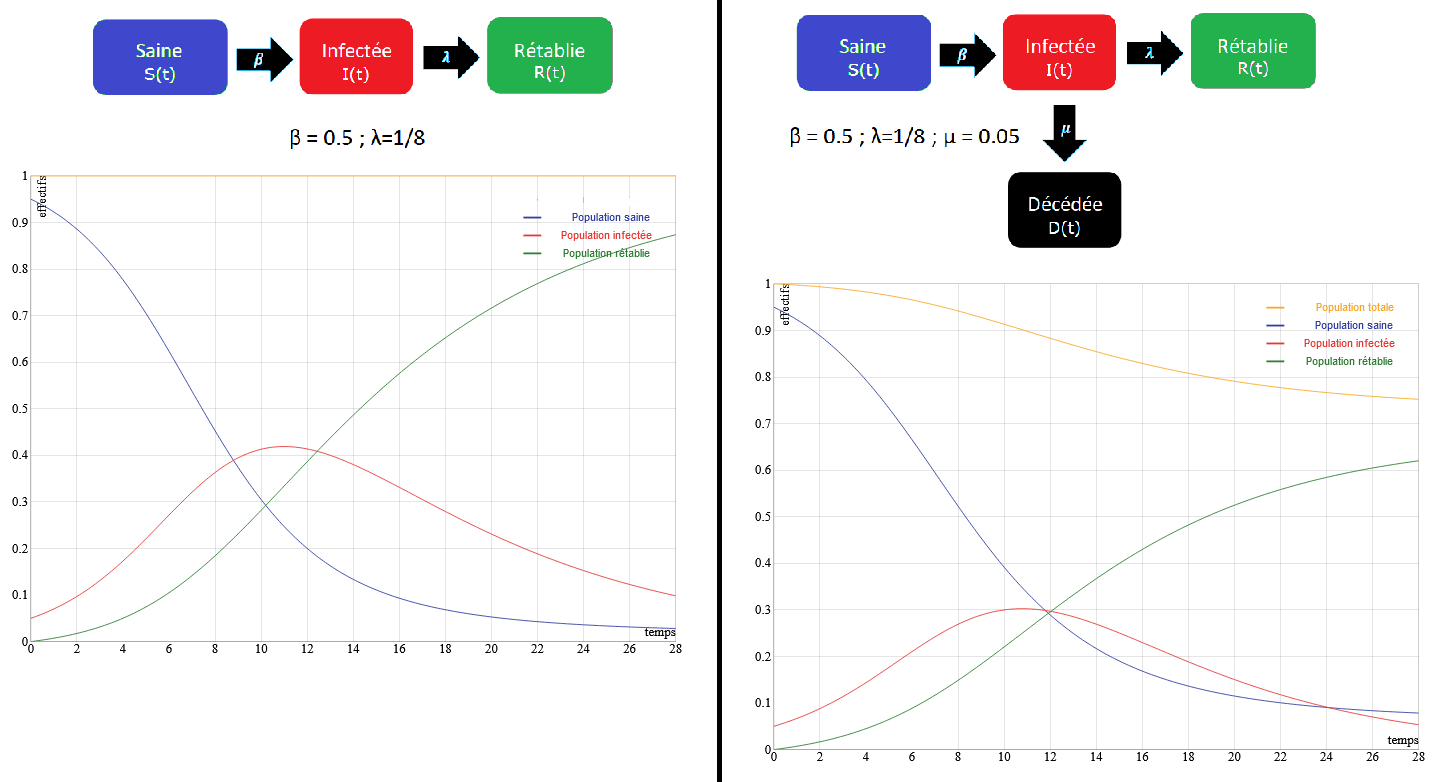
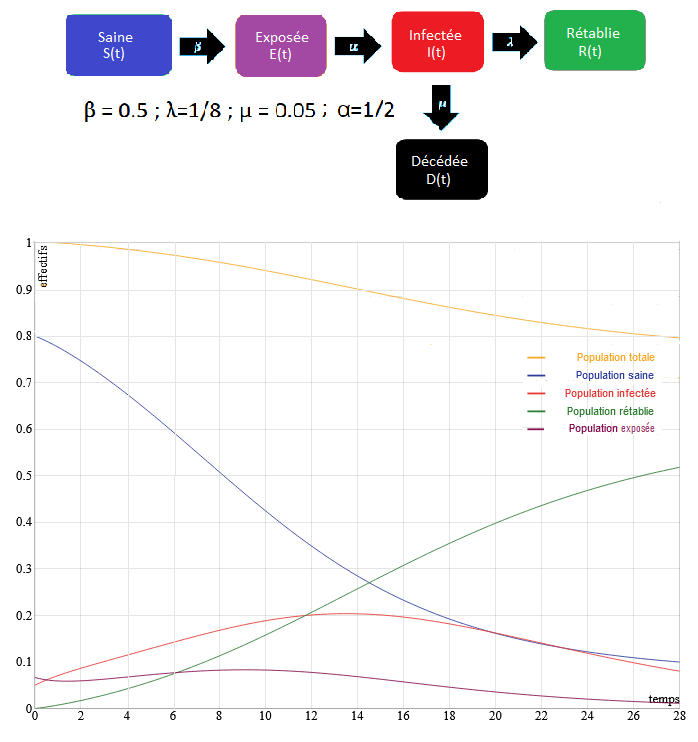
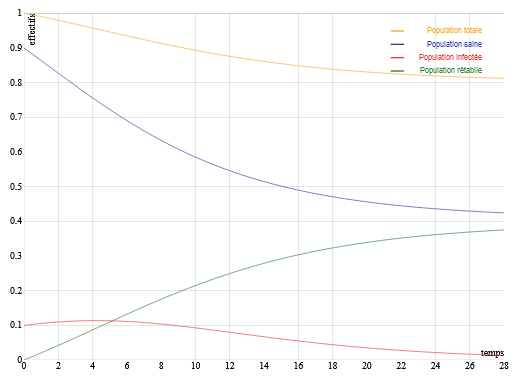
Tant mieux si tu les trouves intéressants, ce sont des modèles assez "simple" mais ils sont quand même une première approche.
Dire que la croissance est exponentielle peut être une bonne approximation au début, lorsque la population est globalement saine mais la croissance finira forcément par se calmer. Même dans la pire épidémie possible, genre invasion de zombies où les infectés ne guérissent pas ; ne meurent pas et continuent à contaminer à grand coup de dents, on aura une croissance logistique.
Pourquoi ? Il y a un plafond, le nombre d'humains à contaminer est fini et pas infini ce qui est nécessaire pour avoir une croissance qui continue d'être exponentielle.
Maintenant, le reste, c'est de la communication, je trouve pas toujours simple de gérer une classe, je ne vais pas donner mon avis pour gérer une population, je ne sais pas faire. Par contre, les modèles mathématiques n'y sont pour rien. Ce ne sont des outils d'aide à la prise à la décision, ils sont aussi précis que possible et ce serait dommage de s'en priver mais il faut les interpréter en prenant du recul sur la situation.
Aucune formule ne donnera la réponse à "comment gérer la crise du covid ?" Faut pas rêver et d'ailleurs même si de nombreux chercheurs ont du faire de superbes modèles bien plus pertinents que ce que je présente, je doute qu'ils aient eu un vrai pouvoir décisionnel dans les choix politiques et c'est normal, chacun son métier.
PS : aucun épidémiologiste digne de ce nom n'a jamais dit "on va tous mourir" du covid, ce serait ridicule devant une maladie qui n'a pas un fort taux de létalité, en revanche beaucoup on dit, la population infectée avec symptômes graves va dépasser les capacités de soins des hôpitaux si on ne fait pas baisser le
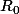
et il me semble que cela s'est produit. On peut décider qu'on s'en fiche et tant pis pour les patients âgés qu'on ne soignera pas mais éthiquement, cela me parait quand même difficile à tenir comme position.