Meilleur manuel de maths?
20 messages
- Page 1 sur 1
Meilleur manuel de maths?
Bonjour,
J'ai 26 ans, je travaille dans les langues mais j'ai envie de me remettre aux maths et à la physique, sachant que j'ai fait un bac L et que j'ai pratiquement tout oublié.
Je voudrais donc reprendre tout le programme à partir de la 6e (je suppose qu'il ne sera pas nécessaire de remonter en arrière, car je sais encore poser des calculs de base !). Auriez-vous des manuels à me conseiller ?
J'ai vu en libraire des manuels de soutien scolaire, mais ils m'ont l'air très succincts (on dirait des résumés de cours alors que je veux les cours détaillés pour bien tout comprendre, d'autant plus que c'est une démarche autonome) et souvent ils reprennent d'autres matières dont je n'ai vraiment pas besoin (histoire géo, anglais etc.).
Pour ce qui est des manuels utilisés au collège, je sais qu'ils sont de qualités très inégales (je me souviens que certains des miens étaient nullissimes), alors je préfère connaître vos avis, car ils coûtent cher ! Merci d'avance pour vos conseils !
J'ai 26 ans, je travaille dans les langues mais j'ai envie de me remettre aux maths et à la physique, sachant que j'ai fait un bac L et que j'ai pratiquement tout oublié.
Je voudrais donc reprendre tout le programme à partir de la 6e (je suppose qu'il ne sera pas nécessaire de remonter en arrière, car je sais encore poser des calculs de base !). Auriez-vous des manuels à me conseiller ?
J'ai vu en libraire des manuels de soutien scolaire, mais ils m'ont l'air très succincts (on dirait des résumés de cours alors que je veux les cours détaillés pour bien tout comprendre, d'autant plus que c'est une démarche autonome) et souvent ils reprennent d'autres matières dont je n'ai vraiment pas besoin (histoire géo, anglais etc.).
Pour ce qui est des manuels utilisés au collège, je sais qu'ils sont de qualités très inégales (je me souviens que certains des miens étaient nullissimes), alors je préfère connaître vos avis, car ils coûtent cher ! Merci d'avance pour vos conseils !
Merci !
En fait je ne me souviens pas du programme, j'ai juste pensé que la 6e serait un bon point de départ, quitte à revoir les évidences. C'est plutôt dans l'autre sens qu'il faut que je fasse attention, car je vise un niveau de licence de maths (sur le long terme évidemment) et je doute qu'un seul bouquin puisse m'amener jusque-là ?
En fait je ne me souviens pas du programme, j'ai juste pensé que la 6e serait un bon point de départ, quitte à revoir les évidences. C'est plutôt dans l'autre sens qu'il faut que je fasse attention, car je vise un niveau de licence de maths (sur le long terme évidemment) et je doute qu'un seul bouquin puisse m'amener jusque-là ?
Euh alors !
Tout ça c'est 6e ?
Une question subsidiaire : est-ce qu'on peut arriver à un niveau en maths ou on comprend réellement pourquoi telle ou telle formule est appliquée (par opposition à du par coeur comme ma prof me le recommandait même en terminale, je me souviens qu'on avait une liste d'une centaine de formules à appliquer et qu'il suffisait de reconnaître dans quel cas il fallait appliquer quoi, sans vraiment comprendre pourquoi) ?
Merci encore pour ton aide !
Aucune idée. Je dirais au pif que linéaire c'est une ligne droite sur un tableau et affine ça fait une courbe parce que y= x+ quelque chose ?Sylviel a écrit:ça c'est certain...
Quelques questions pour situer ton niveau :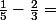
Ca fait 3/15 - 10/15 = -7/15 ?
Euh je suis plus trop sûr ! Même si je fais 2/5 x 2/5 je ne me souviens plus comment multiplier des fractions. 4/25 ?
Je crois que souvenir que ça fait a/b x d/c ?
résouds :
3x-1 = 0 => 3x = 1 donc x = 1/3 ?
1/(2x-1)=2 => euh c'est dur ! 1 = 2(2x-1) donc 1/2=2x-1 donc 1/2+1 = 2x donc x= (1/2+1)/2 ?
(3x-1)(x+2)=0 => x=0 non ?qu'est ce qu'une fonction affine ? linéaire ?
Tout ça c'est 6e ?
Une question subsidiaire : est-ce qu'on peut arriver à un niveau en maths ou on comprend réellement pourquoi telle ou telle formule est appliquée (par opposition à du par coeur comme ma prof me le recommandait même en terminale, je me souviens qu'on avait une liste d'une centaine de formules à appliquer et qu'il suffisait de reconnaître dans quel cas il fallait appliquer quoi, sans vraiment comprendre pourquoi) ?
Merci encore pour ton aide !
Ah zut pour (3x-1)(x+2)=0 en fait je crois avoir été trop vite, sur un souvenir sans doute faux que du moment qu'il y avait un zéro dans une multiplication alors x=0...
Alors : (3x-1)(x+2) = 3x²+6x-x-2=3x²+5x-2
Donc 3x²+5x-2 = 0 =>3x²+5x=2 et là je suis bloqué vu que je ne sais pas comment additionner un x² avec un x.
Alors : (3x-1)(x+2) = 3x²+6x-x-2=3x²+5x-2
Donc 3x²+5x-2 = 0 =>3x²+5x=2 et là je suis bloqué vu que je ne sais pas comment additionner un x² avec un x.
interprete a écrit:Ah zut pour (3x-1)(x+2)=0 en fait je crois avoir été trop vite, sur un souvenir sans doute faux que du moment qu'il y avait un zéro dans une multiplication alors x=0...
Alors : (3x-1)(x+2) = 3x²+6x-x-2=3x²+5x-2
Donc 3x²+5x-2 = 0 =>3x²+5x=2 et là je suis bloqué vu que je ne sais pas comment additionner un x² avec un x.
jreprend juste ca
AB = 0 A = 0 ou B = 0 ... donc 3x-1 = 0 ou x+2=0 ..
sinon cque j'ai survolé avait l'air juste .. en gros c niveau 3éme tout ca
Pour répondre a certaines de tes questions :
- Oui il est nécéssaire que tu comprenne pourquoi tu applique telle ou telle formule quand tu le fais , surtout si tu veut un niveau de licence a terme. Tu risque de changer radicalement de point de vue sur les maths qu'en Term L , je l'espère au moins :lol3:
Sinon, reprendre tout depuis la sixième me semble ... un bonne idée, tu n'as pas grand chose a y perdre car si tu veut acquérir un bon niveau sans limite dans le temps, t'assurer de maîtriser ce que l'on qualifie de basique, élémentaire, c'est déjà quelque chose de fait.
Le mieux pour les cours de maths collège c'est les bouquins scolaires mais ils sont ... très cher pour le peu de temps qu'ils vont te prendre a "torcher" ... en revanche pour ce qui est du lycée, je te conseille dors et déjà :
- Les "prépa bac" Seconde / Première S / Terminale S spé math (10 chacun)
- Le site de Giles Costantini pour la TS
Pour en revenir au collège , si tu veut te passer de livres (je t'y encourage en fait) , une recherche rapide me donne http://fitoussi.serge.free.fr/Classes.htm un site où tu trouve un cours complet pour le collège. Bon maintenant les exercices , tu peut les trouver sur des sites payants genre un allopass=accès pendant 1 semaine, et tu en profite pour faire les copier coller de tout les exercices...
Voilà !
- Oui il est nécéssaire que tu comprenne pourquoi tu applique telle ou telle formule quand tu le fais , surtout si tu veut un niveau de licence a terme. Tu risque de changer radicalement de point de vue sur les maths qu'en Term L , je l'espère au moins :lol3:
Sinon, reprendre tout depuis la sixième me semble ... un bonne idée, tu n'as pas grand chose a y perdre car si tu veut acquérir un bon niveau sans limite dans le temps, t'assurer de maîtriser ce que l'on qualifie de basique, élémentaire, c'est déjà quelque chose de fait.
Le mieux pour les cours de maths collège c'est les bouquins scolaires mais ils sont ... très cher pour le peu de temps qu'ils vont te prendre a "torcher" ... en revanche pour ce qui est du lycée, je te conseille dors et déjà :
- Les "prépa bac" Seconde / Première S / Terminale S spé math (10 chacun)
- Le site de Giles Costantini pour la TS
Pour en revenir au collège , si tu veut te passer de livres (je t'y encourage en fait) , une recherche rapide me donne http://fitoussi.serge.free.fr/Classes.htm un site où tu trouve un cours complet pour le collège. Bon maintenant les exercices , tu peut les trouver sur des sites payants genre un allopass=accès pendant 1 semaine, et tu en profite pour faire les copier coller de tout les exercices...
Voilà !
Merci beaucoup !
En fait j'ai fait le 1er semestre de la TS avant de demander à passer en TL, au vu de mes 4 de moyenne en maths à la fin du premier semestre... j'ai donc vu la fiche d'une centaine de formules que nous avait distribuée la prof (un topo de toutes les formules apprises depuis la 2nde), qui nous a dit de juste les apprendre par coeur, la clé pour le bac étant d'acquérir les "automatismes" en sachant qu'est-ce qu'il faut appliquer quand.
Ta réponse est donc encourageante, car je déteste appliquer sans comprendre. Mais veux-tu dire que je vais devoir attendre le niveau licence pour commencer à comprendre véritablement le "fonctionnement" de toutes ces formules ?
Sinon, un grand merci pour ces tuyaux - pour le collège, c'est vrai que l'internet m'évitera de grosses dépenses. A partir du niveau 2nde je vais quand même acheter, mais j'ai le temps avant de revenir solliciter vos avis !
Merci !
Oui il est nécéssaire que tu comprenne pourquoi tu applique telle ou telle formule quand tu le fais , surtout si tu veut un niveau de licence a terme. Tu risque de changer radicalement de point de vue sur les maths qu'en Term L , je l'espère au moins
En fait j'ai fait le 1er semestre de la TS avant de demander à passer en TL, au vu de mes 4 de moyenne en maths à la fin du premier semestre... j'ai donc vu la fiche d'une centaine de formules que nous avait distribuée la prof (un topo de toutes les formules apprises depuis la 2nde), qui nous a dit de juste les apprendre par coeur, la clé pour le bac étant d'acquérir les "automatismes" en sachant qu'est-ce qu'il faut appliquer quand.
Ta réponse est donc encourageante, car je déteste appliquer sans comprendre. Mais veux-tu dire que je vais devoir attendre le niveau licence pour commencer à comprendre véritablement le "fonctionnement" de toutes ces formules ?
Sinon, un grand merci pour ces tuyaux - pour le collège, c'est vrai que l'internet m'évitera de grosses dépenses. A partir du niveau 2nde je vais quand même acheter, mais j'ai le temps avant de revenir solliciter vos avis !
Merci !
Bon, comme on te l'a dit c'est plutôt niveau 3ème ce que je t'ai donné. (enfin les calculs sur les fractions c'est 5ème). Grosso modo tu peux regarder à partir de la 4ème (de mémoire il n'y a rien en 6ème et 5ème) sur internet.
4ème - 2nde --> comment calculer (fractions, racines, puissance, équations simple, système, un brin de trigo, définition de base d'une fonction...)
1ère - Tale : on commence à voir des outils plus puissant (dérivation, intégrale, ...)
Après le bac : on recommence en étant rigoureux (ou presque) :D
Pour ce qui est de ta question de 'comprendre' pourquoi on applique telle ou telle formule. Oui on peut comprendre, mais pour cela il faut avoir pris du recul sur le cours, et sur les applications. C'est l'expérience qui fait penser à regarder dans telle direction, à voir les indices qui montrent que telle méthode fonctionnera plutôt qu'une autre... On peut t'expliquer sur chaque exos pourquoi tel truc marche et pas tel autre, pas besoin d'arriver en TS ou en Licence pour ça. J'essaie de l'expliquer aux 4ème et 3ème du forum (parfois), où à mes élèves en cours particuliers. Après il y a un moment où 'le génie ne s'explique pas'. Il y a un moment où telle formule fonctionne, et ceux qui l'ont vu auront chacun une explication (ou non d'ailleurs) différente... Et une bonne part d'entre elle sont du type : j'ai déjà vu ce genre de problème, et j'avais réussi ainsi.
Hésite pas à venir poser des questions sur les forums, et éventuellement à suivre les exos qui sont posés pour voir si tu y arrives, et si tu trouves la même chose que le correcteur. Quand tu te sentiras plus confiant tu pourras répondre (expliquer quelque chose c'est le meilleur moyen de le comprendre...).
Bon courage à toi !
4ème - 2nde --> comment calculer (fractions, racines, puissance, équations simple, système, un brin de trigo, définition de base d'une fonction...)
1ère - Tale : on commence à voir des outils plus puissant (dérivation, intégrale, ...)
Après le bac : on recommence en étant rigoureux (ou presque) :D
Pour ce qui est de ta question de 'comprendre' pourquoi on applique telle ou telle formule. Oui on peut comprendre, mais pour cela il faut avoir pris du recul sur le cours, et sur les applications. C'est l'expérience qui fait penser à regarder dans telle direction, à voir les indices qui montrent que telle méthode fonctionnera plutôt qu'une autre... On peut t'expliquer sur chaque exos pourquoi tel truc marche et pas tel autre, pas besoin d'arriver en TS ou en Licence pour ça. J'essaie de l'expliquer aux 4ème et 3ème du forum (parfois), où à mes élèves en cours particuliers. Après il y a un moment où 'le génie ne s'explique pas'. Il y a un moment où telle formule fonctionne, et ceux qui l'ont vu auront chacun une explication (ou non d'ailleurs) différente... Et une bonne part d'entre elle sont du type : j'ai déjà vu ce genre de problème, et j'avais réussi ainsi.
Hésite pas à venir poser des questions sur les forums, et éventuellement à suivre les exos qui sont posés pour voir si tu y arrives, et si tu trouves la même chose que le correcteur. Quand tu te sentiras plus confiant tu pourras répondre (expliquer quelque chose c'est le meilleur moyen de le comprendre...).
Bon courage à toi !
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re,
Sylviel a parfaitement répondu pour la "compréhension" des maths. De toute façon, sans rien comprendre on ne vas pas loin, c'est certain.
Sinon, pour les cours de 6ème à 3ème tout y est sur le site que je t'ai passé. Je te conseille de lire les cours niveau 6/5 ème au moins même si tu veut faire les exercices de niveau 4ème .
Autre chose : Combien d'heures ( par semaine) compte tu investir ?
Sylviel a parfaitement répondu pour la "compréhension" des maths. De toute façon, sans rien comprendre on ne vas pas loin, c'est certain.
Sinon, pour les cours de 6ème à 3ème tout y est sur le site que je t'ai passé. Je te conseille de lire les cours niveau 6/5 ème au moins même si tu veut faire les exercices de niveau 4ème .
Autre chose : Combien d'heures ( par semaine) compte tu investir ?
Re-merci à tous pour vos contributions, ça m'aide beaucoup, car ça fait un certain temps que j'y songe et que je galère sur Amazon et Cie à me demander ce que je dois me prendre.
Le lien m'a l'air très complet, je suis déjà en train de lire le manuel de 6e. Je viens également de découvrir le manuel "Sésamath" téléchargeable gratuitement. Mais je ne sais pas encore ce qu'il vaut.
Je travaille comme interprète de conférence, du coup je bosse 10 jours par mois à tout casser - je suis censé préparer mes conférences le reste du temps, mais comme je fais rarement du technique, on peut dire que je suis en vacances 20 jours par mois, d'où mon intérêt pour les maths et la physique. Du coup je peux y passer disons 3/4h par jour pendant 20 jours par mois... et j'ai la flemme de calculer combien d'heures ça fait par mois en moyenne, me voilà bien parti !
Le lien m'a l'air très complet, je suis déjà en train de lire le manuel de 6e. Je viens également de découvrir le manuel "Sésamath" téléchargeable gratuitement. Mais je ne sais pas encore ce qu'il vaut.
Je travaille comme interprète de conférence, du coup je bosse 10 jours par mois à tout casser - je suis censé préparer mes conférences le reste du temps, mais comme je fais rarement du technique, on peut dire que je suis en vacances 20 jours par mois, d'où mon intérêt pour les maths et la physique. Du coup je peux y passer disons 3/4h par jour pendant 20 jours par mois... et j'ai la flemme de calculer combien d'heures ça fait par mois en moyenne, me voilà bien parti !
interprete a écrit:Re-merci à tous pour vos contributions, ça m'aide beaucoup, car ça fait un certain temps que j'y songe et que je galère sur Amazon et Cie à me demander ce que je dois me prendre.
Le lien m'a l'air très complet, je suis déjà en train de lire le manuel de 6e. Je viens également de découvrir le manuel "Sésamath" téléchargeable gratuitement. Mais je ne sais pas encore ce qu'il vaut.
Je vais voir ...
interprete a écrit:Je travaille comme interprète de conférence, du coup je bosse 10 jours par mois à tout casser - je suis censé préparer mes conférences le reste du temps, mais comme je fais rarement du technique, on peut dire que je suis en vacances 20 jours par mois, d'où mon intérêt pour les maths et la physique. Du coup je peux y passer disons 3/4h par jour pendant 20 jours par mois... et j'ai la flemme de calculer combien d'heures ça fait par mois en moyenne, me voilà bien parti !
Exercice préliminaire. Calcule moi ça :ptdr:
Bon, alors si tu peut investir 2h par jour en math ( puis le reste pour la physique) 20 jours par mois, c'est pas mal pour quelqu'un qui bosse :we:
PS. Bon, j'ai regardé les Sésamath, prends bien les sésamath et pas les math en poche, les sésamath sont pas mauvais je trouve.
Allez, au boulot, premier chapitre !!
Moi je ne suis pas (du tout) fan des manuels sésamath, surtout pour une utilisation en autodidacte. Ils sont conformes à l'approche constructiviste, suivant laquelle les élèves doivent tout découvrir par eux-memes, tout (en particulier toutes les démonstrations) est fait dans les activités, qui sont trop nombreuses pour pouvoir être toutes faites en classe à mon avis, il n'y a pas de cours à proprement parler mais seulement une liste de « méthodes et notions essentielles », c'est utile pour savoir comment faire telle ou telle chose, mais pas rigoureux mathématiquement: les notions étudiées ne sont pas toujours définies, il n'y a pas toujours de distinction claire entre définition et propriété (c'est seulement écrit « à connaitre »), si une propriété a été démontrée dans une activité ce n'est pas indiqué, autrement dit le cours se résume à une liste de recettes.
Par exemple, je suis devant le manuel de 3e, chapitre N7: Notion de fonction. Les activités parlent d'exprimer des choses « en fonction » d'autres choses, à chaque fois le problème est plus ou moins concret, la variable est une grandeur identifiable (distance, vitesse), puis dans le cours on parle de fonction de façon détachée de tout contexte, de courbe d'une fonction, on indique sur des exemples comment trouver l'image, les antécédents avec un tableau, une courbe, une formule... Mais les notions de fonction, de courbe d'une fonction, d'image, d'antécédent ne sont pas définies, on en donne seulement des exemples. Le chapitre suivant sur les fonctions linéaires et affines me semble mieux, on définit ces fonctions et aussi la représentation graphique (ce qui aurait du être fait au chapitre précédent).
Autre exemple, dans le manuel de 5e, le cours du chapitre sur le parallélogramme ne rappelle pas la définition d'un parallélogramme, mais seulement comment le construire. Dans l'édition 2006, deux définitions possibles étaient citées dans l'activité 2, qui proposait de montrer leur équivalence, mais ne montrait en fait qu'une implication, la « démonstration » de l'autre implication se limitant à « Les quadrilatères ci-dessus semblent-ils avoir un centre de symétrie? Si oui, où se situe-t-il? Recopie puis complète la phrase suivante: « Si un quadrilatère a ses cotés opposés parallèles deux à deux alors il a ...». ». Cette activité a été supprimée dans l'édition 2010 mais le parallélogramme n'est pas davantage défini (il est dans le lexique). Les méthodes et notions essentielles utilisent des propriétés des parallélogrammes, mais ces propriétés ne sont pas écrites noir sur blanc dans le cours.
En 6e, on ne définit pas les angles aigus, obtus ou droits dans le chapitre sur les angles, avant de donner des exercices utilisant ces notions, et le chapitre sur les angles droits n'en rappelle pas la définition (donnée dans une activité du chapitre sur les angles), on explique comment construire la perpendiculaire à une droite passant par un point mais on ne définit pas les droites perpendiculaires. Ces définitions sont uniquement dans le lexique en fin de livre.
Je ne vais pas détailler tous les chapitres de tous les livres comme ça, mais en résumé si on utilise ces manuels je pense qu'il vaut mieux avoir un prof derrière qui sélectionne les activités et exercices à faire et fait un vrai cours, mais tu peux toujours les utiliser pour les exercices corrigés. Ça ne vaut à mon avis pas le coup d'acheter des manuels de collège ou lycée neufs, mais si tu préfères des manuels papier aux cours disponibles sur internet et que tu habites en région parisienne on en trouve d'occasion pour quelques euros chez Boulinier.
Par exemple, je suis devant le manuel de 3e, chapitre N7: Notion de fonction. Les activités parlent d'exprimer des choses « en fonction » d'autres choses, à chaque fois le problème est plus ou moins concret, la variable est une grandeur identifiable (distance, vitesse), puis dans le cours on parle de fonction de façon détachée de tout contexte, de courbe d'une fonction, on indique sur des exemples comment trouver l'image, les antécédents avec un tableau, une courbe, une formule... Mais les notions de fonction, de courbe d'une fonction, d'image, d'antécédent ne sont pas définies, on en donne seulement des exemples. Le chapitre suivant sur les fonctions linéaires et affines me semble mieux, on définit ces fonctions et aussi la représentation graphique (ce qui aurait du être fait au chapitre précédent).
Autre exemple, dans le manuel de 5e, le cours du chapitre sur le parallélogramme ne rappelle pas la définition d'un parallélogramme, mais seulement comment le construire. Dans l'édition 2006, deux définitions possibles étaient citées dans l'activité 2, qui proposait de montrer leur équivalence, mais ne montrait en fait qu'une implication, la « démonstration » de l'autre implication se limitant à « Les quadrilatères ci-dessus semblent-ils avoir un centre de symétrie? Si oui, où se situe-t-il? Recopie puis complète la phrase suivante: « Si un quadrilatère a ses cotés opposés parallèles deux à deux alors il a ...». ». Cette activité a été supprimée dans l'édition 2010 mais le parallélogramme n'est pas davantage défini (il est dans le lexique). Les méthodes et notions essentielles utilisent des propriétés des parallélogrammes, mais ces propriétés ne sont pas écrites noir sur blanc dans le cours.
En 6e, on ne définit pas les angles aigus, obtus ou droits dans le chapitre sur les angles, avant de donner des exercices utilisant ces notions, et le chapitre sur les angles droits n'en rappelle pas la définition (donnée dans une activité du chapitre sur les angles), on explique comment construire la perpendiculaire à une droite passant par un point mais on ne définit pas les droites perpendiculaires. Ces définitions sont uniquement dans le lexique en fin de livre.
Je ne vais pas détailler tous les chapitres de tous les livres comme ça, mais en résumé si on utilise ces manuels je pense qu'il vaut mieux avoir un prof derrière qui sélectionne les activités et exercices à faire et fait un vrai cours, mais tu peux toujours les utiliser pour les exercices corrigés. Ça ne vaut à mon avis pas le coup d'acheter des manuels de collège ou lycée neufs, mais si tu préfères des manuels papier aux cours disponibles sur internet et que tu habites en région parisienne on en trouve d'occasion pour quelques euros chez Boulinier.
Merci beaucoup pour ces précisions !
Entre-temps je suis allé chez Gibert, et j'ai trouvé "Les maths au collège - démontrer pour comprendre", d'Alexandre Casamayou et François Pantigny. Il est censé couvrir tout le programme de 5e, 4e et 3e. Je n'ai pu que le feuilleter très rapidement, il n'a pas l'air trop mal (mais je n'ai rien lu en détail). Chez Ellipses pour 16 euros neuf...
Entre-temps je suis allé chez Gibert, et j'ai trouvé "Les maths au collège - démontrer pour comprendre", d'Alexandre Casamayou et François Pantigny. Il est censé couvrir tout le programme de 5e, 4e et 3e. Je n'ai pu que le feuilleter très rapidement, il n'a pas l'air trop mal (mais je n'ai rien lu en détail). Chez Ellipses pour 16 euros neuf...
interprete a écrit:Bonjour,
J'ai 26 ans, je travaille dans les langues mais j'ai envie de me remettre aux maths et à la physique, sachant que j'ai fait un bac L et que j'ai pratiquement tout oublié.
Je voudrais donc reprendre tout le programme à partir de la 6e (je suppose qu'il ne sera pas nécessaire de remonter en arrière, car je sais encore poser des calculs de base !). Auriez-vous des manuels à me conseiller ?
J'ai vu en libraire des manuels de soutien scolaire, mais ils m'ont l'air très succincts (on dirait des résumés de cours alors que je veux les cours détaillés pour bien tout comprendre, d'autant plus que c'est une démarche autonome) et souvent ils reprennent d'autres matières dont je n'ai vraiment pas besoin (histoire géo, anglais etc.).
Pour ce qui est des manuels utilisés au collège, je sais qu'ils sont de qualités très inégales (je me souviens que certains des miens étaient nullissimes), alors je préfère connaître vos avis, car ils coûtent cher ! Merci d'avance pour vos conseils !
Bonjour
Ou en êtes vous actuellement dans vos recherches ? Avez-vous commencer votre apprentissage ?
Le livre de collège que tu mentionnes a l'air bien d'après sa description mais je ne l'ai jamais vu, j'essaierai d'y jeter un coup d'oeil si j'y pense quand j'irai à Gibert.
Sinon, j'ai regardé ce qu'il y avait comme livres spécialement conçus pour la remise à niveau des adultes. J'ai trouvé une série en 3 tomes Les bases de l'algèbre (niveau collège et seconde), Les bases de la géométrie (toute la géométrie de la 6e à la TS, et aussi les nombres complexes et une introduction aux matrices) et Les bases de l'analyse (1e S et TS), écrite par des profs du CNAM (et de collège et lycée pour le premier tome), qui couvre tout le programme de la 6e à la TS. C'est conçu pour de l'autoformation, avec le cours, puis les exercices corrigés, et le lecteur est censé tout traiter dans l'ordre. Je pense qu'il y a moins d'exercices dans cette série que dans le livre que tu mentionnes (mais il faut tous les faire et ils sont tous corrigés).
Il y a aussi des livres de préparation aux concours de la fonction publique de catégorie B et C qui seraient peut-être intéressants, mais je ne les ai pas regardés, je le ferai aussi quand j'irai à Gibert si j'y pense.
Sinon, j'ai regardé ce qu'il y avait comme livres spécialement conçus pour la remise à niveau des adultes. J'ai trouvé une série en 3 tomes Les bases de l'algèbre (niveau collège et seconde), Les bases de la géométrie (toute la géométrie de la 6e à la TS, et aussi les nombres complexes et une introduction aux matrices) et Les bases de l'analyse (1e S et TS), écrite par des profs du CNAM (et de collège et lycée pour le premier tome), qui couvre tout le programme de la 6e à la TS. C'est conçu pour de l'autoformation, avec le cours, puis les exercices corrigés, et le lecteur est censé tout traiter dans l'ordre. Je pense qu'il y a moins d'exercices dans cette série que dans le livre que tu mentionnes (mais il faut tous les faire et ils sont tous corrigés).
Il y a aussi des livres de préparation aux concours de la fonction publique de catégorie B et C qui seraient peut-être intéressants, mais je ne les ai pas regardés, je le ferai aussi quand j'irai à Gibert si j'y pense.
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
