Je suis en train de modéliser des engrenages sur un logiciel de conception 3D mais je rencontre le problème suivant :
(Pour une meilleur compréhension j'ai joint des images représentant mon problème)
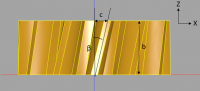
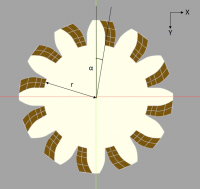
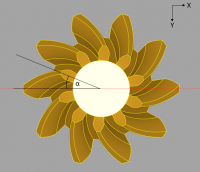
J'aimerai calculer pour un angle d'hélice donné Beta l'angle alpha associé. Je précise que je dispose des valeurs de toutes les distances qui pourraient être intéressantes (c.f. les rayons, l'épaisseur des dents 'b', etc.)
Une de mes premières idées pour l'engrenage cylindrique était de poser :
tan(beta) = c / b
avec :
c = sin(alpha) * r
Cependant ceci me limite à c <= r, ce qui limite l'angle beta, j'en déduis donc que cette méthode n'est pas la bonne.
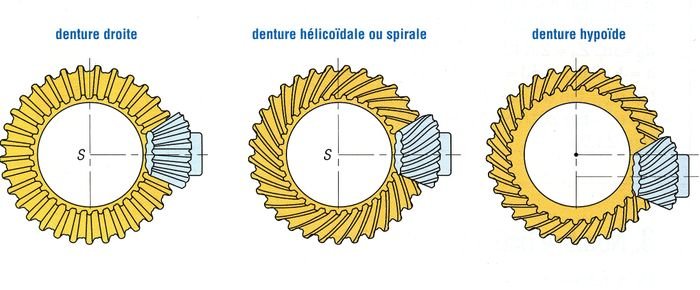
Si vous avez des idées d'abord pour l'engrenage cylindrique et puis pour l'engrenage conique (qui apporte un peu plus de complexité) je suis à l'écoute !
Merci