Exo+Bonnus
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 21:19
par nada-top » 29 Aoû 2006, 21:19
[FONT=Palatino Linotype]
ni hao [/FONT] :lol3:
voilà un petit
exo sympa :
soient
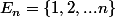
;
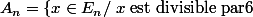
et
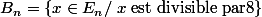
* calculer :
}{card(E_n)})
et voilà le petit
bonnus :
résoudre dans
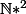
l'équation suivante :
^{x!} = (x!)^{y!})
et pour finir voici un
indice trés utile :
Bonne chance :ptdr:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 29 Aoû 2006, 22:53
par aviateurpilot » 29 Aoû 2006, 22:53
on pose
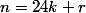
avec

}{card(E_n)}=\lim_{n\to +\infty}\frac{[n/6]+[n/8]-[n/24]}{n}=\lim_{k\to +\infty}\frac{4k+r/6+3k+r/8-k-r/24}{24k+r}=\lim_{n\to +\infty}\frac{6k+r/4}{24k+r})
donc
}{card(E_n)}\le \lim_{k\to +\infty}\frac{6k+23/4}{24k}=\frac{6}{24}=\frac{1}{4})
donc
}{card(E_n)}=\frac{1}{4})
sauf erreur
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 29 Aoû 2006, 23:05
par aviateurpilot » 29 Aoû 2006, 23:05
^{x!}=x!^{y!})
il est clair que
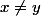
=> si
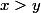
^{x!}>(x!+1)^{y!}>x!^{y!})
=> si
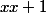
tel que

donc
^{x!}=(x!^{x!})^k)
donc
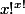
divise
^{x!})
donc
^{x!})=x!^{x!})
or on a
^{x!})=PGCD(x!,x!+1)^{x!}=1)
^
par suite
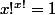
=>

ou

on verfie que

n'ai pas une solution (0 n'appartient pas à
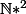
)
donc il n'existe pas de solution de
^{x!}=x!^{y!})
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 23:14
par nada-top » 29 Aoû 2006, 23:14
bonsoir,
oui c'est juste aviateurpilot , à part que tu voulais surement dire
}{card(E_n)}=..)
on peut aussi appliquer le theorème des gendarmes en remarquons :
}{card(E_n)} < \frac{1}{4}+\frac{1}{n})
on a
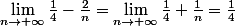
d'ou on conclut.:lol3:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 29 Aoû 2006, 23:19
par aviateurpilot » 29 Aoû 2006, 23:19
et pour le petit bonnus
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 23:25
par nada-top » 29 Aoû 2006, 23:25
Ah je vois que tu as modifié ta 1ère réponse donc le principe est le meme c'est le TG. :++:
sinon pour le bonnus c'est correct aussi :we: , il n'y a pas de solutions mais je vais d'abord analyser ta répopnse car j'ai pas encore vu d'arithmétique .
ceci dit il y a plus simple :lol4:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 23:48
par nada-top » 29 Aoû 2006, 23:48
Re,
aviateurpilot a écrit:^{x!}) = PGCD(x! , (x!+1))^{x!} = 1)
je comprend pourquoi c'est égale 1 car ce sont des nombres consécutifs mais je comprends pas pourquoi
^{x!}) = PGCD(x! , (x!+1))^{x!})
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 29 Aoû 2006, 23:52
par aviateurpilot » 29 Aoû 2006, 23:52
si
=d)
alors
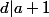
et
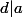
donc
-a)
par suit
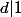
donc
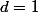
tu sais que
=(pgcd(a,b))^n)
non?
N.B:
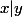
c-à-dire

divise

.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 29 Aoû 2006, 23:58
par nada-top » 29 Aoû 2006, 23:58
oui oui j'ai compris pourquoi c'est égale à 1 mais ma question était à propos de :
 = pgcd(a,b)^n)
, c'est une propriété ??
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 30 Aoû 2006, 00:04
par aviateurpilot » 30 Aoû 2006, 00:04
oui,c'est une propriété.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 30 Aoû 2006, 00:11
par nada-top » 30 Aoû 2006, 00:11
ok merci je vais chercher comment ça se démontre en tous cas pour le bonnus il suffisait de voir que : si
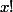
est
pair alors
^{x!})
est
impair or
^{y!})
est
pair donc il n'y a pas de solution.
bonne soirée :lol3:
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 30 Aoû 2006, 00:20
par BancH » 30 Aoû 2006, 00:20
C'est facile à comprendre:
Si on a
=k)
alors
^2=PGCD(a^2k^2,b^2k^2)=k^2)
PS: Pourquoi travailler dans
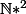
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 30 Aoû 2006, 00:27
par aviateurpilot » 30 Aoû 2006, 00:27
tu veux dire
si

, on verifie que c'est pas une solution
si
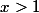
,
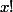
est pair ......
c'est bien,
et pour ma 1er solution.
je voulais dire:
il est clair que
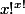
divise
^{x!})
ce qui est absurde
donc pas de solution
mais je me suis dit que cela ne peux pas etre clair pour tout le monde :we:
alors j'ai fait grandir la solution {lol}
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 30 Aoû 2006, 00:33
par aviateurpilot » 30 Aoû 2006, 00:33
oui banch
ce que tu dis est vrai
mais nada-top parle de
)^n=PGCD(a^n,b^n))
et pour
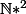
c'est parce qu'il utilisé
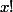
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 30 Aoû 2006, 08:56
par nada-top » 30 Aoû 2006, 08:56
Bonjour,
aviateurpilot a écrit:tu veux dire
si ,

on verifie que c'est pas une solution
si ,
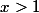
est pair ......
oui c'est ça , je devais partir donc j'ai écrit à la hâte.
aviateurpilot a écrit:mais je me suis dit que cela ne peux pas etre clair pour tout le monde
alors j'ai fait grandir la solution {lol}
peu importe la longueur tant qu'il y a une diversité :lol3:
>> Banch : je crois que t'as eu la réponse et merci pour les précisions.
@+
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
divise
on verifie que c'est pas une solution
est pair ......