Equation du type a^b=b.m
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 21 Sep 2016, 20:59
par anthony_unac » 21 Sep 2016, 20:59
Bonsoir,
Une petite recherche personnelle m'a conduit vers deux équations que je peine à résoudre :
1/
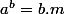
avec

un entier naturel,

une entier naturel,

un entier naturel impair et

Comment résoudre cette 1ere équation en fonction de

et

:
Pour ma part je trouve une solution évidente

et une solution plus raffinée à tâton :
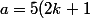)
et
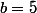
N'hésitez pas à me contredire si je me perds
-
bolza
- Membre Relatif
- Messages: 449
- Enregistré le: 04 Juin 2015, 10:15
-
 par bolza » 21 Sep 2016, 21:06
par bolza » 21 Sep 2016, 21:06
Bonjour,
b divise a^b <=> b divise a...
donc en particulier, l'exemple que tu as donné est bon

EDIT j'ai peut être été un peu vite : b divise a => b divise a^b, la réciproque peut être pas..
par exemple si b=15² et a=15 alors a^b = 15^225 = b*15^223...

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 21 Sep 2016, 21:15
par anthony_unac » 21 Sep 2016, 21:15
Si je comprends bien votre réponse, une solution du type
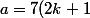)
et
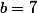
aurait été tout aussi satisfaisante tout comme (de façon générale)
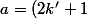(2k+1))
et

-
bolza
- Membre Relatif
- Messages: 449
- Enregistré le: 04 Juin 2015, 10:15
-
 par bolza » 21 Sep 2016, 21:21
par bolza » 21 Sep 2016, 21:21
oui, en fait de manière générale, tous les facteurs premiers de b doivent être des facteur premiers de a.
ce qui est évidemment le cas si b divise a.

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 21 Sep 2016, 21:27
par anthony_unac » 21 Sep 2016, 21:27
Merci pour cette précision, voici à présent la 2eme équation (encore plus pourrie) :
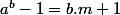
avec

,

,

entiers naturels
On cherche tous les couples
)
vérifiant cette égalité.
-
bolza
- Membre Relatif
- Messages: 449
- Enregistré le: 04 Juin 2015, 10:15
-
 par bolza » 21 Sep 2016, 21:45
par bolza » 21 Sep 2016, 21:45
oui alors là ça me semble effectivement plus délicat ^^'
en gros on cherche a et b tel que a^b soit congru à 2 modulo b
déjà pour a fixé, trouvé un k tel que a^k =2 (mod b) est un problème assez difficile en soi
(car c'est un calcul de logarithme discret)
mais on peut peut-être trouver quelque chose en exploitant le petit théorème de Fermat :
si b est premier, et si a est premier avec b, alors a^b=a (mod b)
donc si de plus a=2 (mod b) c'est gagné, par exemple :
b=5, a=7
alors 7^5=16807=2(mod 5)
en particulier : 7^5 = 5*3361 +2 et donc 7^5-1 = 5*3361+1.
donc les couples de la forme (b,a) avec b=p (p un nombre premier impair) et a=kp+2 sont des solutions,
mais le cas général reste compliqué je pense ^^'
Modifié en dernier par
bolza le 21 Sep 2016, 22:12, modifié 2 fois.

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 21 Sep 2016, 22:01
par anthony_unac » 21 Sep 2016, 22:01
Merci pour toutes ces infos

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités