Dénombrement
14 messages
- Page 1 sur 1
Dénombrement
Salut . J ai un souci . Ça me fera vraiment très plaisir de trouver une solution à ce problème.
Une urne contient 6boules portant le numéro 1 , 4 boules portant le numéro √3,5boules portant le numéro -1 et 5 boules portant le numéro -√3 toutes indiscernables au toucher . on tire successivement et sans remise deux boules de l urne . On désigne par a le nombre porté par la première boule et par b celui porté par la deuxième boule . On considère deux points fixes et distincts A et B du plan et l équation (E): acosx+bsinx=0.
1) Déterminer le nombre de tirages que l on peut effectuer pour que -π/4 soit solution de (E).
2) Détermine le nombre de tirages que l on peut effectuer pour que le vecteur aMA+bMB soit constant pour tout point M du plan.
3) Déterminer le nombre de tirages que l on peut effectuer pour que π/3 soit solution de (E).
Merci pour l attention
Une urne contient 6boules portant le numéro 1 , 4 boules portant le numéro √3,5boules portant le numéro -1 et 5 boules portant le numéro -√3 toutes indiscernables au toucher . on tire successivement et sans remise deux boules de l urne . On désigne par a le nombre porté par la première boule et par b celui porté par la deuxième boule . On considère deux points fixes et distincts A et B du plan et l équation (E): acosx+bsinx=0.
1) Déterminer le nombre de tirages que l on peut effectuer pour que -π/4 soit solution de (E).
2) Détermine le nombre de tirages que l on peut effectuer pour que le vecteur aMA+bMB soit constant pour tout point M du plan.
3) Déterminer le nombre de tirages que l on peut effectuer pour que π/3 soit solution de (E).
Merci pour l attention
Re: Dénombrement
Bonjour,
Quel est exactement ton souci ? Qu'as-tu essayé ?
Pour la 1) : quel est le cosinus et le sinus de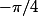 ? Quels sont les couples
? Quels sont les couples ) (avec
(avec  et
et  dans
dans 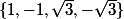 ) tels que
) tels que +b\sin(-\pi/4)=0) ?
?
Quel est exactement ton souci ? Qu'as-tu essayé ?
Pour la 1) : quel est le cosinus et le sinus de
Re: Dénombrement
Non, attention ! 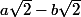 ne donne pas
ne donne pas 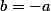
L'énoncé tel que tu !le donnes n'est pas super clair sur ce qu'est "le nombre de tirages".
J'interprète les choses de la manière suivante : il y a 20 boules dans l'urne. Il y a donc 20 possibilités pour la première boule et 19 pour la deuxième, ce qui fait 380 tirages possibles (le nombre d'arrangements de 2 boules parmi 20). Parmi ces 380 tirages possibles, combien y en a-t-il pour lesquels la propriété+b\sin(-\pi/4)= 0) est vérifiée ?
est vérifiée ?
L'énoncé tel que tu !le donnes n'est pas super clair sur ce qu'est "le nombre de tirages".
J'interprète les choses de la manière suivante : il y a 20 boules dans l'urne. Il y a donc 20 possibilités pour la première boule et 19 pour la deuxième, ce qui fait 380 tirages possibles (le nombre d'arrangements de 2 boules parmi 20). Parmi ces 380 tirages possibles, combien y en a-t-il pour lesquels la propriété
Re: Dénombrement
Alors, quels sont les couples ) qui vérifient la propriété ?
qui vérifient la propriété ?
Pour chacun de ces couples) , combien y a-t-il de tirages qui donnent ce couple (de tirages où la première boule porte de nombre
, combien y a-t-il de tirages qui donnent ce couple (de tirages où la première boule porte de nombre  et la deuxième boule le nombre
et la deuxième boule le nombre  ) ?
) ?
Pour chacun de ces couples
Re: Dénombrement
Pourquoi réponds-tu sans réfléchir ? Est-ce que 2 est un nombre porté par une boule ? N'y a-t-il pas d'autres cas possibles où les deux boules tirées portent le même nombre ?
Re: Dénombrement
Bien, et alors combien y a-t-il de tirages qui donnent le couple (1,1) (je rappelle qu'il y a dans l'urne 6 boules portant le n° 1) ?
Re: Dénombrement
Geometry Dash World said:
1) Déterminer le nombre de tirages que l on peut effectuer pour que -π/4 soit solution de (E).
Déterminer le nombre de tirages que l on peut effectuer pour que -π/4 soit solution de (E).
L'équation (E) est une équation trigonométrique. Pour que -π/4 soit solution de cette équation, il faut que le produit des nombres a et b soit égal à -3.
Il y a 6 boules numérotées 1, 4 boules numérotées √3, 5 boules numérotées -1 et 5 boules numérotées -√3.
Le nombre de tirages possibles est donc 6 * 10 = 60.
Parmi ces 60 tirages, il y a 6 tirages qui donnent un produit égal à -3 : (1, -√3), (1, -1), (√3, -1), (√3, -√3), (-1, 1), (-1, √3).
Donc, la réponse est 6.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
