Construire le tracé d'un circuit automobile : un problème de rotations !

[scull]

Bonjour à tous les passionnés de maths,

Je suis en train de créer un mini jeu de simulation automobile et je suis face à un problème d'ordre mathématique et plus précisément géométrique. Je souhaiterais construire la représentation d'un circuit automobile en partant d'un fichier qui est constitué de la manière suivante :

portions {
portion {
type
longueur
angle
rayon
sens
},
...
}

Chaque portion peut être de deux types différents : ligne droite ou virage. Dans le cas d'une ligne droite, seule la distance (en m) est renseignée. Dans le cas d'un virage, je renseigne son angle (en degrés), son rayon (en m), et son sens (gauche ou droite). Un circuit est donc constitué d'un ensemble de portions et me permet de calculer la vitesse et le comportement de mes voitures sur le circuit.

Le problème que je rencontre est pour construire une représentation graphique de mon circuit à partir de ce fichier. Pour cela, j'ai choisi le format SVG qui permet de construire des chemins, en position des points en se basant sur un repère unique. La stratégie que je pensais adopter est la suivante :
- partir du point (0,0)
- parcourir chaque portion
- pour une ligne droite positionner un point qui correspond au dernier point tracé + la longueur de la ligne droite, en prenant en compte l'angle courant
- pour un virage, positionner un point qui correspond au dernier point tracé + la longueur du virage + une rotation qui correspond à l'angle du virage
- mettre à jour l'angle courant en y ajoutant (ou en y soustraient, en fonction du sens du virage) l'angle du virage

J'ai trouvé plusieurs formules qui permettent de calculer les coordonnées d'un point en y appliquant une rotation, mais le problème vient du fait que cette rotation ne doit pas s'appliquer en fonction du repère du circuit, mais plutôt par rapport à la position du dernier point connue et de son angle. J'ai entendu parler de rotation qui prend en compte un changement de repère, mais mes recherches sont restées infructueuses.

Mon deuxième problème concerne les lignes droites et reprend le même thème : pour positionner le point qui correspond à la fin de ma ligne droite, je dois prendre en compte l'angle courant (donné par le dernier virage), il s'agit donc de continuer "en ligne droite", mais encore une fois, il ne s'agit pas simplement de faire une translation suivi d'une rotation en s'appuyant sur le repère du circuit, mais bien en faisant une rotation à partir du point précédent.

J'espère avoir décrit mon problème de façon la plus claire possible, n'hésitez pas à me demander des précisions que ce soit sur le fichier qui décrit le circuit, l'algorithmie où même mon besoin final.

Je remercie par avance tout ceux qui auront pris du temps pour lire cet article et éventuellement pour m'apporter votre connaissance sur le sujet.

Cordialement,
Scull

[fatal_error]

salut,

tu as qu'à considérer un vecteur directeur v (qui est la direction dans laquelle va ta voiture).
Trivialement pour une ligne droite, ton nouveau point est de la forme
p+a(t)*v, où a est un scalaire, p est ton dernier point.

Pour un virage, rebelotte tu considères ton vecteur v, je sais pas si ton angle c'est par rapport à v, ou par rapport au centre de ton virage, mais si on suppose par rapport à v...ben ton nouveau vecteur direction est donné par
v' = Mv, M la matrice de rotation d'angle ton angle

[scull]

salut,

tu as qu'à considérer un vecteur directeur v (qui est la direction dans laquelle va ta voiture).
Trivialement pour une ligne droite, ton nouveau point est de la forme
p+a(t)*v, où a est un scalaire, p est ton dernier point.

Pour un virage, rebelotte tu considères ton vecteur v, je sais pas si ton angle c'est par rapport à v, ou par rapport au centre de ton virage, mais si on suppose par rapport à v...ben ton nouveau vecteur direction est donné par
v' = Mv, M la matrice de rotation d'angle ton angle

Merci beaucoup pour ta réponse ! Malheureusement je suis un programmeur qui a un peu de mal avec les maths... Concrètement, que dois-je faire pour appliquer ta formule ?

Par exemple, je ne comprends pas comment exploiter cette notion de scalaire ou de matrice de rotation. Désolé, cela doit sembler triviale pour quelqu'un comme toi, mais c'est un peu obscur pour moi

[Ben314]

Salut,
Si, avant une portion donnée, le "bout" de ton circuit est en et l'angle "courant" et alors :

1) Une portion de ligne droite de longueur va se terminer en


2) Un virage à gauche () ou à droite () de rayon 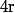aura son centre en



Donc la portion de virage en question va être paramétrée par



où la variable va partir de pour arriver à si l'angle de ton virage est (en augmentant pour les virages à gauche et en diminuant pour les virage à droite).

Le point d'arrivé du virage sera donc en :

[scull]

Salut,
Si, avant une portion donnée, le "bout" de ton circuit est en et l'angle "courant" et alors :

1) Une portion de ligne droite de longueur va se terminer en


2) Un virage à gauche () ou à droite () de rayon aura son centre en

Donc la portion de virage en question va être paramétrée par

où la variable va partir de pour arriver à si l'angle de ton virage est (en augmentant pour les virages à gauche et en diminuant pour les virage à droite).
Le point d'arrivé du virage sera donc en :

Super merci beaucoup, c'est très complet et très bien détaillé ! Je vais tenter d'implémenter ça et je vous tiens au courant Encore merci !

[fatal_error]

bien vu l'angle orienté (j'avais zappé)

Voilà un exemple dimplem non testé

Code: Tout sélectionner

function Circuit(){
  this.currentPoint = {x:0, y:0} //point courant
  this.v = {x:0, y:1}            //vecteur directeur
  this.positions = [
    {
      distance:22,
      radius:10,
      angle:0.22
      left:true
    },
    {
      distance:10
    },
    {
      distance:10,
      radius:3,
      left:false,
      angle:0.47
    }
  ]
}
Circuit.prototype.getNextPoint = function(){
  var position = this.positions.pop();
  if(this.isLine(position)){
    var x = distance * this.v.x;
    var y = distance * this.v.y;
    this.currentPoint = {x:x, y:y};
    return this.currentPoint;
  }else{
    //connaissant le radius, je présume que l'angle est l'angle au centre...
    //on prend le vecteur orthogonal à v
    //si à gauche, alors c'est v tourné de pi/2, si virage à droite, c'est v tourné de -pi/2
    var vAngle = Math.PI/2*(position.left?1:-1);
    var orthoV = rotate(vAngle, this.v);
    var rotationCenter = {
      x: this.currentPoint.x + position.radius*orthoV.x,
      y: this.currentPoint.y + position.radius*orthoV.y
    }

    //on rotate this.currentPoint d'angle position.angle de centre rotationCenter
    this.currentPoint = rotate(rotationCenter, position.angle*(position.left?1:-1), this.currentPoint);

    //on recalcule notre vecteur directeur, orthogonal au vecteur n = [rotationCenter, this.currentPoint]
    var n = {
      x: this.currentPoint.x - rotationCenter.x,
      y: this.currentPoint.y - rotationCenter.y
    }
    var nAngle = Math.PI/2*(position.left?1:-1);
    this.v = rotate(nAngle, n);
    //et on oublie pas de le normer
   var normV = Math.sqrt(Math.pow(this.v.x,2)+Math.pow(this.v.y,2))
   this.v.x /= Math.sqrt(normV);
   this.v.y /= Math.sqrt(normV);

    return this.currentPoint;
  }
}
Circuit.prototype.isLine = function(position){
  return !position.hasOwnProperty('radius');
}

function rotate(center, angle, point){
  if(arguments.length==2){
    //center has been omitted
    point = angle;
    angle = center;
    center = {
      x:0,
      y:0
    };
  }

  //on déplace le point comme si le centre était en 0
  var translatedPoint = {
    x:point.x - center.x,
    y:point.y - center.y
  };

  //on applique la matrice de rotation sur le point
  var a = Math.cos(angle);
  var b = Math.sin(angle);
  /* M = [
    [a, -b],
    [b, a]
  ] * translatedPoint*/
  var rotatedPoint = {
    x:a*translatedPoint.x - b*translatedPoint.y,
    y:b*translatedPoint.x - a*translatedPoint.y,
  }

  //on retranslate notre point à l'endroit ou il devrait etre
  return {
    x: rotatedPoint.x + center.x,
    y: rotatedPoint.y + center.y
  }

}


un peu différent que proposé par ben, jpensais pas que faudrait 30 min pour écrire 60 pauvres lignes :marteau:

[scull]

Bonjour à tous les deux !

Je poste pour vous dire un grand, grand merci pour votre aide, en m'inspirant de vos deux solutions j'ai pu écrire un algorithme qui répond parfaitement à mon besoin !

Un aperçu d'un circuit construit à partir du fichier source :
https://drive.google.com/file/d/0Bwogg2QmjTXWLThXZWxzU1AxdTg/view?usp=sharing

Et le circuit d'origine :
http://media.supercharged.fr/2011/02/monza.jpg

Je pense qu'on peut dire que c'est un succès !

Si j'arrive au bout de ce petit projet de jeu (à destination des mobiles), je vous en ferai parvenir un exemplaire

Bonne journée !