Congruence

[mathsinfo3456]

question :
determiner la forme de sentiers naturels n tel que 5 a la puissance n est congru a 1mode 13
est ce que c est bien n=8mod13?

[mathelot]

bonjour,
calcule modulo 13
détermine l'ordre de 5 , modulo 13,i.e, le plus petit entier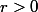 tel que

ensuite, si écris la division euclidienne de n par r.

on doit trouver l'équivalence

[mathsinfo3456]

merci

[mathsinfo3456]

pourriez vous me donner plus de details?

[Vassillia]

Bonjour,
Je milite pour le regroupement quand c'est exactement le même sujet, déjà posté là
https://www.maths-forum.com/cafe-mathematique/representations-des-entiers-t231423.html

[mathelot]

bonjour,
calcule modulo 13

je t'ai donné du travail, pourquoi ce n'est pas fait ?

[mathsinfo3456]

5,12,8,1

[mathelot]

5,12,8,1

donc





donc r=4. L'ordre de 5, modulo 13 est 4.

soit
on divise l'exposant n par 4 avec la division euclidienne.
Il existe m entier et entier naturel tel que




si alors mais donc
donc

réciproquement si alors il existe k entier naturel tel que n=4k
alors

[mathelot]

est ce que tu connaissais la division euclidienne d'un entier n par un entier q ?

[GaBuZoMeu]

Et voila comment mathelot fait l'exercice à la place de mathsinfo.

[mathelot]

Bon, j'ai un peu déplacé le centre d'intérêt, je souhaite que le fil s'oriente vers la division euclidienne, la notion indispensable pour les congruences.

@mathsinfo: qu'est ce que ça t'évoque, la division euclidienne dans ?

remarque: 13 étant un entier premier, et 5 étant premier avec 13, le petit théorème de Fermat donne

mais ici, l'ordre de 5 ,égal à 4, est plus petit que 12.

[mathsinfo3456]

ca fait plus de 15 ans que j ai vu ces notions je. m en rappelle pas bien

[mathelot]

Division euclidienne:
quand on divise 40 par 3, on cherche le plus grand multiple de 3 inférieur ou égal à 40.
Ici, ce plus grand multiple est 39. On calcule le reste de la division:
40-3 * 13=40-39=1
on écrit alors: 40=3*13+1
13 est le quotient et 1 est le reste. Le reste vérifie les inégalités

si l'on travaille avec des lettres, la division de l'entier n par l'entier p s'écrit:
il existe des entiers naturels q et r avec tels que:
n=pq+r

ensuite on définit une relation d'équivalence R entre entiers a et b modulo p:
a R b si et seulement si a-b est multiple de p.
on note
Cette relation signifie également que a et b ont le même reste dans la division par p.

https://fr.wikipedia.org/wiki/Division_euclidienne

[mathsinfo3456]

ben merci beaucoup c gentil d ta part