Bonjour, j'aimerais savoir s'il y a une manière et comment faire pour calculer le plus simplement/rapidement :
(P indice n-1)! Congrue à un nombre k modulo (P indice n)
Où P appartient à l'ensemble des nombres premiers,
n un naturel strictement plus grand que 2 et
k un naturel tel qui soit le plus petit possible.
Le problème est l'immensité du nombre (P indice n-1)! dù à sa factorielle lorsque P devient très grand. J'aimerais avoir une manière simple de réaliser la congruence sans avoir à calculer (P indice n-1) en entier.
Congruence et nombre premier
8 messages
- Page 1 sur 1
 Congruence et nombre premier
Congruence et nombre premier
Modifié en dernier par Baptiste789 le 22 Sep 2022, 19:04, modifié 1 fois.
Re: Congruence et nombre premier
J'ai fait une erreur, je vais modifier ça, je cherche congrue à un nombre n appartenant aux naturels le plus petit possible, modulo (P indice n).
Re: Congruence et nombre premier
On sait que si Q est un nombre premier autre que 2 , ! = -1 (mod Q))
Donc! = -1 (mod P_n ))
Plutôt que calculer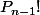 , tu peux calculer le produit des entiers entre
, tu peux calculer le produit des entiers entre 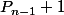 et
et 
Et ça revient en fait à calculer D! avec D=!)
Et évidemment, on n'a pas réellement besoin de faire le calcul de cette factorielle , dès que le produit dépasse , on simplifie.
, on simplifie.
Donc
Plutôt que calculer
Et ça revient en fait à calculer D! avec D=
Et évidemment, on n'a pas réellement besoin de faire le calcul de cette factorielle , dès que le produit dépasse
Re: Congruence et nombre premier
Je ne comprends pas votre raisonnement, pouvez-vous me faire des exemples s'il vous plaît ?
Re: Congruence et nombre premier
Regardons les nombres premiers 37 et 41.
On cherche le reste de la division de 37! par 41.
Mais 37!, c'est très grand.
On va s'intéresser à 40!
En fait, un résultat connu nous dit que le reste de la division de 40! par 41, c'est -1. (C'est 41-1 pour être plus rigoureux)
Donc 37! *38* 39* 40 =-1 modulo 41
Et je peux même remplacer 38, 39 et 40 par -3,-2 et -1 :
37! * (-3)! * (-2) * (-1)=-1
ça se simplifie :
37! * 3! = 1
Je calcule 3! , c'est facile, c'est 6.
Je cherche donc le nombre n (entre 0 et40) tel que n*6-1 soit un multiple de 41.
Ici, c'est facile, c'est 7
Le reste de la division de 37! par 41 est 7.
Sans calculatrice.
On cherche le reste de la division de 37! par 41.
Mais 37!, c'est très grand.
On va s'intéresser à 40!
En fait, un résultat connu nous dit que le reste de la division de 40! par 41, c'est -1. (C'est 41-1 pour être plus rigoureux)
Donc 37! *38* 39* 40 =-1 modulo 41
Et je peux même remplacer 38, 39 et 40 par -3,-2 et -1 :
37! * (-3)! * (-2) * (-1)=-1
ça se simplifie :
37! * 3! = 1
Je calcule 3! , c'est facile, c'est 6.
Je cherche donc le nombre n (entre 0 et40) tel que n*6-1 soit un multiple de 41.
Ici, c'est facile, c'est 7
Le reste de la division de 37! par 41 est 7.
Sans calculatrice.
Re: Congruence et nombre premier
J'ai tout compris merci de vos explications.
Cependant j'ai une dernière question, que ce passerait-il si on chercherait avec la factorielle première ?
C'est à dire avec l'exemple des deux nombres premiers 37 et 41, on chercherait la factorielle première de 37 (soit 37*31*29*23...) modulo 41. Il y a t-il une manière simple et plus ou moins rapide de pouvoir résoudre le problème sans calculatrice ou sommes-nous dans l'incapacité ?
Cependant j'ai une dernière question, que ce passerait-il si on chercherait avec la factorielle première ?
C'est à dire avec l'exemple des deux nombres premiers 37 et 41, on chercherait la factorielle première de 37 (soit 37*31*29*23...) modulo 41. Il y a t-il une manière simple et plus ou moins rapide de pouvoir résoudre le problème sans calculatrice ou sommes-nous dans l'incapacité ?
Re: Congruence et nombre premier
Je crois que le nom usité dans ce cas est 'primorielle' et non factorielle première.
Là, je ne vois aucune astuce.
Sauf évidemment à tout simplifier au fur et à mesure.
2*3*5*7*11*13*17*19*23*29*31*37
2*3*5*7=210=5*41+5=5
5*11=55=14
14*13=182=4*41+18
18*17=306=7*41+19
19*19=361=9*41-8
-8*23=-184=-4*41-20
-20*29=-580=-14*41-6
-6*31=-186=-5*41+19
19*37=703=410+293=410+7*41+6
Résultat=6 si je sais encore compter comme il faut.
Non garanti !
Là, je ne vois aucune astuce.
Sauf évidemment à tout simplifier au fur et à mesure.
2*3*5*7*11*13*17*19*23*29*31*37
2*3*5*7=210=5*41+5=5
5*11=55=14
14*13=182=4*41+18
18*17=306=7*41+19
19*19=361=9*41-8
-8*23=-184=-4*41-20
-20*29=-580=-14*41-6
-6*31=-186=-5*41+19
19*37=703=410+293=410+7*41+6
Résultat=6 si je sais encore compter comme il faut.
Non garanti !
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
