Comment définir une équation à partir d'une liste de points ?
16 messages
- Page 1 sur 1
Comment définir une équation à partir d'une liste de points ?
Bonjour
Voilà longtemps que j'ai oublié mes bases de Term C... (voire avant) :hum:
Je cherche à déterminer une équation, à partir d'une liste de points.
Les valeurs "empiriques" de base sont les suivantes:
1 50
10 34,30
20 28,40
30 25,60
40 23,58
50 21,86
60 20,30
70 18,83
80 17,41
90 16,03
100 14,68
110 13,57
120 12,65
130 11,87
140 11,20
150 10,62
160 10,11
170 9,66
180 9,27
... pour tendre vers 4 à l'infini
Bon, en tâtonnant, j'imagine quelque chose comme f(x)=a*log(x)/x+b, mais je suis sûr que quelqu'un va me dire, "mais non, le plus simple c'est...)
D'autre part existe-t-il un outil permettant de modifier avec la souris la position, la courbure etc... d'une courbe pour en obtenir l'équation à la volée ?
Merci pour vos éclairages.
jlefevre78
Voilà longtemps que j'ai oublié mes bases de Term C... (voire avant) :hum:
Je cherche à déterminer une équation, à partir d'une liste de points.
Les valeurs "empiriques" de base sont les suivantes:
1 50
10 34,30
20 28,40
30 25,60
40 23,58
50 21,86
60 20,30
70 18,83
80 17,41
90 16,03
100 14,68
110 13,57
120 12,65
130 11,87
140 11,20
150 10,62
160 10,11
170 9,66
180 9,27
... pour tendre vers 4 à l'infini
Bon, en tâtonnant, j'imagine quelque chose comme f(x)=a*log(x)/x+b, mais je suis sûr que quelqu'un va me dire, "mais non, le plus simple c'est...)
D'autre part existe-t-il un outil permettant de modifier avec la souris la position, la courbure etc... d'une courbe pour en obtenir l'équation à la volée ?
Merci pour vos éclairages.
jlefevre78
jlefevre78 a écrit:Bonjour
Voilà longtemps que j'ai oublié mes bases de Term C... (voire avant) :hum:
Je cherche à déterminer une équation, à partir d'une liste de points.
Les valeurs "empiriques" de base sont les suivantes:
1 50
10 34,30
20 28,40
30 25,60
40 23,58
50 21,86
60 20,30
70 18,83
80 17,41
90 16,03
100 14,68
110 13,57
120 12,65
130 11,87
140 11,20
150 10,62
160 10,11
170 9,66
180 9,27
... pour tendre vers 4 à l'infini
Bon, en tâtonnant, j'imagine quelque chose comme f(x)=a*log(x)/x+b, mais je suis sûr que quelqu'un va me dire, "mais non, le plus simple c'est...)
D'autre part existe-t-il un outil permettant de modifier avec la souris la position, la courbure etc... d'une courbe pour en obtenir l'équation à la volée ?
Merci pour vos éclairages.
jlefevre78
Bonjour
D'une façon générale, 2 points sont reliés par une droite équation y = ax + b
3 points sont reliés par une parabole équation y = ax² + bx + c
4 points sont reliés par une courbe en x3
5 points => courbe en x4
etc etc
500 points => une courbe en
Pour trouver chacun des 500 coefficients, il faut poser les 500 équations et remonter les coefficients petit à petit par la méthode des Pivots de Gauss.
Mais bon, pour ton ensemble de nombres allant à l'infini tout en tendant vers une limite, il vaut mieux se concentrer sur la limite elle-même...
Merci
Je dois repréciser ma question.
L'objectif est de d'utiliser l'équation pour une application pratique. Les points peuvent donc varier. L'idée est bien de trouver une "formule" qui permette de donner une liste de points plus régulière se rapprochant de la liste initiale.
Merci pour votre aide.
jlefevre78
Je dois repréciser ma question.
L'objectif est de d'utiliser l'équation pour une application pratique. Les points peuvent donc varier. L'idée est bien de trouver une "formule" qui permette de donner une liste de points plus régulière se rapprochant de la liste initiale.
Merci pour votre aide.
jlefevre78
jlefevre78 a écrit:Merci
Je dois repréciser ma question.
L'objectif est de d'utiliser l'équation pour une application pratique. Les points peuvent donc varier. L'idée est bien de trouver une "formule" qui permette de donner une liste de points plus régulière se rapprochant de la liste initiale.
Merci pour votre aide.
jlefevre78
Bonjour,
Cas classique de physique expérimentale! Tu peux utiliser une méthode de regression linéaire (la méthode des moindres carrés) ou toute autre méthode de regression (log, exponentielle, etc).
Ta calculatrice, si elle est un peu évoluée, te permettra sans doute de faire une régression linéaire, log ou exponentielle....
benekire2 a écrit:Sinon simple question: est-ce que ce sera toujours possible de déterminer l'équation d'une courbe, juste avec ses points ? Du genre si j'ai
A(1;2)
B(-4;2)
C(6;5)
D(3;-5)
E(8;-3)
F(12;-1)
Comment puis-je faire pour trouver l'équation de cette courbe? Merci!!
c'est l'objet même de la régresion linéaire (ou méthode des moindres carrés). Cette méthode te permet de calculer l'équation de la droite (les coeff a et b dans y=ax+b) qui passe le plus près possible de chacun des points d'une liste de points (xi,yi). N'importe quelle calculatrice stat possède cette fonction.
l'outil de base pour approximer une fonction par des polynômes a partir de points c'est l'approximation de Lagrange qui dit que:
pour tout x1,x2,...,xn n réels distincts et y1,y2,...yn n réels, il existe un unique polynôme de degré inférieur ou égal a n+1 tel que:
pour tout i de [|1,n|], P(xi)=P(yi)
il y a même une formule explicite, je vous laisse chercher sur google (flemme pour le latex lol)
Cependant cette technique ne fonctionne que pour un nombre fini de points.
Avec un nombre infini, le mieux est de prendre quelques uns et de vérifier si le polynôme trouvé approxime suffisamment bien le reste.
Ici, si tes y ont une limite ça va pas trop être possible... Je sais pas si il y a une technique miracle, en tout cas pour le faire à la main. Et si c'est vraiment du log(x)/x je doute qu'il y ait beaucoup de logiciels qui permettent de trouver des équations de ce type...
En espérant t'avoir aidé =)
pour tout x1,x2,...,xn n réels distincts et y1,y2,...yn n réels, il existe un unique polynôme de degré inférieur ou égal a n+1 tel que:
pour tout i de [|1,n|], P(xi)=P(yi)
il y a même une formule explicite, je vous laisse chercher sur google (flemme pour le latex lol)
Cependant cette technique ne fonctionne que pour un nombre fini de points.
Avec un nombre infini, le mieux est de prendre quelques uns et de vérifier si le polynôme trouvé approxime suffisamment bien le reste.
Ici, si tes y ont une limite ça va pas trop être possible... Je sais pas si il y a une technique miracle, en tout cas pour le faire à la main. Et si c'est vraiment du log(x)/x je doute qu'il y ait beaucoup de logiciels qui permettent de trouver des équations de ce type...
En espérant t'avoir aidé =)
Bonsoir,
Tu n'as pas défini de courbe mais seulement un ensemble de points, donc tu ne peux pas parler de « cette courbe » et encore moins trouver son équation. On peut chercher l'équation de courbes particulières qui passent par ces points ou pas trop loin en ajoutant des conditions supplémentaires (courbe représentative d'une fonction polynomiale de tel degré (avec le cas particulier de la droite)...).
benekire2 a écrit:Du genre si j'ai
A(1;2)
B(-4;2)
C(6;5)
D(3;-5)
E(8;-3)
F(12;-1)
Comment puis-je faire pour trouver l'équation de cette courbe?
Tu n'as pas défini de courbe mais seulement un ensemble de points, donc tu ne peux pas parler de « cette courbe » et encore moins trouver son équation. On peut chercher l'équation de courbes particulières qui passent par ces points ou pas trop loin en ajoutant des conditions supplémentaires (courbe représentative d'une fonction polynomiale de tel degré (avec le cas particulier de la droite)...).
Benekire,
si tu cherche une fonction qui passe par les points,(a_2,b_2),...,(a_n,b_n)) (avec évidement les
(avec évidement les  distincts), c'est assez simple :
distincts), c'est assez simple :
Prend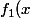={(x-a_2)(x-a_3)...(x-a_n)\over (a_1-a_2)(a_1-a_3)...(a_1-a_n)\ \) . Que vaut
. Que vaut ) ?
? ) ?
? ) ? ...
? ... ) ?
?
Peut tu me fabriquer sur le même modèle une fonction telle que
telle que =0,\ f_2(a_2)=1,\ f_2(a_3)=0,\ f_2(a_4)=0,\ ...,\ f_2(a_n)=0) ?
?
A t'on avis qu'est ce que j'aimerais que tu fabrique comme fonction ?
? 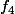 ? ...
? ...  ?
?
Que pense tu alors de la fonction=b_1\times f_1(x)+b_2\times f_2(x)+b_3\times f_3(x)+...+b_n\times f_n(x)) (quelle est sa valeur en
(quelle est sa valeur en 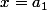 ? en
? en 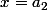 ? ... en
? ... en 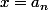 ? )
? )
Dernière question : que se passe t'il si à la fonction on ajoute
on ajoute (x-a_2)...(x-a_n)g(x)) où g est une fonction absoluement quelconque (quelle sont les nouvelles valeurs en
où g est une fonction absoluement quelconque (quelle sont les nouvelles valeurs en 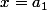 ? en
? en 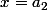 ? ... en
? ... en 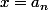 ? )
? )
Que déduit tu de tout cela ?
P.S. Si tu trouve "qu'il y a trop de lettres", tu est assez grand pour remplacer mes et
et  par les valeurs de ton exemple (avec n=6)
par les valeurs de ton exemple (avec n=6)
P.S.2 : Il faut aussi faire attention que TRES SOUVENT, ce que l'on cherche, ce n'est pas une fonction qui passe EXACTEMENT par les points mais une fonction LA PLUS SIMPLE POSSIBLE (par exemple affine) qui ne passe... pas trop loin des points (c'est le cas dans ce post...)
si tu cherche une fonction qui passe par les points
Prend
Peut tu me fabriquer sur le même modèle une fonction
A t'on avis qu'est ce que j'aimerais que tu fabrique comme fonction
Que pense tu alors de la fonction
Dernière question : que se passe t'il si à la fonction
Que déduit tu de tout cela ?
P.S. Si tu trouve "qu'il y a trop de lettres", tu est assez grand pour remplacer mes
P.S.2 : Il faut aussi faire attention que TRES SOUVENT, ce que l'on cherche, ce n'est pas une fonction qui passe EXACTEMENT par les points mais une fonction LA PLUS SIMPLE POSSIBLE (par exemple affine) qui ne passe... pas trop loin des points (c'est le cas dans ce post...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
