@mathelot, les équations différentielles apparaissent mais cela nécessiterait peut-être d'entrer plus dans les détails si tu le dis
J'ai essayé de me mettre à la logique dernièrement comme je n'y connaissais rien à part les tables de vérité et le calcul booléen. C'est intéressant mais je te rejoins azf sur le fait que c'est vraiment particulier comme domaine des mathématiques. A titre personnel, travailler dans ZFC me convient parfaitement, mais je veux bien regarder ce que cela donne avec moins d'axiomes par curiosité.
Le pire, si on remonte vraiment aux bases, c'est la logique intuitionniste. Au début, l'idée m'a parut bonne de faire des démonstrations constructives et après je me suis rendue compte du bazar que cela donne d'enlever le tiers exclus. J'ai essayé de comprendre le calcul des séquents pour m'y retrouver. En logique classique, pas trop de problème, il faut faire un peu attention pour introduire
et

mais j'y arrive.
Par contre, en logique intuitionniste, c'est une catastrophe, visiblement je ne me rends même pas compte quand j'utilise des trucs interdits, je n'arrive même pas à réaliser quels sont les séquents encore valables ou non.
Il parait qu'on a toujours
) \Leftrightarrow \forall x (\lnot P(x)))
par contre on a seulement
) \Rightarrow \lnot (\forall x P(x)))
. N'en déplaise à celui qui a eu l'idée, mon intuition ne voit pas du tout pourquoi.
Mais bon du coup, ce serait quoi les résultats les plus importants en logique, les théorèmes d'incomplétude de Godel peut-être ?
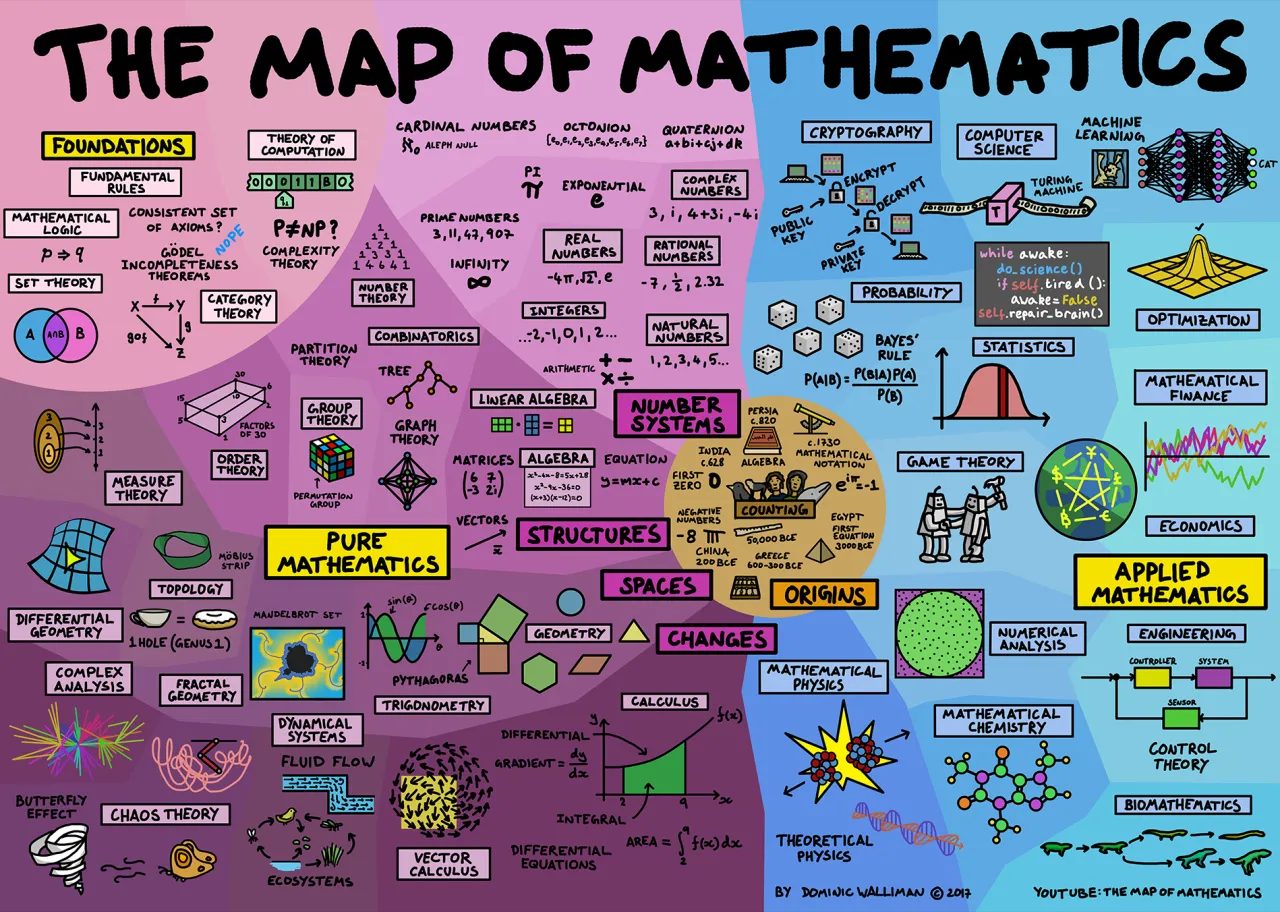 Je m'interroge :
Je m'interroge :