Bonjour
Je dois triangulariser la matrice d un endomorphisme pour étudier son rang, son image, son noyau en fonction d un paramètre m.
Dans les conseils qui sont donnés pour la résolution de l exercice, on commence par permuter deux colonnes (pour éviter de diviser par m) Puis ensuite on fait des transformations elementaires sur les lignes. Je croyais que soit on fait des transformations sur les colonnes, soit sur les lignes mais pas les deux mélangés?
Question : il est possible de faire une première permutation de colonnes, puis ensuite de faire les transformations sur les lignes?
Merci de me dire et de m expliquer.
Transformations de matrices
34 messages
- Page 1 sur 2 - 1, 2
par zygomatique » 31 Aoû 2015, 19:01
salut
permuter des colonnes consiste à permuter les images d'une base (et ceux de la base aussi)
ça ne change pas le rang ni l'image de l'endomorphisme
...
permuter des colonnes consiste à permuter les images d'une base (et ceux de la base aussi)
ça ne change pas le rang ni l'image de l'endomorphisme
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par PhilT » 31 Aoû 2015, 22:02
zygomatique a écrit:salut
permuter des colonnes consiste à permuter les images d'une base (et ceux de la base aussi)
ça ne change pas le rang ni l'image de l'endomorphisme
...
merci pour ces commentaires
par alphamethyste » 01 Sep 2015, 01:50
Salut
Comme il ne s'agit pas d'un papier/collé (à part deux chapitres le 4ième et 5ième que j'avais déjà écris) il se peut que même en vérifiant des erreurs que je n'ai pas vu se soient glissée dans ce post
bon alors : un peu tout ici ci-dessous
Sommaire
1. Opérations élémentaires sur une matrice
2. Espace propre
3. Diagonalisation d'une matrice diagonalisable
4. Trigonalisation d'une matrice trigonalisable
5. Espace hermitien normé
6. Algorithme du rang d'une matrice réelle ou complexe
1. Opérations élémentaires sur une matrice
Proposition I Opération élémentaire sur une matrice
On appelle opération élémentaire sur une matrice)
,
est une matrice de n lignes et de p colonnes sur un corps commutatif
donc commutatif par la loi . comme par exemple le corps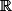
ou le corps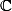 
bref ...on appelle opération élémentaire sur une matrice l'application A|-> UA ou A|-> AU
où U est une matrice de transposition, d'affinité ou de transvection
Toute opération élémentaire sur une matrice conserve son rang
ci-dessous description des matrices U de transposition, d'affinité ou de transvection
Proposition II Base canonique de)
on considère la matrice notée)
dont tous les coefficients sont nuls sauf celui en position (i,j) qui vaut 1
Soit de coefficients notés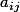 
alors on vérifie
dans cette proposition la famille)
avec 
et 
est dite base canonique de
et on note
la base canonique de )
l'ensemble des nxn matrice carrées
et enfin on note\subset \mathcal {M}_{n}(\mathbb {K}))
est l'ensemble des matrices carrées de taille n telles que celles-ci soient inversibles
cet ensemble constitue un groupe
Proposition III Produit matriciel et base canonique
Soient
alors on vérifie 
avec le symbole de Kronecker
qui vaut 1 pour i=j et sinon vaut 0
Matrice de transposition
Soient
avec 
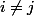
alors on appelle matrice de transposition toute matrice)
selon
)
on vérifie
avec se deduit de A en échangeant les lignes d'indices i et j
avec )
se deduit de B en échangeant les colonnes d'indices i et j
Matrice d'affinité
On appelle matrice d'affinité toute matrice définie par=I_n+(\lambda -1)E_{ii})
avec 
et 
C'est la matrice diagonale constituée de 1 sur la diagonale sauf à la ligne i où le coefficient est
Soient
et alors on vérifie
\in GL_n(\mathbb {K}))
=I_n)
^{-1}=D_i(\lambda ^{-1}))
D_i(\mu)=D_i(\lambda \mu))
A)
avec se deduit de A en multipliant la ligne d'indice i par 
)
avec se deduit de B en multipliant la colonne d'indice i par
Matrice de transvection
On appelle matrice de transvection toute matrice définie par=I_n+\lambda E_{ij})
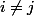pour avec et 
C'est la matrice dont tous les coefficient sont nuls sauf ceux de la diagonale qui valent 1et celui en position (i,j) qui vaut
Soient
et et 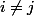alors on vérifie
\in GL_n(\mathbb {K}))
=I_n)
^{-1}=U_{ij} (-\lambda ))
U_{ij}(\mu)=U_{ij}(\lambda +\mu))
A)
avec se deduit de A en remplaçant la ligne d'indice i par elle même additionnée de la ligne d'indice j multipliée par
avec se deduit de B en remplaçant la colonne d'indice j par elle même additionnée de la colonne d'indice i multipliée par
Comme il ne s'agit pas d'un papier/collé (à part deux chapitres le 4ième et 5ième que j'avais déjà écris) il se peut que même en vérifiant des erreurs que je n'ai pas vu se soient glissée dans ce post
bon alors : un peu tout ici ci-dessous
Sommaire
1. Opérations élémentaires sur une matrice
2. Espace propre
3. Diagonalisation d'une matrice diagonalisable
4. Trigonalisation d'une matrice trigonalisable
5. Espace hermitien normé
6. Algorithme du rang d'une matrice réelle ou complexe
1. Opérations élémentaires sur une matrice
Proposition I Opération élémentaire sur une matrice
On appelle opération élémentaire sur une matrice
est une matrice de n lignes et de p colonnes sur un corps commutatif
donc commutatif par la loi . comme par exemple le corps
bref ...on appelle opération élémentaire sur une matrice l'application A|-> UA ou A|-> AU
où U est une matrice de transposition, d'affinité ou de transvection
Toute opération élémentaire sur une matrice conserve son rang
ci-dessous description des matrices U de transposition, d'affinité ou de transvection
Proposition II Base canonique de
on considère la matrice notée
dont tous les coefficients sont nuls sauf celui en position (i,j) qui vaut 1
Soit
alors on vérifie
dans cette proposition la famille
et on note
l'ensemble des nxn matrice carrées
et enfin on note
cet ensemble constitue un groupe
Proposition III Produit matriciel et base canonique
Soient
avec le symbole de Kronecker
Matrice de transposition
Soient
alors on appelle matrice de transposition toute matrice
on vérifie
Matrice d'affinité
On appelle matrice d'affinité toute matrice définie par
C'est la matrice diagonale constituée de 1 sur la diagonale sauf à la ligne i où le coefficient est
Soient
Matrice de transvection
On appelle matrice de transvection toute matrice définie par
C'est la matrice dont tous les coefficient sont nuls sauf ceux de la diagonale qui valent 1et celui en position (i,j) qui vaut
Soient
par alphamethyste » 01 Sep 2015, 01:57
2. Espace propre
deux définitions possibles:
l'une celle acceptée par tout le monde et que l'on utilisera ici
et l'autre de Monsieur Serge Lang du collectif Bourbaki dans son traité d'algèbre chapitre VII page 29 mais que l'on utilisera pas ici
dans sa définition il considère (mais c'est son choix) que pour toute valeur propre, le vecteur nul est aussi un vecteur propre associé à cette valeur propre
Attention : cette dernière définition ne sera pas utilisée ici
Definition acceptée par tout le monde et qui sera celle qu'on utilisera ici
Soit une valeur propre d'un endomorphisme 
de E un espace vectoriel de dimension n sur le corps commutatif
alors l'ensemble constitué des vecteurs propres de valeur propre et du vecteur nul 
forme un sous espace vectoriel de E que l'on note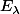 
appelé espace propre de associé à la valeur propre
on vérifie :=n-rang(\varphi-\lambda I_n))
Definition de Monsieur Serge Lang (mais que l'on utilisera pas ici)
Soient E un espace vectoriel sur un corps commutatif , un endomorphisme de E
on dit qu'un élément x de E est un vecteur propre de s'il existe 
tel que 
si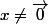
alors le scalaire 
est appelé valeur propre de correspondant à x
pour tout scalaire, le sous espace vectoriel formé des x tels que est appelé le sous espace propre de E relatif à
mais on ne choisira pas sa définition car dans celle-ci le vecteur nul est considéré comme étant un vecteur propre
3. Diagonalisation d'une matrice diagonalisable
je prend un exemple (et c'est le seul exemple qui servira ici donc bien regarder comment on s'y prend pour généraliser ça)
soit
d'un endomorphisme
on construit alors le polynôme P(X) caractéristique de cet endomorphisme en écrivant le déterminant de la matrice dont le déterminant est nul selon=\begin{pmatrix}m_{11}-\lambda &m_{12}\\m_{21}&m_{22}-\lambda \end{pmatrix}=0)
et où l'on véfifie donc=\det(M_{\lambda })=\lambda ^2-(m_{11}+m_{22})\lambda +\det(M)=0)
on note
les racines du polynôme donc ici dans l'exemple 
Ces racines constituent les valeurs propres de cet endomorphisme
et on dit que
est un vecteur propre associé à la valeur propre
si et seulement ci (définition acceptée par tout le monde) 
et 
par ailleurs on adopte une convention d'écriture ici dans l'exemple on note
alors on pose la matrice
cette matrice est la matrice du système d'équation
ainsi
alors
-Lorsque
on peut établir le vecteur propre
avec
et 
-Lorsque
on peut établir le vecteur propre
avec et 
-Lorsque
on peut établir le vecteur propre
avec
et 
-Lorsque
on peut établir le vecteur propre
avec et 
Alors si cette matrice M est diagonalisable on peut construire la matrice inversible
formée des deux vecteurs propres de M , 
et 
et vérifier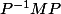
est une matrice diagonale
4. Trigonalisation d'une matrice trigonalisable
soit M une matrice d'un endomorphisme de E espace vectoriel de dimension n
on determine les vecteurs propres V1,V2 .... Va de cette matrice
puis on construit une base P=[V1,V2,...,Va,I1,I2...,Ib] de cet espace vectoriel avec les vecteurs propres de cette matrice et complétée par les vecteurs Ix formants la base canonique
alors si cette matrice est trigonalisable on verifie
est une matrice triangulaire supérieure
deux définitions possibles:
l'une celle acceptée par tout le monde et que l'on utilisera ici
et l'autre de Monsieur Serge Lang du collectif Bourbaki dans son traité d'algèbre chapitre VII page 29 mais que l'on utilisera pas ici
dans sa définition il considère (mais c'est son choix) que pour toute valeur propre, le vecteur nul est aussi un vecteur propre associé à cette valeur propre
Attention : cette dernière définition ne sera pas utilisée ici
Definition acceptée par tout le monde et qui sera celle qu'on utilisera ici
Soit
alors l'ensemble constitué des vecteurs propres de valeur propre
on vérifie :
Definition de Monsieur Serge Lang (mais que l'on utilisera pas ici)
Soient E un espace vectoriel sur un corps commutatif
on dit qu'un élément x de E est un vecteur propre de
si
pour tout scalaire
mais on ne choisira pas sa définition car dans celle-ci le vecteur nul est considéré comme étant un vecteur propre
3. Diagonalisation d'une matrice diagonalisable
je prend un exemple (et c'est le seul exemple qui servira ici donc bien regarder comment on s'y prend pour généraliser ça)
soit
on construit alors le polynôme P(X) caractéristique de cet endomorphisme en écrivant le déterminant de la matrice dont le déterminant est nul selon
et où l'on véfifie donc
on note
Ces racines
et on dit que
par ailleurs on adopte une convention d'écriture ici dans l'exemple on note
alors on pose la matrice
cette matrice est la matrice du système d'équation
alors
-Lorsque
avec
-Lorsque
avec
-Lorsque
avec
-Lorsque
avec
Alors si cette matrice M est diagonalisable on peut construire la matrice inversible
et vérifier
4. Trigonalisation d'une matrice trigonalisable
soit M une matrice d'un endomorphisme de E espace vectoriel de dimension n
on determine les vecteurs propres V1,V2 .... Va de cette matrice
puis on construit une base P=[V1,V2,...,Va,I1,I2...,Ib] de cet espace vectoriel avec les vecteurs propres de cette matrice et complétée par les vecteurs Ix formants la base canonique
alors si cette matrice est trigonalisable on verifie
par alphamethyste » 01 Sep 2015, 01:58
5.Espace hermitien normé
Un espace hermitien normé E est un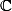-espace vectoriel E de dimension finie n
et muni d'un produit scalaire hermitien noté
et muni d'une norme hermitienne
Convention de notation
Dans ce qui suit on emploie les lettres v,w,x,y,z pour désigner tout vecteur de E
ces vecteurs que l'on représente par des matrices colonnes
par exemple avec la lettre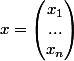
avec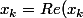+i.Im(x_k)\in \mathbb {C})
et 
on emploie les lettres I,J,K,L,M,N,P,Q pour désigner des matrices)
de p lignes et q colonnes
qui représentent des applications d'une espace vectoriel de dimension q vers un espace de dimension p
par exemple avec la lettre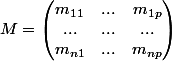
avec les composantes 
avec la notation pour la matrice identité
on emploie les lettres grecques
ou munies d'un indice ou pas pour désigner des scalaires
pour tout scalaire
on pose les notations suivantes :
désigne le module et 
le conjugué de ce nombre complexe
conditions
le produit scalaire et la norme hermitienne vérifient les deux assertions suivantes
première assertion : la forme de ce produit scalaire est sesquilinéaire à gauche
(donc linéaire à droite)
forme sesquilinéaire :
on dit que cette forme sesquilinéaire est à droite si et seulement si
et 
on vérifie
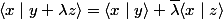est semi linéaire à droite
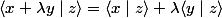est linéaire à gauche
et donc pour tout vecteur
, l'application 
de 
dans définie par
=\langle y\mid x\rangle)
est une forme linéaire
exemple de forme sesquilinéaire à droite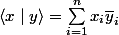
on dit que cette forme sesquilinéaire est à gauche si et seulement si
et on vérifie
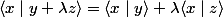est linéaire à droite
et donc pour tout vecteur, l'application de dans 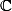définie par
=\langle x\mid y\rangle)
est une forme linéaire
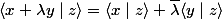est semi linéaire à gauche
exemple de forme sesquilinéaire à gauche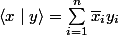
deuxième assertion :
a)
alors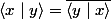 
b)si pour un
fixé et 
on vérifie toujours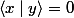 
alors obligatoirement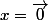 
c)si pour un fixé et on vérifie toujours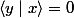 
alors obligatoirement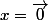
d)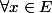
on vérifie 
e)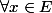
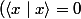on vérifie l'équivalence logique \Leftrightarrow (x=\overrightarrow {0}))
f)la norme hermitienne d'un vecteur est donnée par l'expression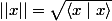 
et on vérifie l'inégalité de Cauchy-Schwarz
et l'inégalité triangulaire
pour la suite si on reste dans une géométrie définie par la forme sesquilinéaire à gauche suivante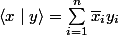
de sorte que
et on vérifie
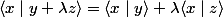est linéaire à droite
et donc pour tout vecteur, l'application de dans 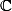définie par
est une forme linéaire
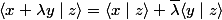est semi linéaire à gauche
démonstration
et on vérifie
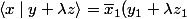+...+\overline {x}_n(y_n+\lambda z_n)= \overline {x}_1y_1+...+\overline {x}_ny_n+\lambda (\overline {x}_1z_1)+...+\lambda (\overline {x}_nz_n)=...)
est linéaire à droite
+i.Im(x_1)+((Re(\lambda)+i.Im(\lambda)).(Re(y_1)+i.Im(y_1)))}.z_1+...+\overline {Re(x_n)+i.Im(x_n)+((Re(\lambda)+i.Im(\lambda)).(Re(y_n)+i.Im(y_n)))}.z_n)
par conséquent
+i.Im(x_1) }+\overline {(Re(\lambda)+i.Im(\lambda)).(Re(y_1)+i.Im(y_1))} ).z_1+...+(\overline {Re(x_n)+i.Im(x_n) }+\overline {(Re(\lambda)+i.Im(\lambda)).(Re(y_n)+i.Im(y_n))} ).z_n=...)
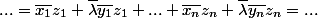
est semi linéaire à gauche
à partir de maintenant il s'agit de reconstruire tous les concepts que l'on peut
et qui sont reconnaissables en géométrie classique mais appliqués dans l'espace hermitien
défini par la forme sesquilinéaire à gauche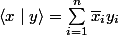
les deux premiers concepts : le vecteur nul et la colinéarité entre deux vecteurs
lorsque l'on peut definir un concept par l'utilisation de cette forme on ne doit pas s'en priver
puisque cette forme est une image abstraite de la representation naturelle de la géométrie classique
c'est la raison pour laquelle le formalisme de cet espace n'est pas representable mentalement tout comme
on peut mentalement se representer l'espace classique (en général à trois dimensions mais pas exclusivement)
la seule façon qu'il reste de ce representer la réalité de cet espace est de se cramponner à ce qu'il possede
comme points commun avec la réalitée de l'espace classique
et ce point commun en fait le plus important de tous est la forme choisie qui definis les concepts
dans un espace hermitien
c'est ainsi que dans ce qui suit on dira le point commun de tel concept tel qu'il est formulé ,
avec le cas classique de la géométrie euclidienne (où la forme considérée est une forme euclidienne)
Soit V un vecteur quelconque de cet espace alors ce vecteur est nul
et on note
si et seulement si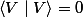 
(en géometrie euclidienne on retrouve la même définition qu'ici
mais cette fois ci avec l'utilisation de la forme euclidienne du produit scalaire)
Soient un couple de vecteurs
alors ce couple de vecteurs forme un systeme de vecteurs colinéaires
si et seulement si il existe un scalaire on note
tel que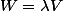 
il résulte de cela immédiatement une chose importante à dire
est que tout vecteur quelqu'il soit est toujours colinéaire au vecteur nul
cependant ici il ne faut pas oublier la sesquiniléarité et de plus à gauche
alors deux vecteurs sont colinéaires si et seulement si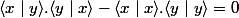
pour le vérifier il suffit de remplacer
par 
ou bien de remplacer 
par 
le concept d'orthogonalité
en considérant une forme sesquilinéaire à droite alors on pose le vecteur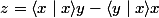
en considérant une forme sesquilinéaire à gauche alors on pose le vecteur
Lorsque x et y sont colinéaires alors on vérifie
et aussi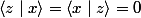 
Lorsque x et y ne sont pas colinéaires alors on vérifie
et aussi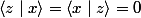
démonstration pour une forme sesquilinéaire à droite
la forme étant sesquilinéaire à droite alors on pose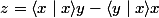
1a)admettons que x et y soient colinéaires alors dans ce cas il existe un scalaire tel que 
on verifie
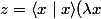- \langle \lambda x \mid x\rangle x= \lambda \langle x \mid x\rangle x-\lambda \langle x \mid x\rangle x=\overrightarrow {0})
1b)admettons que x et y soient colinéaires alors dans ce cas il existe un scalaire tel que 
on verifie
1c)admettons que x et y soient colinéaires alors dans ce cas et donc
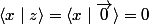et 
2a)admettons que x et y ne soient pas colinéaires
on vérifie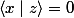
en effet
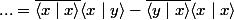
étant donné que
alors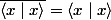 
de sorte que
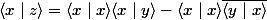
étant donné que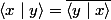
on obtiens donc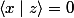 
2b)admettons que x et y ne soient pas colinéaires
on vérifie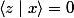
en effet
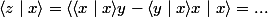
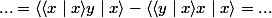
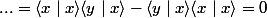
Un espace hermitien normé E est un
et muni d'un produit scalaire hermitien noté
Convention de notation
Dans ce qui suit on emploie les lettres v,w,x,y,z pour désigner tout vecteur de E
ces vecteurs que l'on représente par des matrices colonnes
par exemple avec la lettre
avec
on emploie les lettres I,J,K,L,M,N,P,Q pour désigner des matrices
de p lignes et q colonnes
qui représentent des applications d'une espace vectoriel de dimension q vers un espace de dimension p
par exemple avec la lettre
avec la notation pour la matrice identité
on emploie les lettres grecques
pour tout scalaire
conditions
le produit scalaire et la norme hermitienne vérifient les deux assertions suivantes
première assertion : la forme de ce produit scalaire est sesquilinéaire à gauche
(donc linéaire à droite)
forme sesquilinéaire :
on dit que cette forme sesquilinéaire est à droite si et seulement si
et donc pour tout vecteur
exemple de forme sesquilinéaire à droite
on dit que cette forme sesquilinéaire est à gauche si et seulement si
et donc pour tout vecteur
exemple de forme sesquilinéaire à gauche
deuxième assertion :
a)
b)si pour un
c)si pour un
d)
e)
f)la norme hermitienne d'un vecteur
et on vérifie l'inégalité de Cauchy-Schwarz
et l'inégalité triangulaire
pour la suite si on reste dans une géométrie définie par la forme sesquilinéaire à gauche suivante
de sorte que
et donc pour tout vecteur
démonstration
par conséquent
à partir de maintenant il s'agit de reconstruire tous les concepts que l'on peut
et qui sont reconnaissables en géométrie classique mais appliqués dans l'espace hermitien
défini par la forme sesquilinéaire à gauche
on rappelle donc que l'on vérifie
et donc pour tout vecteur
les deux premiers concepts : le vecteur nul et la colinéarité entre deux vecteurs
lorsque l'on peut definir un concept par l'utilisation de cette forme on ne doit pas s'en priver
puisque cette forme est une image abstraite de la representation naturelle de la géométrie classique
c'est la raison pour laquelle le formalisme de cet espace n'est pas representable mentalement tout comme
on peut mentalement se representer l'espace classique (en général à trois dimensions mais pas exclusivement)
la seule façon qu'il reste de ce representer la réalité de cet espace est de se cramponner à ce qu'il possede
comme points commun avec la réalitée de l'espace classique
et ce point commun en fait le plus important de tous est la forme choisie qui definis les concepts
dans un espace hermitien
c'est ainsi que dans ce qui suit on dira le point commun de tel concept tel qu'il est formulé ,
avec le cas classique de la géométrie euclidienne (où la forme considérée est une forme euclidienne)
Soit V un vecteur quelconque de cet espace
et on note
(en géometrie euclidienne on retrouve la même définition qu'ici
mais cette fois ci avec l'utilisation de la forme euclidienne du produit scalaire)
Soient un couple de vecteurs
si et seulement si il existe un scalaire on note
il résulte de cela immédiatement une chose importante à dire
est que tout vecteur quelqu'il soit est toujours colinéaire au vecteur nul
dans l'espace euclidien donc muni du produit scalaire euclidien -il s'agit d'une forme bilinéaire symétrique-
oùpeut prendre la forme
alors deux vecteurs sont colinéaires si et seulement si
cependant ici il ne faut pas oublier la sesquiniléarité et de plus à gauche
alors deux vecteurs sont colinéaires si et seulement si
pour le vérifier il suffit de remplacer
le concept d'orthogonalité
en considérant une forme sesquilinéaire à droite alors on pose le vecteur
en considérant une forme sesquilinéaire à gauche alors on pose le vecteur
Lorsque x et y sont colinéaires alors on vérifie
Lorsque x et y ne sont pas colinéaires alors on vérifie
démonstration pour une forme sesquilinéaire à droite
la forme étant sesquilinéaire à droite alors on pose
1a)admettons que x et y soient colinéaires alors dans ce cas il existe un scalaire
on verifie
1b)admettons que x et y soient colinéaires alors dans ce cas il existe un scalaire
on verifie
1c)admettons que x et y soient colinéaires alors dans ce cas
2a)admettons que x et y ne soient pas colinéaires
on vérifie
étant donné que
étant donné que
2b)admettons que x et y ne soient pas colinéaires
on vérifie
par alphamethyste » 01 Sep 2015, 01:59
6. Algorithme du rang d'une matrice réelle ou complexe
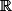Soit le corps ou le corps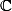
et soit une matrice non nulle)
dont on recherche son rang
on pose la convention de notation
attention de bien respecter cette convention de notation car l'algorithme Gram-Schmidt n'est valable uniquement que dans l'espace euclidien
pour le cas de matrices réelles on ramène toute matrice réelle à une matrice complexe en posant que toute les valeurs imaginaires de ses coefficients sont nuls
et qui désigne le produit du carré de la norme hermitienne du vecteur V par le projeté orthogonal de W sur l'hyperplan orthogonal de V
traitement préalable de la matrice
après donc avoir traité cette matrice là en éliminant les colonnes et lignes nulles
puis éliminés pour chaque série de vecteurs (colonnes ) colinéaires en en gardant un seul
puis de même sur la transposé de la matrice éliminés pour chaque série de vecteurs (colonnes ) colinéaires en en gardant un seul
le traitement au préalable de cette matrice donnant une matrice (pas forcément la même mais on garde la même notation pour cette matrice)
)
de composantes 
et dont on recherche le rang
si la matrice
ne possède qu'une seule colonne alors la matrice est de rang 1 mais sinon
on va construire deux suites finies de vecteurs notés
et 
par ailleurs à toute
ème colonne de la matrice dont on recherche le rang
on propose la notation\in K^n)
est donc un vecteur
cette construction s'effectuant dans un ordre précis en suivant les étapes
Etape N°1 :
on pose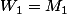
et 
et 
si
alors on élimine la deuxieme colonne de la matrice
cette élimination donne une nouvelle matrice M
si cette nouvelle matrice ne possede plus de deuxieme colonne alors la matrice est de rang 
mais sinon on reviens à l'étape 1
si
et que la matrice ne possède pas de troisième colonne alors la matrice est de rang 2 mais sinon on va à l'étape 2
Etape N°2 :
on pose
et 
et 
si alors on élimine la troisième colonne de la matrice
cette élimination donne une nouvelle matrice M
si cette nouvelle matrice ne possede plus de troisième colonne alors la matrice est de rang 
mais sinon on reviens à l'étape 2
si et que la matrice ne possède pas de quatrième colonne alors la matrice est de rang 3 mais sinon on va à l'étape 3
Etape N°3 :
on pose
si alors on élimine la troisième colonne de la matrice
cette élimination donne une nouvelle matrice M
si cette nouvelle matrice ne possede plus de quatrième colonne alors la matrice est de rang 
mais sinon on reviens à l'étape 3
si et que la matrice ne possède pas de cinquième colonne alors la matrice est de rang 4 mais sinon on va à l'étape 4
Etape N°4 :
on pose
et ainsi de suite ...
Soit
et soit une matrice non nulle
on pose la convention de notation
attention de bien respecter cette convention de notation car l'algorithme Gram-Schmidt n'est valable uniquement que dans l'espace euclidien
pour le cas de matrices réelles on ramène toute matrice réelle à une matrice complexe en posant que toute les valeurs imaginaires de ses coefficients sont nuls
et qui désigne le produit du carré de la norme hermitienne du vecteur V par le projeté orthogonal de W sur l'hyperplan orthogonal de V
traitement préalable de la matrice
après donc avoir traité cette matrice là en éliminant les colonnes et lignes nulles
puis éliminés pour chaque série de vecteurs (colonnes ) colinéaires en en gardant un seul
puis de même sur la transposé de la matrice éliminés pour chaque série de vecteurs (colonnes ) colinéaires en en gardant un seul
le traitement au préalable de cette matrice donnant une matrice (pas forcément la même mais on garde la même notation pour cette matrice)
si la matrice
on va construire deux suites finies de vecteurs notés
par ailleurs à toute
on propose la notation
cette construction s'effectuant dans un ordre précis en suivant les étapes
Etape N°1 :
on pose
si
cette élimination donne une nouvelle matrice M
si cette nouvelle matrice
si
Etape N°2 :
on pose
si
cette élimination donne une nouvelle matrice M
si cette nouvelle matrice
si
Etape N°3 :
on pose
si
cette élimination donne une nouvelle matrice M
si cette nouvelle matrice
si
Etape N°4 :
on pose
et ainsi de suite ...
par PhilT » 01 Sep 2015, 09:54
Donc, à partir d'une matrice donnée, on peut valablement obtenir une matrice triangulaire en effectuant des opérations élémentaires sur cette matrice sur ses lignes OU (inclusif) sur ses colonnes ?
C'est cela que pour l'instant je veux clarifier
Merci
C'est cela que pour l'instant je veux clarifier
Merci
par alphamethyste » 01 Sep 2015, 09:58
non
si elle est pas trigonalisable on ne peut pas
voir chap 4
si elle est pas trigonalisable on ne peut pas
voir chap 4
par PhilT » 01 Sep 2015, 10:20
D'accord, mais une chose n'est tjs pas claire pour moi par rapport à ce que je lis : dans la mesure où la matrice est trigonalisable, puisqu'on aboutit à une matrice triangulaire, est-ce qu'il est possible d'effectuer des opérations élémentaires sur les lignes ou (inclusif) sur les colonnes pour aboutir à cette matrice triangulaire ?
Merci de me dire
Merci de me dire
par Robot » 01 Sep 2015, 10:25
PhilT a écrit:Donc, à partir d'une matrice donnée, on peut valablement obtenir une matrice triangulaire en effectuant des opérations élémentaires sur cette matrice sur ses lignes OU (inclusif) sur ses colonnes ?i
Qu'entends-tu par "valablement" ? Tout est là.
On peut définir différentes relations d'équivalence entre matrices.
Dans une première relation d'équivalence, on peut dire que A est équivalente à B si on peut passer de A à B par des opérations élémentaires sur les lignes.
Dans une deuxième relation d'équivalence, on peut dire que A est équivalente à B si on peut passer de A à B par des opérations élémentaires sur les colonnes.
Enfin, dans une troisième relation d'équivalence, on peut dire que A est équivalente à B si on peut passer de A à B par des opérations élémentaires indifféremment sur les lignes ou sur les colonnes.
Toute la question est maintenant de savoir ce qui est préservé dans ces relations d'équivalence.
Pour la troisième, la seule chose préservée est le rang : deux matrices sont équivalentes au troisième sens si et seulement si elles ont même rang.
Le rang est aussi préservé pour les deux premières relations d'équivalence, qui sont plus restrictives. Mais on peut dire plus :
- Deux matrices sont équivalentes dans le premier sens si et seulement si elles ont même noyau.
- Deux matrices sont équivalentes dans le deuxième sens si et seulement si elles ont même image.
J'ajoute un conseil : ne pas tenir compte de ce que raconte alphamethyste.
par alphamethyste » 01 Sep 2015, 10:34
PhilT a écrit: Je dois triangulariser la matrice d un endomorphisme ...
j'avais compris que tu voulais faire ça
dans ce cas tu dois determiner les valeurs propres de ta matrice ... bref faire comme c'est dit chap3 et chap4 et voir si tu peux la triangulariser
maintenant si tu veux effectuer des operations elementaires sur une matrice voir chap 1
là tu peux le faire avec n'importe quelle matrice et comme j'ai dit le rang de la matrice transformée est conservée
par PhilT » 01 Sep 2015, 13:40
Robot a écrit:Qu'entends-tu par "valablement" ? Tout est là.
On peut définir différentes relations d'équivalence entre matrices.
Dans une première relation d'équivalence, on peut dire que A est équivalente à B si on peut passer de A à B par des opérations élémentaires sur les lignes.
Dans une deuxième relation d'équivalence, on peut dire que A est équivalente à B si on peut passer de A à B par des opérations élémentaires sur les colonnes.
Enfin, dans une troisième relation d'équivalence, on peut dire que A est équivalente à B si on peut passer de A à B par des opérations élémentaires indifféremment sur les lignes ou sur les colonnes.
Toute la question est maintenant de savoir ce qui est préservé dans ces relations d'équivalence.
Pour la troisième, la seule chose préservée est le rang : deux matrices sont équivalentes au troisième sens si et seulement si elles ont même rang.
Le rang est aussi préservé pour les deux premières relations d'équivalence, qui sont plus restrictives. Mais on peut dire plus :
- Deux matrices sont équivalentes dans le premier sens si et seulement si elles ont même noyau.
- Deux matrices sont équivalentes dans le deuxième sens si et seulement si elles ont même image.
J'ajoute un conseil : ne pas tenir compte de ce que raconte alphamethyste.
Tout d'abord merci de prendre du temps pour que je finisse par comprendre.
puisque vous prenez ce temps, je vais aussi en prendre pour vous indiquer le cas concret sur lequel je travaille ; tout sera alors plus clair pour tout le monde je pense.
Soit la matrice
On demande de discuter et trouver, suivant les valeurs de m, le rang, l'image et le noyau de l'endomorphisme f de
Pour aboutir à la matrice triangulaire inférieure
- permutation C1 avec C3 pour éviter de se retrouver avec des termes en m au dénominateur puis
- L2 <-- L2 + 2L3
- L1 <-- L1 + (m-1)L3
- L1 <-- L1 + L2
Ca me surprend car j'avais lu dans un cours consacré aux matrices - il est vrai au chapitre de l'application des opérations élémentaires au calcul de l'inverse d'une matrice - que "on peut travailler soit sur les lignes, soit sur les colonnes, mais il ne faut jamais faire les deux en même temps". Donc est-ce que cette règle - que je pensais valable pour tout calcul matriciel, ne concerne que la recherche de l'inverse d'une matrice par la méthode du pivot de Gauss ?
Pour revenir à notre cas, concernant rang, noyau et image de f, je pense pouvoir discuter selon la valeur de m, mais c'est la façon d'obtenir la matrice triangulaire qui permet cette discussion qui me pose question. C'est donc dans cette optique que je me pose la question et espère lever ce doute grâce à vos explications.
Merci par avance
par Robot » 01 Sep 2015, 14:07
Ce que tu dis de l'exemple n'éclaire en rien la question.
Bon, on fait un certain nombre d'opérations élémentaires sur les colonnes et sur les lignes de la matrice A (en prenant soin qu'on ne divise jamais par 0, quel que soit la valeur de m) et on se retrouve avec une matrice triangulaire A'.
Le point crucial, c'est : comment utilise-t-on ensuite cette matrice A', quelle information en tire-t-on sur la matrice A.
D'après ce que j'ai raconté dans mon message précédent, la seule information disponible immédiatement est : le rang de A est égal à celui de A'. Comme le rang de A' est assez facile à déterminer (il est toujours 3 sauf pour m = 0, -1, -3, cas que l'on peut étudier séparément), on connaît le rang de A en fonction des valeurs de m.
Mais pour la détermination du noyau et de l'image, il faudra retravailler : le noyau de A' n'est pas celui de A, l'image de A' n'est pas celle de A.
Tu évoques le calcul de l'inverse d'une matrice par opérations élémentaires. Ton cours a bien raison d'insister sur le fait que dans ce calcul, il ne faut absolument pas mélanger opérations élémentaires sur les lignes et opérations élémentaires sur les colonnes. Tout s'éclaire quand on connaît le lien entre
- opérations élémentaires sur les lignes et multiplication à gauche par une matrice inversible,
- opérations élémentaires sur les colonnes et multiplication à droite par une matrice inversible.
Connais-tu ce lien ?
Edit : j'ajoute qu'on pouvait sans peine procéder uniquement par opérations élémentaires sur les lignes dans l'exemple, en commençant par échanger L1 et L3 au lieu d'échanger C1 et C3. On se retrouve alors avec une matrice A'' triangulaire supérieure. Cette fois ci on a toujours que le rang de A'' est égal à celui de A, mais aussi que le noyau de A'' est égal à celui de A.
Bon, on fait un certain nombre d'opérations élémentaires sur les colonnes et sur les lignes de la matrice A (en prenant soin qu'on ne divise jamais par 0, quel que soit la valeur de m) et on se retrouve avec une matrice triangulaire A'.
Le point crucial, c'est : comment utilise-t-on ensuite cette matrice A', quelle information en tire-t-on sur la matrice A.
D'après ce que j'ai raconté dans mon message précédent, la seule information disponible immédiatement est : le rang de A est égal à celui de A'. Comme le rang de A' est assez facile à déterminer (il est toujours 3 sauf pour m = 0, -1, -3, cas que l'on peut étudier séparément), on connaît le rang de A en fonction des valeurs de m.
Mais pour la détermination du noyau et de l'image, il faudra retravailler : le noyau de A' n'est pas celui de A, l'image de A' n'est pas celle de A.
Tu évoques le calcul de l'inverse d'une matrice par opérations élémentaires. Ton cours a bien raison d'insister sur le fait que dans ce calcul, il ne faut absolument pas mélanger opérations élémentaires sur les lignes et opérations élémentaires sur les colonnes. Tout s'éclaire quand on connaît le lien entre
- opérations élémentaires sur les lignes et multiplication à gauche par une matrice inversible,
- opérations élémentaires sur les colonnes et multiplication à droite par une matrice inversible.
Connais-tu ce lien ?
Edit : j'ajoute qu'on pouvait sans peine procéder uniquement par opérations élémentaires sur les lignes dans l'exemple, en commençant par échanger L1 et L3 au lieu d'échanger C1 et C3. On se retrouve alors avec une matrice A'' triangulaire supérieure. Cette fois ci on a toujours que le rang de A'' est égal à celui de A, mais aussi que le noyau de A'' est égal à celui de A.
par alphamethyste » 01 Sep 2015, 15:01
merci pour la précision , en attendant je m'en tiens à mes maitres (désolé mais là travailler là sur ce que tu demande sans faire aucune recherche -écrire un determinant , determiner les valeurs propres et bosser tout seul) , je crains d'être obligé de te dire ça : mon ambition est d'être comme eux , mais ce que j'ai fait cette nuit ne me semble pas suffisant à te lire à présent
"Au chevet de Babylone- Les dieux inséparables abordent la terre, non comme une promise mais comme un bien privé. Ici-bas, ils ne peuvent être et chacun sans doute, qu'hommes et femmes, car ils savent tout des humains ... Cette pauvre et prétentieuse expérience les rendra vulnérables, un tantinet philosophes, quelque peu ordinaires, énormément violents et sanguinaires et si l'un d'eux s'exerce à l'humilité c'est qu'il est vaincu d'humanité. Tous néanmoins, auront bien des peines à retourner d'où ils viennent"
compagnie du kalïdoscope bleu
"Au chevet de Babylone- Les dieux inséparables abordent la terre, non comme une promise mais comme un bien privé. Ici-bas, ils ne peuvent être et chacun sans doute, qu'hommes et femmes, car ils savent tout des humains ... Cette pauvre et prétentieuse expérience les rendra vulnérables, un tantinet philosophes, quelque peu ordinaires, énormément violents et sanguinaires et si l'un d'eux s'exerce à l'humilité c'est qu'il est vaincu d'humanité. Tous néanmoins, auront bien des peines à retourner d'où ils viennent"
compagnie du kalïdoscope bleu
par alphamethyste » 01 Sep 2015, 15:56
.... être au chevet de Babylone ne signifie pas d'en profiter pour pioncer
par alphamethyste » 01 Sep 2015, 16:36
être au chevet de Babylone ne signifie pas d'en profiter pour pioncer (en plus eux c'est mes amis d'éternité-des frères de sang d'acier en fait )
"Au chevet de Babylone- Les dieux inséparables abordent la terre, non comme une promise mais comme un bien privé. Ici-bas, ils ne peuvent être et chacun sans doute, qu'hommes et femmes, car ils savent tout des humains ... Cette pauvre et prétentieuse expérience les rendra vulnérables, un tantinet philosophes, quelque peu ordinaires, énormément violents et sanguinaires et si l'un d'eux s'exerce à l'humilité c'est qu'il est vaincu d'humanité. Tous néanmoins, auront bien des peines à retourner d'où ils viennent"
compagnie du kalïdoscope bleu
"Au chevet de Babylone- Les dieux inséparables abordent la terre, non comme une promise mais comme un bien privé. Ici-bas, ils ne peuvent être et chacun sans doute, qu'hommes et femmes, car ils savent tout des humains ... Cette pauvre et prétentieuse expérience les rendra vulnérables, un tantinet philosophes, quelque peu ordinaires, énormément violents et sanguinaires et si l'un d'eux s'exerce à l'humilité c'est qu'il est vaincu d'humanité. Tous néanmoins, auront bien des peines à retourner d'où ils viennent"
compagnie du kalïdoscope bleu
34 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :