T.A.F (théorème des accroissements finis)
22 messages
- Page 1 sur 2 - 1, 2
T.A.F (théorème des accroissements finis)
Ex 1 :
Soit a,b ;) R tels que : 0 ;) a < b
a - Montrer que : 1/(1+b²) < (Arctan(b)- Arctan(a))/(b-a ) < 1/(1+a²)
b En déduire que : 1/(1+x²) < (Arctan(x))/x <1 ; ;)x >0
Ex 2 :
En appliquant le théorème des accroissements finis montrer que :
;)x <0 Arctan(x)< x/(1+x²)
Que quelquun m'explique :hein:
Soit a,b ;) R tels que : 0 ;) a < b
a - Montrer que : 1/(1+b²) < (Arctan(b)- Arctan(a))/(b-a ) < 1/(1+a²)
b En déduire que : 1/(1+x²) < (Arctan(x))/x <1 ; ;)x >0
Ex 2 :
En appliquant le théorème des accroissements finis montrer que :
;)x <0 Arctan(x)< x/(1+x²)
Que quelquun m'explique :hein:
Lamaths a écrit:Ah oui, c'est un peu fourbe quand on a pas l'habitude, on croit qu'il y a une variable alors que...
ça m'est aussi arrivé
Soit f(x) = Arctan(x)
D'après l'inégalité des accroissements finis, m (f(b)- f(a))/(b-a )M
où m et M sont respectivement le minimum et le maximum de f' sur [a,b]. Or f'(x)=1/(1+x²) est décroissante sur R+ donc atteint son maximum en a et son minimum en b.
On a donc M = 1/(1+a²) et m = 1/(1+b²) ce qui prouve le résultat.
c'est comme çà qu'il faut faire après intégration nespa ?
Ce que tu proposes est une autre démonstration de la question a- qui fonctionne très bien.
Ma version était plus pédestre.
Je vais tout écrire cette fois
À partir de :
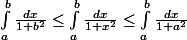
En intégrant (car 1/(1+b²) est une constante quand tu intègre par rapport à x, donc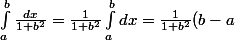) )
) ]_b^a \leq \frac{b-a}{1+a^2})
Et en divisant par b-a, qui est non nul, tu trouves bien :-Arctan(a)}{b-a} \leq \frac{1}{1+a^2})
Mais ce que tu proposes dans ton dernier message est une démonstration qui fonctionne parfaitement. (Sans que tu n'ai besoin de mes "intégrations" avant)
Ma version était plus pédestre.
Je vais tout écrire cette fois
À partir de :
En intégrant (car 1/(1+b²) est une constante quand tu intègre par rapport à x, donc
Et en divisant par b-a, qui est non nul, tu trouves bien :
Mais ce que tu proposes dans ton dernier message est une démonstration qui fonctionne parfaitement. (Sans que tu n'ai besoin de mes "intégrations" avant)
Lamaths a écrit:Ce que tu proposes est une autre démonstration de la question a- qui fonctionne très bien.
Ma version était plus pédestre.
Je vais tout écrire cette fois
À partir de :
En intégrant (car 1/(1+b²) est une constante quand tu intègre par rapport à x, donc)
Et en divisant par b-a, qui est non nul, tu trouves bien :
Mais ce que tu proposes dans ton dernier message est une démonstration qui fonctionne parfaitement. (Sans que tu n'ai besoin de mes "intégrations" avant)
Non, mais c'est à cause de tes explications que j'ai j'ai pu faire ma démonstration.
alors la conclusion au question b- suivant ma démonstration ?
Lamaths a écrit:Ta démonstration t'a permis de faire la question a-
Pour la b-, tu "changes" juste de notations en te plaçant dans un cas particulier de la question a-.
En plus clair : pose b=x et a=0 dans la 1ere question
Normalement le résultat tombe tout seul.
si je pose b=x et a=0 je vais trouver
1/(1+x²) 0 ??
C'est en gros ça.
Sur une copie j'écrirai :
D'après la question a- pour tous a,b ;) R tels que : 0 ;) a < b
1/(1+b²) < (Arctan(b)- Arctan(a))/(b-a ) < 1/(1+a²)
Posons a=0.
Donc pour tous b >0, on a : 1/(1+b²) < Arctan(b)/b <1
Ce qui est bien la question b-
Car ensuite que b s'appelle x, ou b... ça ne change rien, c'est une variable, sa seule contrainte c'est d'être strictement positive.
Sur une copie j'écrirai :
D'après la question a- pour tous a,b ;) R tels que : 0 ;) a < b
1/(1+b²) < (Arctan(b)- Arctan(a))/(b-a ) < 1/(1+a²)
Posons a=0.
Donc pour tous b >0, on a : 1/(1+b²) < Arctan(b)/b <1
Ce qui est bien la question b-
Car ensuite que b s'appelle x, ou b... ça ne change rien, c'est une variable, sa seule contrainte c'est d'être strictement positive.
Lamaths a écrit:C'est en gros ça.
Sur une copie j'écrirai :
D'après la question a- pour tous a,bR tels que : 0
a 0, on a : 1/(1+b²) < (Arctan(b) <1
Ce qui est bien la question b-
Car ensuite que b s'appelle x, ou b... ça ne change rien, c'est une variable, sa seule contrainte c'est d'être strictement positive.
aaah Ouii x) j'ai fais comme le correcteur sais ce qui tourne dans ma tete x)
j'ai cru que j'ai résolu l'ex 2 alors que j'ai fais juste la démonstration de la question a- x)
Soit x<0.
D'après le théorème des accroissement finis il existe c dans ]x,0[ tel que
Arctan(x)-arctan(0)= (x-0)*(Arctan)'(c)
Arctan(0)=0 et (arctan)'=1/(1+x²)
Donc Arctan(x)=x/(1+c²)
Si xc², donc 1/(1+x²)<1/(1+c²)
Or comme x est négatif, multiplier par x change le signe des inégalités, donc x/(1+x²)>x/(1+c²)
D'où, en utilisant la dernière inégalité : Arctant(x) (= x/(1+c²) ) < x/(1+x²)
D'après le théorème des accroissement finis il existe c dans ]x,0[ tel que
Arctan(x)-arctan(0)= (x-0)*(Arctan)'(c)
Arctan(0)=0 et (arctan)'=1/(1+x²)
Donc Arctan(x)=x/(1+c²)
Si x
Or comme x est négatif, multiplier par x change le signe des inégalités, donc x/(1+x²)>x/(1+c²)
D'où, en utilisant la dernière inégalité : Arctant(x) (= x/(1+c²) ) < x/(1+x²)
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
