Suite récurrente coriace
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Graigi
- Messages: 6
- Enregistré le: 13 Juil 2016, 08:28
-
 par Graigi » 13 Juil 2016, 08:36
par Graigi » 13 Juil 2016, 08:36
Bonjour à tous,
Je fais en ce moment face à une suite récurrente assez coriace dont je connais l'expression de u(n+1) en fonction de u(n) :
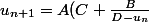)
Je souhaite connaitre l'expression de u(n) pour tout n, le premier terme étant u(2) que je connais.
Pourriez-vous m'éclairer ?
Merci !
-
Robot
 par Robot » 13 Juil 2016, 08:53
par Robot » 13 Juil 2016, 08:53
La fonction
)
est une homographie. La méthode classique pour étudier les suites homographiques est de rechercher les points fixes de l'homographie. S'il y a deux points fixes

et

, la suite
_n)
est une suite géométrique.
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 13 Juil 2016, 08:54
par Razes » 13 Juil 2016, 08:54
C'est quoi les valeurs de
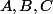
et
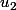
?
Il faut passer par le biais d'une transformation de suite du type:

Trouver les valeurs adéquates de
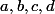
pour lesquelles

est une suite géométrique (sous certaine conditions).
Déterminer

en fonction de

Déterminer

en fonction de

en utilisant les résultats trouvés
-
Graigi
- Messages: 6
- Enregistré le: 13 Juil 2016, 08:28
-
 par Graigi » 13 Juil 2016, 09:57
par Graigi » 13 Juil 2016, 09:57
Merci pour vos réponses rapides.
Je suis donc passé par la méthode de la fonction homographique et ai déterminé ses points fixes a et b qui sont :
\pm \sqrt{(AC+D)^{2}-4A(CD+B)}}{2})
(A, B, C et D sont de constantes dont l'expression est plutôt longue que je n'écrirai pas ici.)
Il faut donc maintenant que je détermine les valeurs c et d telles que

soit géometrique, à savoir

Je ne comprend pas bien la démarche de cette méthode, à quoi cela nous sert-il et comment faire ?
Modifié en dernier par
Graigi le 13 Juil 2016, 10:17, modifié 1 fois.
-
Robot
 par Robot » 13 Juil 2016, 10:02
par Robot » 13 Juil 2016, 10:02
Tu as une définition curieuse de suite géométrique !
La suite
_n)
est dite géométrique quand il existe une constante

telle que, pour tout entier naturel

,

.
S'il s'agit d'un exercice, tu devrais remplacer A, B C et D par leurs valeurs : ça se simplifie sûrement !
-
Graigi
- Messages: 6
- Enregistré le: 13 Juil 2016, 08:28
-
 par Graigi » 13 Juil 2016, 10:23
par Graigi » 13 Juil 2016, 10:23
Oui autant pour moi j'ai écris trop vite, je modifie mon message précédent.
Il ne s'agit malheureusement pas d'un exercice, l'expression de u est la forme la plus simple possible (je travaille sur un projet perso).
Pour finir la résolution, faut-il que je remplace

par son expression en fonction de

dans l'expression de

? Je ne vois pas à quoi cela va nous mener !
-
Robot
 par Robot » 13 Juil 2016, 10:39
par Robot » 13 Juil 2016, 10:39
L'expression du terme général d'une suite géométrique n'est pas trop dure à trouver. Si tu as l'expression de

comme fonction de

, celle de

ne devrait pas non plus être trop dure à trouver. C'est tout.
-
Graigi
- Messages: 6
- Enregistré le: 13 Juil 2016, 08:28
-
 par Graigi » 13 Juil 2016, 13:51
par Graigi » 13 Juil 2016, 13:51
Je suis passé par une autre méthode similaire mais je ne suis pas sûr du résultat :
- J'ai mis

sous forme "homographique" :

en posant g = -AC, h = AB + ACD, c = -1 et d=D :

- Je cherche

et

tels que

Ils sont donnés par les racines de l'équation cr² + (d-g)r-h = 0
donc
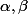
=
^{2}+4hc}}{2c})
-

est géométrique de raison

donc

(puisque je connais
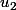
)
- Je peux en déduire

pour tout n

2 :
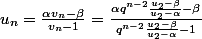
Qu'en pensez-vous ?
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 13 Juil 2016, 15:45
par Razes » 13 Juil 2016, 15:45
=\frac{u_n+3}{2u_n})
Point fixe
=x)
: les solutions sont

et
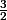
}{u_n-\frac{3}{2}}=\frac{u_n+1}{u_n-\frac{3}{2}})
+1}{(\frac{u_n+3}{2u_n})-\frac{3}{2}}=\frac{3u_n+3}{-2u_n+3}=\frac{3}{2}\frac{u_n+1}{u_n-\frac{3}{2}}=\frac{3}{2}v_n)
Donc

suite géométrique de raison

On obtient :
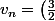^nv_0)
A partir de

on cherche

en fonction de

qu'on remplace par son expression. (De même

en fonction de

et vice versa)
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 13 Juil 2016, 15:48
par Razes » 13 Juil 2016, 15:48
-
Robot
 par Robot » 13 Juil 2016, 16:34
par Robot » 13 Juil 2016, 16:34
Graigi a écrit:Je suis passé par une autre méthode similaire
....
Qu'en pensez-vous ?
C'est très exactement la méthode que je t'indiquais.

-
Graigi
- Messages: 6
- Enregistré le: 13 Juil 2016, 08:28
-
 par Graigi » 13 Juil 2016, 22:22
par Graigi » 13 Juil 2016, 22:22
Merci Razes pour cet exemple, n'est-ce pas la méthode que j'ai employée ?
-
Robot
 par Robot » 13 Juil 2016, 22:39
par Robot » 13 Juil 2016, 22:39
C'est la méthode que tout le monde emploie pour traiter les suites homographiques. Il y a un cas spécial quand l'homographie a un point fixe double.
-
Graigi
- Messages: 6
- Enregistré le: 13 Juil 2016, 08:28
-
 par Graigi » 14 Juil 2016, 08:44
par Graigi » 14 Juil 2016, 08:44
Si ma suite ne converge pas est-ce que cette méthode est toujours valable ?
-
Robot
 par Robot » 14 Juil 2016, 10:07
par Robot » 14 Juil 2016, 10:07
La convergence n'a rien à voir dans l'expression des termes d'une suite homographique. Et on a toujours convergence vers le point fixe attractif, sauf si la raison q de la suite géométrique est de module 1.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 14 Juil 2016, 12:47
par zygomatique » 14 Juil 2016, 12:47
salut
Robot a écrit:C'est la méthode que tout le monde emploie pour traiter les suites homographiques. Il y a un cas spécial quand l'homographie a un point fixe double.
et c'est quoi le truc quand on a un point fixe double ?
quel changement de variable faut-il faire ? (ou autre chose)
merci par avance

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 14 Juil 2016, 13:13
par Razes » 14 Juil 2016, 13:13
Soit

le point fixe.

; Avec

à déterminer. qui prend la forme d'une suite arithmétique avec

-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 14 Juil 2016, 13:14
par Kolis » 14 Juil 2016, 13:14
Bonjour !
Si
=\dfrac{at+b}{ct+d})
et
=t)
admet la racine double

on a aussi

et
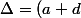^2-4(ad-ba)=0)
.
Alors,
-\alpha}=\mu+\dfrac1{t-\alpha},\; \mu)
constante, à calculer par utilisation d'une valeur particulière.
Ainsi la suite

est une suite arithmétique, ce qui permet de calculer explicitement

.
-
Robot
 par Robot » 14 Juil 2016, 13:40
par Robot » 14 Juil 2016, 13:40
Un petit coup de droite projective complexe rend tout lumineux. On envoie un point fixe

à l'infini et l'autre point fixe

en zéro en conjuguant par l'homographie

. On se retrouve avec une transformation affine qui a 0 comme point fixe, donc une homothétie
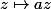
. S'il y a un seul point fixe double

, on l'envoie à l'infini en conjuguant par l'homographie

. On se retrouve avec une transformation affine sans point fixe, donc une translation

.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 14 Juil 2016, 14:44
par zygomatique » 14 Juil 2016, 14:44
merci pour ces info ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités

