Norme Euclidienne Matrice
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ineedi2
- Membre Naturel
- Messages: 60
- Enregistré le: 09 Jan 2008, 18:31
-
 par Ineedi2 » 22 Oct 2012, 12:57
par Ineedi2 » 22 Oct 2012, 12:57
Bonjour,
Voilà je dois calculer r le conditionnement de A ( une matrice ) relativement à la norme euclidienne.
Je crois savoir qu'il se calcule de cette façon: r = || A^(-1) || * || A || .
Le problème est que j'ignore que est la norme euclidienne pour une matrice ....
Je vous remercie d'avance !
-
Ineedi2
- Membre Naturel
- Messages: 60
- Enregistré le: 09 Jan 2008, 18:31
-
 par Ineedi2 » 22 Oct 2012, 13:00
par Ineedi2 » 22 Oct 2012, 13:00
Je viens de lire ça:
La norme de A est donc la plus grande des valeurs singulières de A (les valeurs singulières de A sont, par définition, les racines carrées des valeurs propres de t(A)*A.
t(A) = transposée de A
Vous justifiez?

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 03:29
-
 par raito123 » 22 Oct 2012, 13:11
par raito123 » 22 Oct 2012, 13:11
La norme euclidienne pour une matrice est A est
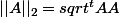
.
Tu peux démontrer qu'elle découle d'un produit scalaire.
Les multiples ne doivent pas être utilisés sans nécessité
-
Ineedi2
- Membre Naturel
- Messages: 60
- Enregistré le: 09 Jan 2008, 18:31
-
 par Ineedi2 » 22 Oct 2012, 13:14
par Ineedi2 » 22 Oct 2012, 13:14
raito123 a écrit:La norme euclidienne pour une matrice est A est
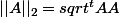
.
Tu peux démontrer qu'elle découle d'un produit scalaire.
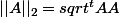
n'est pourtant pas un réel ?

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 03:29
-
 par raito123 » 22 Oct 2012, 13:28
par raito123 » 22 Oct 2012, 13:28
Oui oui autant pour moi. Voilà la bonne norme :
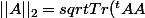})
Les multiples ne doivent pas être utilisés sans nécessité
-
Ineedi2
- Membre Naturel
- Messages: 60
- Enregistré le: 09 Jan 2008, 18:31
-
 par Ineedi2 » 22 Oct 2012, 13:40
par Ineedi2 » 22 Oct 2012, 13:40
raito123 a écrit:Oui oui autant pour moi. Voilà la bonne norme :
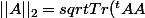})
Merci c'est gentil, bonne journée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
