Lois de groupe continues sur R

[ffpower]

Salut! Je viens de prendre la résolution d'essayer de poster des exos un peu plus souvent, histoire qu'il n'y ait pas de l'action que dans le forum lycée :)

Donc voila :
Soit * une loi de groupe sur R, telle que pour tout x, les applications y->x*y et y->y*x sont continues. Montrer que (R,*) est isomorphe à (R,+). ( ce qui implique en particulier que * est nécessairement commutative )

Bonne chance!

[Nightmare]

Yo,

vers quels outils s'orienter? Un indice ne serait pas de trop...

:happy3:

[Finrod]

Avec la multiplication, ça m'a l'air continu pour tout x. Mais (R,) n'est pas iso à (R,+) vu qu'il contient un élt absorbant 0.

[Doraki]

Au hasard je vois 2 étapes :

- pour x différent de e, la suite e, x, x*x, x*x*x,... est strictement monotone et tend vers +/- l'infini.

- l'application x -> x*x (ou carrément (x,y) -> x*y) est continue.
(comme ça on bouche les trous)

[Ben314]

Avec la multiplication, ça m'a l'air continu pour tout x. Mais (R,) n'est pas iso à (R,+) vu qu'il contient un élt absorbant 0.

Le léger problème, c'est que (R,) n'est pas un groupe...

[Finrod]

Le léger problème, c'est que (R,) n'est pas un groupe...

C'est tout moi ça.

et avec , ça devrait donc être iso à (R,+).

[ffpower]

Ben en fait dans mon énoncé, c'est une loi sur R tout entier, pas sur R*. Par contre on peut remplacer R par un intervalle. Donc ca marche pour R+* muni de la multiplication ( je vous laisse trouver l'isomorphisme^^)

Pour répondre à Night, la solution ( enfin ma solution ) n'utilise aucune théorie avancée, que de l'analyse réelle de bas étage. Et la piste principale, c'est :
( arriver à définir un analogue de "x puissance a" pour x,a dans R )

[Ben314]

En essayant de suivre les étapes suggérées par Doraki qui permettraient de construire "pas à pas" un isomorphisme de (R,+) sur (R,*) :
- L'application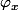 :y->x*y est continue, bijective () et, lorsque x est distinct du neutre e de *, sans point fixe (x*y=y x=e).
Elle est donc strictement croissante (y compris pour x=e où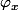 =Id)
- Si on part d'un fixé tel que e, en appliquant en cascade 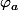on a e
La suite tend forcément vers +oo car sinon elle tendrait vers un point fixe de 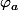qui n'a pas de point fixe.
De même, en appliquant en cascade on a avec

Tout cela permet déjà de poser pour tout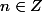

Reste la deuxième partie du "programme Doraki" consistant à montrer (au moins) que (R,*) est 2-divisible, c'est à dire que pour tout x il existe un y tel que y*y=x ce qui, comme Doraki le dit permettra de "boucher les trous" car on pourra définir , , ...
et la monotonie de permettra de compléter à R tout entier.

Edit : je n'avais pas vu "l'indic" de ffpower qui de toute façon dit la même chose que la suggestion de Doraki (et qui, à mon avis est la seule "voie" possible)

[ffpower]

Trés bon début, c'était bien la peine que je mette mon indic finalement^^

[Ben314]

Bon, déjà, le fait que pour x fixé les applications y->x*y et y->y*x sont strictement croissantes (pour la deuxième fonction, on utilise texto le même argument que pour la première) implique que, si x>x' on a x*x>x*x'>x'*x' donc x->x*x=x² est strictement croissante.
Ensuite, le fait que tend vers l'infini (a>e fixé) suffit à prouver que x² tend vers +oo lorsque x->+oo (de même x²->-oo lorsque x->-oo).

Il ne reste plus qu'à montrer ce qui me semble être le "point délicat", c'est à dire la continuité de x->x² pour pouvoir conclure.

[ffpower]

Edit : je n'avais pas vu "l'indic" de ffpower qui de toute façon dit la même chose que la suggestion de Doraki (et qui, à mon avis est la seule "voie" possible)

C'est ce que je pensais, mais l'objectif en vue ne semblait pas clairement précisé dans le post de Doraki. On va dire que j'ai clarifié ce point de vue pour les autres..
Sinon, au sujet de l'unique voie possible, je sais juste qu'il existe une solution directe dans le cas où la loi est C^1, en posant theta comme étant solution de je sais plus quelle équa diff. Mais bon au final c'est moins général et moins naturel comme méthode..

[ffpower]

Bon, déjà, le fait que pour x fixé les applications y->x*y et y->y*x sont strictement croissantes (pour la deuxième fonction, on utilise texto le même argument que pour la première) implique que, si x>x' on a x*x>x*x'>x'*x' donc x->x*x=x² est strictement croissante.
Ensuite, le fait que tend vers l'infini (a>e fixé) suffit à prouver que x² tend vers +oo lorsque x->+oo (de même x²->-oo lorsque x->-oo).

Il ne reste plus qu'à montrer ce qui me semble être le "point délicat", c'est à dire la continuité de x->x² pour pouvoir conclure.

Toujours tout bon..Je dirais juste que c'est plus simple de dire que si x>e, x²>x, pour justifier la limite en l'infini..

[Doraki]

Pour la continuité de (x,y) -> x*y, il me semble que ça marche en utilisant le fait que les fonctions x -> x*y et x -> y*x sont croissantes et continues.
J'devrais vérifier...

[Finrod]

- L'application :y->x*y est continue, bijective () et, lorsque x est distinct du neutre e de *, sans point fixe (x*y=y x=e).
Elle est donc strictement croissante.

Pourquoi nécessairement croissante et pas seulement monotone ?

[Doraki]

Elle est sans point fixe donc elle peut pas être décroissante.

[Finrod]

Elle est sans point fixe donc elle peut pas être décroissante.

Ah ok, oui. Sinon elle couperait la première bissectrice.

[skilveg]

et avec , ça devrait donc être iso à (R,+).

Plutôt à vu que est d'ordre deux.