Arccos
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
exilim
- Membre Naturel
- Messages: 95
- Enregistré le: 23 Sep 2006, 17:05
-
 par exilim » 24 Nov 2006, 19:11
par exilim » 24 Nov 2006, 19:11
Bonsoir !
est-il possible de simplifier Arccos (
}{2})
) parce que personnellement je sèche...
merci
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Nov 2006, 19:27
par tize » 24 Nov 2006, 19:27
Bonsoir,
rappel:
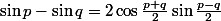
avec
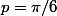
et
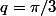
, on a :
=1/2)
et
=sqrt{3}/2)
d'ou
}{2} = sin(\pi/6)-sin(\pi/3) = 2cos(\pi/4)sin(-\pi/6) = -cos(\pi/4)=cos(\pi-\pi/4)=cos(3\pi/4))
et finalement :
}{2}) = Arcos(cos(3\pi/4))=3\pi/4)
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 24 Nov 2006, 19:28
par Quidam » 24 Nov 2006, 19:28
exilim a écrit:Bonsoir !
est-il possible de simplifier Arccos (
}{2})
) parce que personnellement je sèche...
merci
Moi aussi : si Arccos (
}{2})
) =

, alors p et q sont de grands entiers ... Si ce n'est pas le cas, alors, je n'ai aucune idée.
Es-tu sûr de ta formule ? Parce que si elle est légèrement différente, alors je pourrais peut-être avoir une idée...
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Nov 2006, 21:08
par tize » 24 Nov 2006, 21:08
tize a écrit:Bonsoir,
rappel:
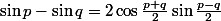
avec
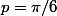
et
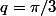
, on a :
=1/2)
et
=sqrt{3}/2)
d'ou
}{2} = sin(\pi/6)-sin(\pi/3) = 2cos(\pi/4)sin(-\pi/6) = -cos(\pi/4)=cos(\pi-\pi/4)=cos(3\pi/4))
et finalement :
}{2}) = Arcos(cos(3\pi/4))=3\pi/4)
On m'a signalé que je me suis trompé ! Mon résultat est faux...
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Nov 2006, 23:09
par yos » 24 Nov 2006, 23:09
tize a écrit:sin(-\pi/6) = -cos(\pi/4))
C'est là que ça pêche.
Mais j'ai pas mieux. Si un cosinus simple valait

, on nous aurait prévenu je pense.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 25 Nov 2006, 01:37
par aviateurpilot » 25 Nov 2006, 01:37
=\frac{1-\sqrt{3}}{2})
=2cos(a))
(il se peux que cela vous donne une idée :zen: )
on bien on calcule
,cos(2a),....,cos(ka),..)
jusqu'a ce qu'on trouve une valeur usuel.
car je ne pense pas que

irrationnel.
c-a-dire, qu'il existe p tel que
=1)
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 25 Nov 2006, 09:02
par Quidam » 25 Nov 2006, 09:02
aviateurpilot a écrit:=\frac{1-\sqrt{3}}{2})
=2cos(a))
(il se peux que cela vous donne une idée :zen: )
on bien on calcule
,cos(2a),....,cos(ka),..)
jusqu'a ce qu'on trouve une valeur usuel.
car je ne pense pas que

irrationnel.
c-a-dire, qu'il existe p tel que
=1)
Un peu brouillon... A revoir !
aviateurpilot a écrit:=\frac{1-\sqrt{3}}{2})
=2cos(a))
??? Et pourquoi donc ?
aviateurpilot a écrit:que

irrationnel.
c-a-dire, qu'il existe p tel que
=1)
.
Explique nous pourquoi "

irrationnel" signifierait "
=1)
"
Ou alors, j'ai mal lu !
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 25 Nov 2006, 09:59
par Zebulon » 25 Nov 2006, 09:59
Quidam a écrit:Explique nous pourquoi "

irrationnel" signifierait "
=1)
"
Pour moi, il dit le contraire :

serait rationnel donc il existerait p tel que cos(pa)=1.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 25 Nov 2006, 12:09
par aviateurpilot » 25 Nov 2006, 12:09
Quidam a écrit:=\frac{1-\sqrt{3}}{1})
=cos(2a))
j'ai voulu ecrire
=\frac{1-\sqrt{3}}{1})
=>
)
solution de
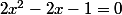
=>
-1=2cos(a))
=>
=cos(2a))
Zebulon a écrit:Pour moi, il dit le contraire :

serait rationnel donc il existerait p tel que cos(pa)=1.
exactement.
tt simplment car dans ce cas il existe
\in N^2)
tel que
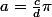
(pour
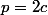
,
=1)
)
is on essaye de calculer
 puis cos(2a)...cos(ka))
on peux meme avant d'arriver a
=1)
trouver une valeur usuel {

} ou bien une valeur d'un angle que tu connais comme
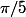
,....etc
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 25 Nov 2006, 12:33
par alben » 25 Nov 2006, 12:33
Bonjour Aviateurpilot
D'accord, la propiriété cos(2a)=2cos(a) est vraie et troublante mais tu t'avances beaucoup en induisant que a/pi est rationnel.
C'est possible mais improbable (compte tenu de la rareté des rationnels dans R)
En tout cas, je peux affirmer que si cette valeur s'écrit sous la forme p/q, p et q dépassent 5 millions. Ce sont en effet les limites de précision de ma décomposition en fractions rationnelles effectuée sur excel.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
) parce que personnellement je sèche...
=\frac{1-\sqrt{3}}{2})
jusqu'a ce qu'on trouve une valeur usuel.
irrationnel.
=\frac{1-\sqrt{3}}{2})
irrationnel.
.
=\frac{1-\sqrt{3}}{1})
serait rationnel donc il existerait p tel que cos(pa)=1.