Petit probleme

par **bastien83** » 26 Oct 2006, 08:24

bonjour,

je cherche à trouver le signe de

je n'arrive pas à trouve rla valeur qui s'annule et dc qui marque la limite entre le cote + et le cote -

merci d'avance

par **Dominique Lefebvre** » 26 Oct 2006, 08:33

bastien83 a écrit:bonjour,

je cherche à trouver le signe de

je n'arrive pas à trouve rla valeur qui s'annule et dc qui marque la limite entre le cote + et le cote -

merci d'avance

Bonjour,

Tu veux bien réviser ton cours d'analyse....
g' est la somme de deux exponentielles. Que sais-tu de la valeur d'une fonction exponentielle? Que penses-tu du signe de la somme de deux exponentielles?

par **fonfon** » 26 Oct 2006, 08:34

salut,

et en appliquant la fonction logarithme on obtient:

.....

par **johnjohnjohn** » 26 Oct 2006, 08:41

bastien83 a écrit:bonjour,

je cherche à trouver le signe de

je n'arrive pas à trouve rla valeur qui s'annule et dc qui marque la limite entre le cote + et le cote -

merci d'avance

Peut être pourrais tu commencer par factoriser ( c'est le plus souvent un réflexe salvateur en maths ) pour y voir clair :

Puis posant

tu nous termines le boulot ...

par **bastien83** » 26 Oct 2006, 09:11

Dominique Lefebvre a écrit:Bonjour,

Tu veux bien réviser ton cours d'analyse....
g' est la somme de deux exponentielles. Que sais-tu de la valeur d'une fonction exponentielle? Que penses-tu du signe de la somme de deux exponentielles?

je sais qu un expo n'est jamais negatif .
la somme des 2 expo est dc -si

la premiere partie est sup à la deuxieme

par **bastien83** » 26 Oct 2006, 09:28

johnjohnjohn a écrit:Peut être pourrais tu commencer par factoriser ( c'est le plus souvent un réflexe salvateur en maths ) pour y voir clair :

Puis posant

tu nous termines le boulot ...

je trouve X=1/2

donc x=

c'est exacte??

par **johnjohnjohn** » 26 Oct 2006, 09:33

bastien83 a écrit:je trouve X=1/2

donc x=
c'est exacte??

Non hélas

Tu ne t'en sortiras pas sans apprendre ton cours sur la fonction exponentielle et la fonction logarithme et de toute évidence tu ne le maitrises pas.

par **bastien83** » 26 Oct 2006, 09:36

je n'ia pas encore appris les logarithme.
en ce qui concerne les expo j'ai appris mon cours mais c'est vrai que j'ai un peu de mal

mon X est il bon ??

par **fonfon** » 26 Oct 2006, 09:39

Re, sans la fonction logarithme je ne vois pas comment tu peux t'en sortir c'est quoi au juste ta fonction g(x)

par **bastien83** » 26 Oct 2006, 09:43

j'ai :
g(x)=

g'(x)=

g"(x)=

voila

par **fonfon** » 26 Oct 2006, 09:58

salut, je pourrais avoir la question complete ?

et je suis pas trops d'accord avec g'(x):

donc g''(x) n'est pas bon

par **johnjohnjohn** » 26 Oct 2006, 10:03

bastien83 a écrit:j'ai :
g(x)=
g'(x)=
g"(x)=
voila

Bon tout ceci est juste. ( C'est toi qui a déterminé g' et g'' ? ). Effectivement s'il s'agit de determiner les variations de g, tu t'en sors sans les log. Il y a juste que tu ne pourras pas expliciter la valeur de x qui annule g'. L'idée, c'est de dire que

g''(x) > 0 pour tout x de l'ensemble de definition de g ( qui est hein ??? )
g' est donc strictement croissante sur cet ensemble de def . Comme t'as les limites de g' aux extrémités de cet ensemble de def et que la fonction g' est continue ....
On te laisse dresser le tableau de variation

Pour le X oui tu as raison mais sans connaître la fonction log ( c'est étonnant quand même ) et donc expliciter x, tu dois pouvoir parler de la valeur alpha tel que g'(alpha) = 0

Hope this help

par **johnjohnjohn** » 26 Oct 2006, 10:11

johnjohnjohn a écrit:Bon tout ceci est juste. ( C'est toi qui a déterminé g' et g'' ? ). Effectivement s'il s'agit de determiner les variations de g, tu t'en sors sans les log. Il y a juste que tu ne pourras pas expliciter la valeur de x qui annule g'. L'idée, c'est de dire que

g''(x) > 0 pour tout x de l'ensemble de definition de g ( qui est hein ??? )
g' est donc strictement croissante sur cet ensemble de def . Comme t'as les limites de g' aux extrémités de cet ensemble de def et que la fonction g' est continue ....
On te laisse dresser le tableau de variation

Pour le X oui tu as raison mais sans connaître la fonction log ( c'est étonnant quand même ) et donc expliciter x, tu dois pouvoir parler de la valeur alpha tel que g'(alpha) = 0

Hope this help

Oui fonfon a raison pour les calculs, les tiens sont finalement faux . Retiens juste la démarche que je t'ai indiquée.

par **bastien83** » 26 Oct 2006, 10:15

johnjohnjohn a écrit:Bon tout ceci est juste. ( C'est toi qui a déterminé g' et g'' ? ). oui c'est moi mais d'apres fonfon c'est faux donc je verifie Effectivement s'il s'agit de determiner les variations de g, tu t'en sors sans les log. Il y a juste que tu ne pourras pas expliciter la valeur de x qui annule g'. L'idée, c'est de dire que

g''(x) > 0 pour tout x de l'ensemble de definition de g ( qui est hein ??? )
g' est donc strictement croissante sur cet ensemble de def . Comme t'as les limites de g' aux extrémités de cet ensemble de def et que la fonction g' est continue ....
On te laisse dresser le tableau de variation
pour ca, je l'ai fait

Pour le X oui tu as raison mais sans connaître la fonction log ( c'est étonnant quand même ) et donc expliciter x, tu dois pouvoir parler de la valeur alpha tel que g'(alpha) = 0
je fais dc comment pour faire mon tableau de variation
Hope this help

voila

en se qui concerne mon g'(x) je trouve

-

par **fonfon** » 26 Oct 2006, 10:27

Re, si c'est g'(x) c'est pas bon c'est:

je refait le calcul:

Ps

donc je reviens à g'(x):je mets e^(-2x) en facteur

par **bastien83** » 26 Oct 2006, 10:41

je susi d'accord avec vous j'ai du faire une erreur de calcule.
dc
g"(x)=8xe^-2x

par **johnjohnjohn** » 26 Oct 2006, 10:42

bastien83 a écrit:voila

en se qui concerne mon g'(x) je trouve

-

En fait j'avais fait confiance à tes calculs faux. Mais cette valeur de alpha dont je t'ai parlé vu la tronche de ta fonction g' ( la bonne ) tu vas être en mesure de l'expliciter ( une fois que tu auras fait les calculs corrects de g' et g'' )

par **fonfon** » 26 Oct 2006, 10:55

Re,

il doit y avoir encore une erreur de calcul

avec tu devrais pouvoir trouver le tableau de variation de g'(x) et en deduire celui de g(x)

par **bastien83** » 26 Oct 2006, 11:53

j'avais pris la fonction d'un bloc est non comme u*v

par **bastien83** » 26 Oct 2006, 12:04

re,

je cherche à trouver le signe de

g'(x) mais j'en suis pas tres sur:

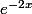
ne s'annule pas
dc
-4x=0
x=0

c'est exacte?????

Petit probleme

petit probleme

Qui est en ligne