Bonjour !
J'ai une formule de credit-bail dans laquelle je voudrais isoler le i
correspondant à l'interet .
PMT = (pv -(fv/(1+i)^n)) * i / ((1+i)-(1+i)^(1-n))
donc voila ..
i = ???
Merci de votre aide :)
Isoler un inconnu d'une formule
21 messages
- Page 1 sur 2 - 1, 2
par Geremzzz » 13 Sep 2006, 14:11
Je viens de me rendre compte que ce n'est peut etre pas de niveau superieur , j'ai honte d'avoir oublier tout se que j'ai fait au lycée ;)
par Geremzzz » 13 Sep 2006, 14:58
J'ai pas précisé dans le titre car on a pas le droit mais mais c'est super urgent :D
par nox » 13 Sep 2006, 15:45
J'ai pas trop regardé et pas le temps de me lancer dans les calculs...mais si tu veux une valeur approchée y a moultes méthodes pour trouver ça : dichotomie, point fixe etc...
si tu veux calculer la valeur analytiquement ba faut voir si y a moyen de s'en sortir en finesse...
si tu veux calculer la valeur analytiquement ba faut voir si y a moyen de s'en sortir en finesse...
par Geremzzz » 13 Sep 2006, 15:53
Je suis trop une quiche en math pour pouvoir retrouver i, en effet il ne me faut que la formule pour trouver l'interet.
par tize » 13 Sep 2006, 16:44
Je résume, on a :
^n}\right)\times\frac{i}{(1+i)-(1+i)^{(1-n)}})
Question : Je ne sais pas ce que veut dire
mais y a-t-il une chose à savoir qui pourrait donner un lien supplémentaire entre ses paramètres ?
Question : Je ne sais pas ce que veut dire
par Quidam » 13 Sep 2006, 16:57
Je connais une formule plus simple donnant les remboursements périodiques d'un capital C dans le cas d'un versement constant égal à R sur n périodes, avec un taux t:
^{-n}})
Mis à part les noms de variables différents (l'un de nous deux doit s'adapter à l'autre, et le hasard t'a désigné !), et le -fv qui je pense représente la valeur restant due après n remboursements (et qui est donc absent de ma formule car il faut avoir tout remboursé pour récupérer son hypothèque :zen: ) les deux formules diffèrent encore par un coefficient (1+i) dans ta formule, que je ne parviens pas à comprendre.
Cependant, ma formule est donc beaucoup plus simple que la tienne et malgré cela il est impossible de calculer t (l'équivalent de ton i) directement, alors qu'au contraire on peut calculer directement R si l'on a C,n et t, calculer C si l'on a R ,n et t, calculer n si l'on a R, C et t.
La seule méthode que je connaisse, est de faire une itération en partant d'une valeur approximative de t (pour toi de i) d'isoler le i se trouvant au numérateur tout seul dans ta formule (mais en laissant les autres i : appelons les i0) et de calculer i en fonction de i0, puis de refaire l'opération en donnant à i0 cette fois la nouvelle valeur calculée de i. Au bout de 20 (si n=200) ou 200 (si n=20) itérations, la nouvelle valeur calculée de i est presque égale à i0 et on s'arrête à ce moment. Dans le cas de ma formule par exemple, on écrit la formule ci-dessus :
^{-n})}{C})
on se donne un
approximatif, et on calcule t qu'on réinjecte dans pour le calcul suivant etc...
Donc, on ne peut pas calculer directement par i=...
Mis à part les noms de variables différents (l'un de nous deux doit s'adapter à l'autre, et le hasard t'a désigné !), et le -fv qui je pense représente la valeur restant due après n remboursements (et qui est donc absent de ma formule car il faut avoir tout remboursé pour récupérer son hypothèque :zen: ) les deux formules diffèrent encore par un coefficient (1+i) dans ta formule, que je ne parviens pas à comprendre.
Cependant, ma formule est donc beaucoup plus simple que la tienne et malgré cela il est impossible de calculer t (l'équivalent de ton i) directement, alors qu'au contraire on peut calculer directement R si l'on a C,n et t, calculer C si l'on a R ,n et t, calculer n si l'on a R, C et t.
La seule méthode que je connaisse, est de faire une itération en partant d'une valeur approximative de t (pour toi de i) d'isoler le i se trouvant au numérateur tout seul dans ta formule (mais en laissant les autres i : appelons les i0) et de calculer i en fonction de i0, puis de refaire l'opération en donnant à i0 cette fois la nouvelle valeur calculée de i. Au bout de 20 (si n=200) ou 200 (si n=20) itérations, la nouvelle valeur calculée de i est presque égale à i0 et on s'arrête à ce moment. Dans le cas de ma formule par exemple, on écrit la formule ci-dessus :
on se donne un
Donc, on ne peut pas calculer directement par i=...
par alben » 13 Sep 2006, 16:59
Bonsoir,
En développant la formule, on tombe sur une équation de degré n+1 et comme n est probablement supérieur à 3, il n'existe pas de formule pour trouver i.
Il faut donc utiliser une méthode numérique comme le suggère nox.
Le plus simple consiste à programmer le calcul de PMT sur excel (ou autre) et à procéder par essais successifs
En développant la formule, on tombe sur une équation de degré n+1 et comme n est probablement supérieur à 3, il n'existe pas de formule pour trouver i.
Il faut donc utiliser une méthode numérique comme le suggère nox.
Le plus simple consiste à programmer le calcul de PMT sur excel (ou autre) et à procéder par essais successifs
par Geremzzz » 14 Sep 2006, 09:08
Merci pour vos réponses, meme si j'ai du mal à tout saisir, je comprend mieux mon problème, je vais essayer de me débrouiller avec ca..
Encore merci !
Encore merci !
par nox » 14 Sep 2006, 09:11
Google -> dichotomie
-> point fixe
-> sécante
-> Newton Raphson
-> quasi Newton
-> ....
-> point fixe
-> sécante
-> Newton Raphson
-> quasi Newton
-> ....
par Quidam » 14 Sep 2006, 11:37
En fait, j'ai quelques doutes sur ta formule ; disons plutôt que je ne comprends pas bien à quoi correspond PMT (est-ce PMT pour paiement ?). Je parviens presque à retrouver ta formule, comme tu vas le voir ici. J'ai renommé tes variables : j'appelle C un capital emprunté au taux t par période, remboursé partiellement en n périodes avec une somme constante R à la fin de chaque période. J'ai mis en gras "à la fin" car je soupçonne que PMT serait plutôt un paiement au début de chaque période ! (je trouve cela très illogique, car à quoi cela sert-il de préter C à une personne s'il doit immédiatement rembourser une partie de C, mais bon ...il se trouve que c'est ma seule explication à la différence entre la formule à laquelle j'aboutis et ta formule !)
Après une période on rembourse R. On peut considérer quon rembourse une certaine partie
du capital C avec ses intérêts. Comme une seule période sest écoulée cette somme est devenue )
et cest cela quon paie. Donc )
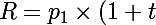et 
. Ce qui reste dû, cest la partie du capital qui na pas encore été remboursée, cest-à-dire 
, partie qui a elle aussi été productrice dintérêt. Donc la somme \times (1+t))
reste due.
Faisons le bilan :
Après une période : la somme restant due est : soit \times (1+t)=C\times(1+t)-R)
Je sais bien que pour le public non averti (ce qui inclut les guichetiers de ma banque), on ne présente pas les choses comme cela. On préfère dire quon doit payer les intérêts du capital total C sur une période, soit Ct, et quon diminuera le capital ensuite de la différence entre le remboursement R et ces intérêts. Cela se traduit par :
Intérêts sur la période : Ct
Partie du capital remboursée : R-Ct
Capital restant dû après une période : C (R-Ct) = C(1+t)-R
On constate évidemment que les deux façons de voir les choses sont strictement identiques : dans les deux cas la somme restant due après une période est la même :-R)
. Simplement la banque dit que je dois un capital de C(1+t)-R et que je nai pas dintérêts en retard, alors que moi je dis quil me reste à régler une part )
du capital initial, avec ses intérêts sélevant à t)
. Le total est le même : largent na pas dodeur, un sou est un sou.
La raison pour laquelle je préfère mon approche, est que dans ce cas le calcul devient très très simple. Je continue.
Après deux périodes, on rembourse R. On peut considérer quon rembourse une certaine partie
du capital C avec ses intérêts. Comme deux périodes se sont écoulées cette somme est devenue ^2)
et cest cela quon paie. Donc 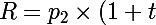^2)
et ^2})
. Ce qui reste dû, cest la partie du capital qui na pas encore été remboursée, cest-à-dire 
, partie qui a elle aussi été productrice dintérêt. Donc la somme \times (1+t)^2)
reste due.
On note que
, que et de façon générale ^k})
quelle que soit la période k.
Et ainsi de suite pendant n périodes.
Au bout de n périodes la somme restant due est donc :
\times (1+t)^n)
Mais il se trouve que les
sont une suite géométrique, dont chacun sait quil est facile dévaluer la somme ! Appelons S cette somme.
^k})
Pour faciliter la lecture, je vais éviter les signes de sommation. On peut réécrire comme ceci :
^1}+\frac{R}{(1+t)^2}+\frac{R}{(1+t)^3}+\cdots +\frac{R}{(1+t)^n})
^n}[(1+t)^{n-1}+(1+t)^{n-2}+(1+t)^{n-3}+\cdots +1])
^n}[\frac{(1+t)^n-1}{(1+t)-1}])
^n}[\frac{(1+t)^n-1}{t}])
Reprenant le calcul général on peut écrire que la somme restant due au bout de n périodes est :
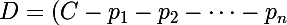\times (1+t)^n)
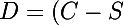\times (1+t)^n)
^n}[\frac{(1+t)^n-1}{t}])\times (1+t)^n)
On s'aperçoit alors que cette formule peut être manipulée jusqu'à ressembler étrangement à la tienne, à condition de changer les noms de variables...
^n}[\frac{(1+t)^n-1}{t}])\times (1+t)^n)
^n} = C-\frac{R}{(1+t)^n}[\frac{(1+t)^n-1}{t}]))
^n} = \frac{R}{t}\times (1-(1+t)^{-n}))
^n}) = R\times (1-(1+t)^{-n}))
^n})}{1-(1+t)^{-n}})
^n})}{(1+t)-(1+t)^{1-n}})
On voit que non pas R mais})
semble exactement égal à la variable PMT de ta formule, à condition d'appeler D "fv" (comme future value ?), d'appeler t "i", d'appeler C "pv" (comme present value ?) :
^n})}{(1+i)-(1+i)^{1-n}})
ou
^n})\times \frac{i}{(1+i)-(1+i)^{1-n}})
Ceci est donc à comparer à ta formule :
^n})\times \frac{i}{(1+i)-(1+i)^{1-n}})
Il semble donc que ce que j'appelle R est égal à)
et ceci correspondrait à un paiement FMT qui serait fait au début de chaque période et non à la fin.
Quoi qu'il en soit, je pense que ma première réponse reste valable. En écrivant la formule comme ceci :
-(1+i)^{-n}}{pv-\frac{fv}{(1+i)^n}})
et en réécrivant en donnant deux noms différents
et 
aux termes i de la formule :
-(1+i_0)^{-n}}{pv-\frac{fv}{(1+i_0)^n}})
Puis, de façon plus générale, en considérant la suite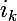
, définie par :
-(1+i_k)^{-n}}{pv-\frac{fv}{(1+i_k)^n}})
On définit une suite qui sera convergente si le premier terme que tu dois choisir au départ n'est "pas trop éloigné" de la solution. Et la limite de cette suite sera la valeur i que tu cherches.
Mon expérience m'a appris que la suite convergeait vite (une dizaine ou une vingtaine d'itérations) si n est grand (ex: 180 mensualités), et assez lentement pour un prêt à court terme (24 mensualités). En tout état de cause, l'usage d'une calculatrice programmable ou d'un PC ma semble précieux, parce faire 200 itérations de tels calculs à la main, c'est dur !
Après une période on rembourse R. On peut considérer quon rembourse une certaine partie
Faisons le bilan :
Après une période : la somme restant due est :
Je sais bien que pour le public non averti (ce qui inclut les guichetiers de ma banque), on ne présente pas les choses comme cela. On préfère dire quon doit payer les intérêts du capital total C sur une période, soit Ct, et quon diminuera le capital ensuite de la différence entre le remboursement R et ces intérêts. Cela se traduit par :
Intérêts sur la période : Ct
Partie du capital remboursée : R-Ct
Capital restant dû après une période : C (R-Ct) = C(1+t)-R
On constate évidemment que les deux façons de voir les choses sont strictement identiques : dans les deux cas la somme restant due après une période est la même :
La raison pour laquelle je préfère mon approche, est que dans ce cas le calcul devient très très simple. Je continue.
Après deux périodes, on rembourse R. On peut considérer quon rembourse une certaine partie
On note que
Et ainsi de suite pendant n périodes.
Au bout de n périodes la somme restant due est donc :
Mais il se trouve que les
Pour faciliter la lecture, je vais éviter les signes de sommation. On peut réécrire comme ceci :
Reprenant le calcul général on peut écrire que la somme restant due au bout de n périodes est :
On s'aperçoit alors que cette formule peut être manipulée jusqu'à ressembler étrangement à la tienne, à condition de changer les noms de variables...
On voit que non pas R mais
ou
Ceci est donc à comparer à ta formule :
Il semble donc que ce que j'appelle R est égal à
Quoi qu'il en soit, je pense que ma première réponse reste valable. En écrivant la formule comme ceci :
et en réécrivant en donnant deux noms différents
Puis, de façon plus générale, en considérant la suite
On définit une suite qui sera convergente si le premier terme
Mon expérience m'a appris que la suite convergeait vite (une dizaine ou une vingtaine d'itérations) si n est grand (ex: 180 mensualités), et assez lentement pour un prêt à court terme (24 mensualités). En tout état de cause, l'usage d'une calculatrice programmable ou d'un PC ma semble précieux, parce faire 200 itérations de tels calculs à la main, c'est dur !
par alben » 14 Sep 2006, 12:55
Bonjour,
Pour Quidam
Tu ne dois pas te tourmenter pour le 1+t excédentaire, ce type de calcul ne se rencontre pas que dans les calculs d'intérêt sur emprunts mais également pour estimer le rendement d'un placement : PMT peut vouloir dire placement mensuel ou profit....
On pourrait construire une histoire cohérente où PV serait le prix d'acquisition, fv la valeur de revente
NB comme valeur de départ, il peut être judicieux de prendre le taux correspondant à des intérêts simples
Pour Quidam
Tu ne dois pas te tourmenter pour le 1+t excédentaire, ce type de calcul ne se rencontre pas que dans les calculs d'intérêt sur emprunts mais également pour estimer le rendement d'un placement : PMT peut vouloir dire placement mensuel ou profit....
On pourrait construire une histoire cohérente où PV serait le prix d'acquisition, fv la valeur de revente
NB comme valeur de départ, il peut être judicieux de prendre le taux correspondant à des intérêts simples
par Quidam » 15 Sep 2006, 10:42
alben a écrit:Bonjour,
Pour Quidam
Tu ne dois pas te tourmenter pour le 1+t excédentaire, ce type de calcul ne se rencontre pas que dans les calculs d'intérêt sur emprunts mais également pour estimer le rendement d'un placement : PMT peut vouloir dire placement mensuel ou profit....
On pourrait construire une histoire cohérente où PV serait le prix d'acquisition, fv la valeur de revente
NB comme valeur de départ, il peut être judicieux de prendre le taux correspondant à des intérêts simples
Merci pour l'info alben !
par Geremzzz » 18 Sep 2006, 09:22
Désoler de ne pas vous avoir répondu plutot mais j'etais en deplacement..
PMT est le loyer a payer par periode, c'est a dire par mois, trimestre, semestre... c'est en applicant un coefficiant sur i que l'on modifie de loyer en fonction de la periode -> i mensuel = I /12 % , trimestriel i=I/4 etc ...
Il y a deux maniere de calculer un remboursement, soit a terme echu soit a terme à echoir. Un coefficient (1+i) sera ajouter dans le cas d'un paiement en fin de periode.
La formule que j'ai proposé au début est la seule me permettant de retrouver le resultat équivalent à celui la calculette financière de mon client.
Je vais relire ta réponse Quidam car tout n'est pas évident pour moi :D
Merci encore
PMT est le loyer a payer par periode, c'est a dire par mois, trimestre, semestre... c'est en applicant un coefficiant sur i que l'on modifie de loyer en fonction de la periode -> i mensuel = I /12 % , trimestriel i=I/4 etc ...
Il y a deux maniere de calculer un remboursement, soit a terme echu soit a terme à echoir. Un coefficient (1+i) sera ajouter dans le cas d'un paiement en fin de periode.
La formule que j'ai proposé au début est la seule me permettant de retrouver le resultat équivalent à celui la calculette financière de mon client.
Je vais relire ta réponse Quidam car tout n'est pas évident pour moi :D
Merci encore
par Geremzzz » 18 Sep 2006, 09:31
Qu'entend tu par limite de la suite, le moment ou n arrive au terme du pret?
Je ne comprend pas comment en utilisant un i0 approximatif on peut arriver a un i juste ...
Je ne comprend pas comment en utilisant un i0 approximatif on peut arriver a un i juste ...
par Geremzzz » 18 Sep 2006, 10:58
une question de plus :
est-ce que les itérations correspondent à n ??
En lisant les réponses je pense que non, donc quel est le rapport entre n et
le nb d'itérétion car je ne comprend pas le :
"Au bout de 20 (si n=200) ou 200 (si n=20) itérations..."
est-ce que les itérations correspondent à n ??
En lisant les réponses je pense que non, donc quel est le rapport entre n et
le nb d'itérétion car je ne comprend pas le :
"Au bout de 20 (si n=200) ou 200 (si n=20) itérations..."
par Geremzzz » 19 Sep 2006, 22:13
Je te remercie Quidam pour tes lumières :id:
En fait je ne fais absolument pas de finances,
je suis admin réseau et programmeur à mes heures perdues
et une société de finance ma demandé un programme
réalisant tout le binzz que j'ai soumis dans ce forum.
Voilà pourquoi je suis légèrement à la rue :)
Vu le temps que j'ai pour réaliser cet outils je n'ai pas le temps
de me plonger dans des bouquins, des gens brillants existent autant
leur demander conseil !
Pour l'instant j'ai programmé (en php/javascript)
un outil de calcul de crédit-bail linéaire et dégressif
( au passage quand je parlais de diviser i par 12 ou 4 ... suivant
les echèances de loyer, c'etait évidement pour la premiere formule
que je t'ai donné : si i faisait 5% annuel, il fera i / 12 -> 0.416 % mensuel, cela fonctionne tres bien.)
Il me reste donc a faire un outil pour connaitre ce maudit tax en linéaire et en dégressif lorsque l'on a les autres variables.
Si tu as le temps de te pencher sur cet exemple et me dire combien tu trouve
pour i , avec le detail des 2 premières et 2 dernières itérations cela m'interesserais ;)
Pv = 30000 (capital emprunté)
PMT = 688,93 (remboursement mensuel)
n = 48 (terme)
fv = 300 (option d'achat de 1% du capital emprunté)
4< i <6 je sais pas si ma fourchette convient
J'en demande peut etre trop mais au dela de ce projet j'aimerais vraiment
maitriser un peu plus le sujet.
PS : dans mon programme comment automatiser le choix du nombre d'itérations nécessaires pour trouver i...
Merci again
En fait je ne fais absolument pas de finances,
je suis admin réseau et programmeur à mes heures perdues
et une société de finance ma demandé un programme
réalisant tout le binzz que j'ai soumis dans ce forum.
Voilà pourquoi je suis légèrement à la rue :)
Vu le temps que j'ai pour réaliser cet outils je n'ai pas le temps
de me plonger dans des bouquins, des gens brillants existent autant
leur demander conseil !
Pour l'instant j'ai programmé (en php/javascript)
un outil de calcul de crédit-bail linéaire et dégressif
( au passage quand je parlais de diviser i par 12 ou 4 ... suivant
les echèances de loyer, c'etait évidement pour la premiere formule
que je t'ai donné : si i faisait 5% annuel, il fera i / 12 -> 0.416 % mensuel, cela fonctionne tres bien.)
Il me reste donc a faire un outil pour connaitre ce maudit tax en linéaire et en dégressif lorsque l'on a les autres variables.
Si tu as le temps de te pencher sur cet exemple et me dire combien tu trouve
pour i , avec le detail des 2 premières et 2 dernières itérations cela m'interesserais ;)
Pv = 30000 (capital emprunté)
PMT = 688,93 (remboursement mensuel)
n = 48 (terme)
fv = 300 (option d'achat de 1% du capital emprunté)
4< i <6 je sais pas si ma fourchette convient
J'en demande peut etre trop mais au dela de ce projet j'aimerais vraiment
maitriser un peu plus le sujet.
PS : dans mon programme comment automatiser le choix du nombre d'itérations nécessaires pour trouver i...
Merci again
par Geremzzz » 19 Sep 2006, 23:06
Désolé jai donné une fourchette pour un i annuel
meme si je pense que tu l'aurais deviné seul voici la bonne
fourchette 0,25%< i <0,65%
meme si je pense que tu l'aurais deviné seul voici la bonne
fourchette 0,25%< i <0,65%
par Quidam » 20 Sep 2006, 10:16
Geremzzz a écrit:Pv = 30000 (capital emprunté)
PMT = 688,93 (remboursement mensuel)
n = 48 (terme)
fv = 300 (option d'achat de 1% du capital emprunté)
4 \varepsilon[/TEX]Geremzzz a écrit:PS : dans mon programme comment automatiser le choix du nombre d'itérations nécessaires pour trouver i...
Le critère d'arrêt est donné par
Dans mon programme, j'ai pris
Voici un extrait de l'output du programme :
- Code: Tout sélectionner
Valeur de départ pour i : 0.0025000000000000001
Itération 1 : i=0.0026235027408522192
Itération 2 : i=0.0027451693735981437
Itération 3 : i=0.0028643299124817938
...
Itération 20 : i=0.0041961440874092263
...
Itération 50 : i=0.0045678787404564306
...
Itération 100 : i=0.0045829763218361982
...
Itération 200 : i=0.0045830357057733105
...
Itération 260 : i=0.0045830357066777442
Itération 261 : i=0.0045830357066779419
Itération 262 : i=0.0045830357066779471
Itération 263 : i=0.0045830357066779471
Après paiement n° 1 reste dû début période : 29311.070000000000 fin période : 29445.403680410938
Après paiement n° 2 reste dû début période : 28756.473680410938 fin période : 28888.265626086406
Après paiement n° 3 reste dû début période : 28199.335626086406 fin période : 28328.574188165356
...
Après paiement n°46 reste dû début période : 1664.358168228030 fin période : 1671.985981141720
Après paiement n°47 reste dû début période : 983.055981141720 fin période : 987.561361804956
Après paiement n°48 reste dû début période : 298.631361804956 fin période : 299.999999999242
En ce qui concerne la valeur de départ, dont j'ai dit qu'elle ne devait pas être "trop éloignée" de la valeur finale, il semble que j'aie fait erreur sur ce point. Le calcul ci-dessus est obtenu avec une valeur de départ arbitraire égale à i=0.0025, la borne inférieure de la fourchette que tu m'avais donnée. Mais j'ai essayé avec des valeurs de plus en plus grandes de i (0.01, puis 1, puis 10 (ce qui correspond à du 1000% par mois !)), puis, de plus en plus petites (jusqu'à 0.000001) et le programme continue à marcher parfaitement. Finalement, il est possible que ça marche dans tous les cas ! Par contre, si tu pars de i=0, le programme s'arrête tout de suite sur i=0 et bien sûr, c'est faux !
par Geremzzz » 20 Sep 2006, 11:05
Quidam a encore frappé... ;)
Merci tout devient beaucoup plus clair j'espère maintenant
arriver à caler ces multiples réflexion dans un algorithme.
thx a lot
Merci tout devient beaucoup plus clair j'espère maintenant
arriver à caler ces multiples réflexion dans un algorithme.
thx a lot
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :