Air d'un ovoïde de largeur 2R et de hauteur 3R
59 messages
- Page 3 sur 3 - 1, 2, 3
la réponse
Salut à tous, un nouveau membre du forum :salut:
En fait la personne qui a posé la question me l'avait posé en MP en même temps que vous. Au départ je n'ai pas compris la construction exacte et je lui ai répondu avec des bords droits tangents, avant de comprendre l'implicite du schéma pour les bords (et l' "implicite" est à éviter dans un énoncé mathématique) :mur: : ces sont des arcs tangents aux deux autres et dont les centres sont sur l'horizontale passant par le centre du plus grand disque (et là, fallait le deviner d'après le schéma d'autant que les point de tangence sont un peu approximatifs :look: ).
Bref, en m'apercevant de cela, j'ai repris le papier et le crayon, pour m'apercevoir que c'était guère plus compliqué que pour les bords droits.
Au passage j'ai pu vérifier que pour les rayons des arcs de bords annoncés dans le schéma à savoir 3R et 2.2/3 R étaient corrects (car en fait, pour la double tangence, il y a unicité... donc il fallait que cela "colle" )
Je l'ai envoyé hier à la personne concernée :++: Je vous livre les pdf ci-dessous, pour en faire profiter tout ceux qui seraient interessés par le problème, et accessoirement pour savoir si tout est OK :lol3:
Page 1 : formule générale en fonction des 2 rayons et de la distance inter-centre
Page 2 : applications à 3 prototypes de base (merci de vérifier que je ne me suis pas trompé en appliquant la formule générale SVP :lol4: )
[CENTER]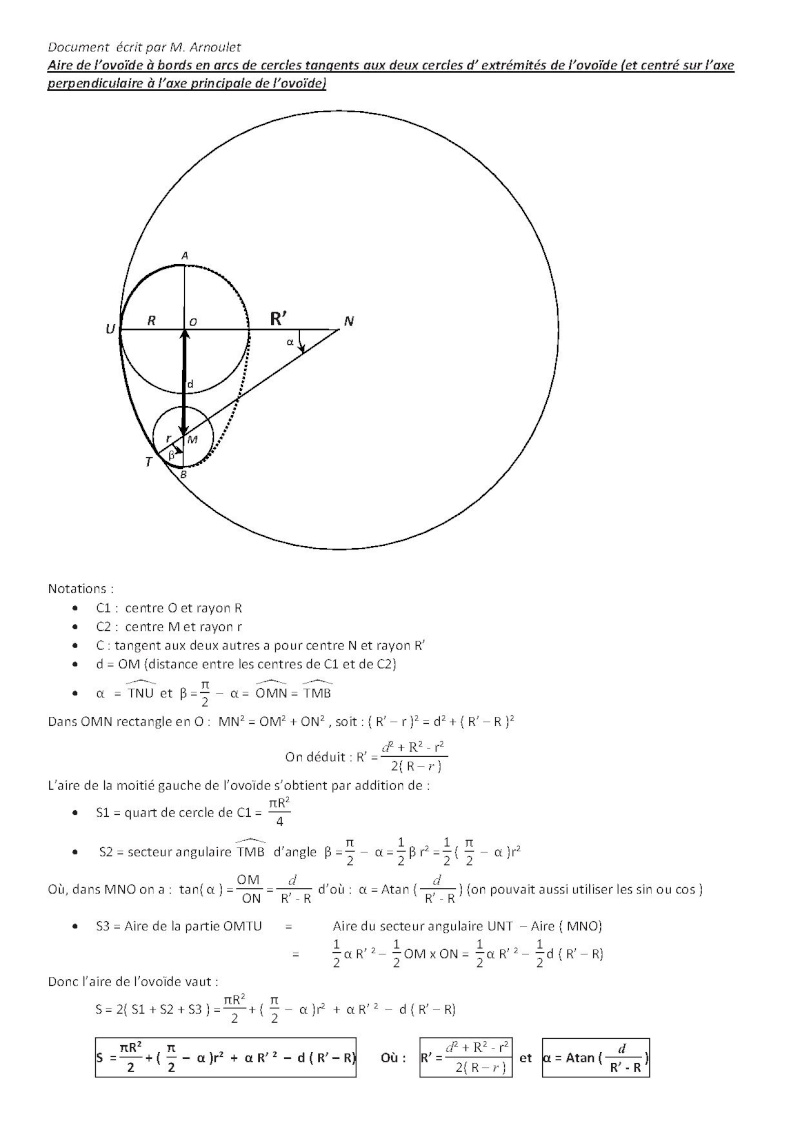
[/CENTER]
[CENTER]
[/CENTER]
Je ne connaissais pas cette méthode de génération d'ovoïde du coup, je suis content d'en avoir appris, d'autant que la forme est plutôt jolie.
Enfin, le périmètre se trouve très simplement (avec les calculs déjà effectués) :we:
Voilà :lol3:
En fait la personne qui a posé la question me l'avait posé en MP en même temps que vous. Au départ je n'ai pas compris la construction exacte et je lui ai répondu avec des bords droits tangents, avant de comprendre l'implicite du schéma pour les bords (et l' "implicite" est à éviter dans un énoncé mathématique) :mur: : ces sont des arcs tangents aux deux autres et dont les centres sont sur l'horizontale passant par le centre du plus grand disque (et là, fallait le deviner d'après le schéma d'autant que les point de tangence sont un peu approximatifs :look: ).
Bref, en m'apercevant de cela, j'ai repris le papier et le crayon, pour m'apercevoir que c'était guère plus compliqué que pour les bords droits.
Au passage j'ai pu vérifier que pour les rayons des arcs de bords annoncés dans le schéma à savoir 3R et 2.2/3 R étaient corrects (car en fait, pour la double tangence, il y a unicité... donc il fallait que cela "colle" )
Je l'ai envoyé hier à la personne concernée :++: Je vous livre les pdf ci-dessous, pour en faire profiter tout ceux qui seraient interessés par le problème, et accessoirement pour savoir si tout est OK :lol3:
Page 1 : formule générale en fonction des 2 rayons et de la distance inter-centre
Page 2 : applications à 3 prototypes de base (merci de vérifier que je ne me suis pas trompé en appliquant la formule générale SVP :lol4: )
[CENTER]

[/CENTER]
[CENTER]

[/CENTER]
Je ne connaissais pas cette méthode de génération d'ovoïde du coup, je suis content d'en avoir appris, d'autant que la forme est plutôt jolie.
Enfin, le périmètre se trouve très simplement (avec les calculs déjà effectués) :we:
Voilà :lol3:
Bonjour Beagle,
Personnellement, j'ai d'autres motivations.
D'abord, c'est pas très gentil, ni pour les membres du forum, ni pour ses organisateurs.
Moi, mes motivations sont simples, la retraite est la pire des choses, alors j'essaye de me rendre encore un peu utile.
J'explique plus en détail la cause du goût amer laissé par ce fil.
Apparemment l'initiateur a passé pas mal de temps à faire des maths, vu le niveau où il est est arrivé. Que reste-t-il de tout ce temps passé : pas grand-chose, en tout cas pas suffisamment pour analyser et résoudre un problème simple.
Les membres actifs du présent forum n'ont pas tellement mieux réussi.
Y'a pas de quoi se poser des questions?
nodjim:
" l'important est de se faire plaisir autant que possible"
+1
Perso je me sers encore de l'addition pour ma compta donc j'utilise un peu de maths.
Et sans le plaisir je serais sur ce forum par masochisme ou schizophrénie.
Personnellement, j'ai d'autres motivations.
D'abord, c'est pas très gentil, ni pour les membres du forum, ni pour ses organisateurs.
Moi, mes motivations sont simples, la retraite est la pire des choses, alors j'essaye de me rendre encore un peu utile.
J'explique plus en détail la cause du goût amer laissé par ce fil.
Apparemment l'initiateur a passé pas mal de temps à faire des maths, vu le niveau où il est est arrivé. Que reste-t-il de tout ce temps passé : pas grand-chose, en tout cas pas suffisamment pour analyser et résoudre un problème simple.
Les membres actifs du présent forum n'ont pas tellement mieux réussi.
Y'a pas de quoi se poser des questions?
cette citation de beagle est à la date du 13/02/2012 12h46mn un faux,
s'il est parti hier soir à la poubelle, fallait le laisser dedans.
Efface ton message précédent et j'efface aussi celui-ci dans quelques minutes,
merci
PS: comme Nodjim, il m'est arrivé de ne pas aimer des réflexions qui t'on été faites,
mais bon c'est pas un forum de cure psychothérapeutique ici, dès lors qu'on balance des trucs faut savoir encaisser aussi.
s'il est parti hier soir à la poubelle, fallait le laisser dedans.
Efface ton message précédent et j'efface aussi celui-ci dans quelques minutes,
merci
PS: comme Nodjim, il m'est arrivé de ne pas aimer des réflexions qui t'on été faites,
mais bon c'est pas un forum de cure psychothérapeutique ici, dès lors qu'on balance des trucs faut savoir encaisser aussi.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Retour au thème de ce topic.
Dlzlogic a écrit:D'après les deux ou trois premiers échanges de ce fil, je m'attendais plutôt à une réponse telle que celle-ci :
"Les fabricants français d'ovoïdes nous fournissent les formules de calcul, il n'en est pas de même des fabricants étrangers.
On appelle rayon hydraulique le rapport entre la section d'écoulement et le périmètre mouillé. C'est le rayon hydraulique qui entre dans le formules de calcul d'écoulement.
La formule utilisée est la formule de Chesy V = c sqrt(R.I)
V est la vitesse ; R le rayon hydraulique ; I la pente de l'ouvrage ; c un coefficient dont on connait l'expression.
Le problème se ramène donc à calculer le rayon hydraulique en fonction de la géométrie de l'ovoïde et de la hauteur d'eau dans celui-ci."
Petit résumé.bourbaky69 a écrit:"enfin"
pas sûr d'avoir tout compris mais il nous manque le périmètre P de l'ovoïde pour le calcul du rayon hydraulique n'est-ce pas ?
Un ovoïde est utilisé en assainissement d'eaux pluviales, quelques fois (rares) en unitaire.
Cette forme de "petit rayon" en bas à l'avantage d'augmenter la vitesse par temps "sec" pour faciliter l'auto-curage.
Généralement on calcule les réseaux de façon à satisfaire un écoulement gravitaire pour des débits de pointe correspondant à une certaine période de retour (10 ans, 20 ans ... 100 ans).
Le débit maximum d'un tuyau n'est pas obtenu quand il est plein. Pour un tuyau circulaire, ce maximum est obtenu avec une hauteur de remplissage égale à 80% du diamètre.
Quoi qu'il en soit, il est nécessaire de calculer la hauteur d'eau pour le débit donné, c'est à dire calculer le rayon hydraulique pour une hauteur d'eau donnée.
Par exemple, pour un tuyau circulaire, si le tuyau est rempli à moitié, la hauteur d'eau est D/2, la section d'écoulement est pi.D²/8, le périmètre mouillé est pi.D/2. D'où Rh = D/4.
En fait le but réel de la question était simplement le périmètre total, et non l'aire de la section, mais puisqu'il s'agit du forum "Défi" cette extension à la question d'origine, et correspondant à un calcul réel, me parait digne d'intérêt.
Merci pour ta réponse :lol3:
vus les calculs préalables ayant amené à l'aire, le plus difficile a été fait car je peux maintenant en utiliser quelques résultats pour le périmètre.
Je laisse le soin aux blogueurs d'appliquer cette formule dans les cas des prototypes particuliers et d'en déduire le rayon hydraulique en fonction des différents paramètres (car j'ai des choses à faire aujourd'hui, et son application est immédiate)
Comme tu le dis, il s'agit d'un défi et qu'on peut faire quelques écarts, j'ai même étudié un autre prototype particulier intéressant :id:
[CENTER]
[/CENTER]
J'espère avoir fait avancer le "smillblick"
vus les calculs préalables ayant amené à l'aire, le plus difficile a été fait car je peux maintenant en utiliser quelques résultats pour le périmètre.
Je laisse le soin aux blogueurs d'appliquer cette formule dans les cas des prototypes particuliers et d'en déduire le rayon hydraulique en fonction des différents paramètres (car j'ai des choses à faire aujourd'hui, et son application est immédiate)
Comme tu le dis, il s'agit d'un défi et qu'on peut faire quelques écarts, j'ai même étudié un autre prototype particulier intéressant :id:
[CENTER]

[/CENTER]
J'espère avoir fait avancer le "smillblick"
Dlzlogic a écrit:Oui, ça parait intéressant, mais un angle entre 2 arcs de cercle, c'est contraire à tous les impératifs liés à la résistance des matériaux. Quant à l'écoulement c'est pas vraiment génial.
Non mais là c'était pour le plaisir géométrique la goutte d'eau !!! J'imagine bien qu'un point d'inflexion n'est pas idéal pour un écoulement ou la résistance des matériaux :lol3:
La formule générale du périmètre de l'ovoïde est précisée (et encadrée...) juste avant ! (comme tu le dis, on fait des maths pour le plaisir et quand je trouve un corollaire intéressant, même HS, je ne me prive pas pour le communiquer) :lol3:
Donc j'ai donné une formule générale de l'aire ET du périmètre de l'ovoïde ( avec paramètres R, r et d) puis appliqué cette formule de l'aire dans le cas de 3 (et même maintenant 4) prototypes, et je laisse l'application de la formule générale du périmètre ci-dessus aux blogueurs dans le cas de ces 4 prototypes : suffit de remplacer r et R' et alpha en fonction de R suivant le prototype, comme je l'ai fait pour l'aire...
que manque-t-il ? :hein:
Sinon un défi en rapport direct avec le problème posé :
exprimer, en fonction de la hauteur d'eau h (rappel : la base de remplissage est côté petit-disque, en bas), l'aire de la section du liquide dans l'ovoïde, et le périmètre "mouillé" (de contact) correspondant.
Là, on aura vraiment fait le tour non ?
Allez, je sors ! :zen:
exprimer, en fonction de la hauteur d'eau h (rappel : la base de remplissage est côté petit-disque, en bas), l'aire de la section du liquide dans l'ovoïde, et le périmètre "mouillé" (de contact) correspondant.
Là, on aura vraiment fait le tour non ?
Allez, je sors ! :zen:
bourbaky69 a écrit:.... il nous manque le périmètre P de l'ovoïde pour le calcul du rayon hydraulique ....
Bonjour,
Non, les périmètres (et les sections) sont indiqués sur mon mail de dimanche dernier.
Mais j'ai bien l'impression qu'ici c'est un forum de monologues (et non de discussions).
En attendant, mes deux valeurs de sections sont identiques à celles d'un récent post.
Il est donc fort probable que mes deux valeurs de périmètres le soient aussi.
Salutations.
Frank
franky1103 a écrit:Bonjour,
Non, les périmètres (et les sections) sont indiqués sur mon mail de dimanche dernier.
Mais j'ai bien l'impression qu'ici c'est un forum de monologues (et non de discussions).
En attendant, mes deux valeurs de sections sont identiques à celles d'un récent post.
Il est donc fort probable que mes deux valeurs de périmètres le soient aussi.
Salutations.
Frank
Comme toi nouveau sur le forum, je suis un peu d'accord pour dire que quand on poste des réponses exactes, les messages qui suivent semblent l'ignorer ou mal le considérer (et que les réactions sont parfois épidemiques (voir messages...effacés par les propres rédacteurs...)... je ne parlerais pas de monologues mais de "tri ou quadri-logue"
J'ai essayé de démontrer les formules données de façon générale ( distances inter-centre) surtout qu' il y a des enjeux industriels : il ne s'agit pas de croire sur parole :lol3:, et de façon indépendantes de tes résultats car je n'aime pas prendre des résulltats pour argent comptant, afin que chacun puisse vérifier la véracité de la démonstration.
Bref, j'ai fait comme si je ne te croyais pas, et j'ai démontré moi-même et sous un angle plus général (pour trouver les 2 cas particuliers d'un coup d'un seul, et pour avoir plus de choix dans les formes)
J'ai constaté que mes résultats corroboraient avec les tiens dans les cas particuliers demandés (même si les expressions sont données sous une forme un peu différente je crois) et je dois bien reconnaître que de tout ce que j'ai lu, c'est ton message qui était le plus probant (même si je respecte toute forme de recherche). Le souci de la démonstration contribue au fait d'être entendu... c'est peut-être pour cela que, tes résultats ayant été donnés directement, certains se sont efforcés de trouver autre chose, après je sais que cela prend du temps de publier la démo.
Enfin je n'ai pas vérifié que les périmètres correspondaient pour les prototypes demandés mais je suis prèt à parier que c'est le cas :++:
Salut et bravo à toi pour ces résultats : tu as été le plus efficace !
En tout cas bien content d'avoir pu te contacter :we:
Bonjour,
Devant tant d'éloges, je suis obligé de me taper le cas général que voici: les cercles supérieur et inférieur ont un rayon respectif de R et kR (avec k<1); lovoïde a une hauteur et une largeur totales respectives de 3R et 2R; soit mR le rayon de courbure de liaison entre les deux cercles.
On doit avoir: (m-k)²=(n-1)²+(2-k)², ce qui donne: m=(5-4k)/(2-2k)
Posons: A = asn[(3-2k)/(5-6k+2k²)]/2pi = acs[(4-6k+2k²)/(5-6k+2k²)]/2pi = atn[(3-2k)/ 4-6k+2k²]/2pi
Section = (1/2).pi.R² + (1/2-2A).pi. (5-4k)²/(2-2k)²R² - (4-6k+2k²)/(2-2k) R² + (2A).pi.k²R², expression que jai la flegme de simplifier (surtout pour la gloire car section plus demandée)
Périmètre = (1/2).2pi.R + (1/2-2A).2pi.(5-4k)/(2-2k)R + (2A).2pi.kR, ou en simplifiant:
Périmètre = [(7-6k)-4(5-6k+2k²)A]/(2-2k).pi.R
Si k=1/2, on retrouve un périmètre de (4-10A).pi.R
Si k=1/4, on retrouve un périmètre de (11-29A)/3.pi.R
Ma formule a donc toutes les chances dêtre correcte.
Bonne soirée.
Frank
Devant tant d'éloges, je suis obligé de me taper le cas général que voici: les cercles supérieur et inférieur ont un rayon respectif de R et kR (avec k<1); lovoïde a une hauteur et une largeur totales respectives de 3R et 2R; soit mR le rayon de courbure de liaison entre les deux cercles.
On doit avoir: (m-k)²=(n-1)²+(2-k)², ce qui donne: m=(5-4k)/(2-2k)
Posons: A = asn[(3-2k)/(5-6k+2k²)]/2pi = acs[(4-6k+2k²)/(5-6k+2k²)]/2pi = atn[(3-2k)/ 4-6k+2k²]/2pi
Section = (1/2).pi.R² + (1/2-2A).pi. (5-4k)²/(2-2k)²R² - (4-6k+2k²)/(2-2k) R² + (2A).pi.k²R², expression que jai la flegme de simplifier (surtout pour la gloire car section plus demandée)
Périmètre = (1/2).2pi.R + (1/2-2A).2pi.(5-4k)/(2-2k)R + (2A).2pi.kR, ou en simplifiant:
Périmètre = [(7-6k)-4(5-6k+2k²)A]/(2-2k).pi.R
Si k=1/2, on retrouve un périmètre de (4-10A).pi.R
Si k=1/4, on retrouve un périmètre de (11-29A)/3.pi.R
Ma formule a donc toutes les chances dêtre correcte.
Bonne soirée.
Frank
épilogue
C'est trop bête, pour le périmètre, tout est à portée de fusil ! Allez, pour finir la "copie" et pour confronter mes résultats avec ceux annoncés par franky1103 dans les cas des 2 prototypes demandés :+: , avec, toujours en bonus la forme en amande (for the fun, of course ! ;- ) )

Remarquez que ces résultats sont tout à fait conformes, dans le cas particulier des 2 prototypes initiaux, aux résultats donnés par Frank1103 (en 1ère page). :ptdr:
Vu le nombre de calculs, je n'étais pas certain de n'avoir fait aucune erreur (étourderie ou autres), et qu'il est bon de savoir que mes résultats rejoignent ceux d'une personne ayant abordé le problème indépendamment et de façon peut-être légèrement différente. :lol3:
... mission accomplie :zen:

Remarquez que ces résultats sont tout à fait conformes, dans le cas particulier des 2 prototypes initiaux, aux résultats donnés par Frank1103 (en 1ère page). :ptdr:
Vu le nombre de calculs, je n'étais pas certain de n'avoir fait aucune erreur (étourderie ou autres), et qu'il est bon de savoir que mes résultats rejoignent ceux d'une personne ayant abordé le problème indépendamment et de façon peut-être légèrement différente. :lol3:
... mission accomplie :zen:
En tour cas, BRAVO.
Sauf erreur de ma part, c'est Nodjim qui a donné la réponse pour le première fois.
Les tuyaux représentés sont fabriqués et posés depuis une bonne cinquantaine d'années, il ne s'agit en aucun cas de prototypes.
En tour cas Altahir pourra retenir que pour un ovoïde le périmètre est un peu moins que 8 fois le grand rayon, alors que pour un tuyau circulaire, il est un peu plus de 6 fois le rayon.
Sauf erreur de ma part, c'est Nodjim qui a donné la réponse pour le première fois.
Les tuyaux représentés sont fabriqués et posés depuis une bonne cinquantaine d'années, il ne s'agit en aucun cas de prototypes.
En tour cas Altahir pourra retenir que pour un ovoïde le périmètre est un peu moins que 8 fois le grand rayon, alors que pour un tuyau circulaire, il est un peu plus de 6 fois le rayon.
Dlzlogic a écrit:Sauf erreur de ma part, c'est Nodjim qui a donné la réponse pour le première fois.
sans doute, mais j'avoue avoir un peu de mal à lire les formules sous une forme "linéaire" (faudra que je m'y habitue sur les forums) et j'ai surtout du mal à valider les résultats sans preuve formelle, de plus son résultat : 4.114R² dans le 1er cas était erroné,et OK pour le périmètre ( 7,93 R ), après que le défi initial ait été transformé en celui du périmètre, et encore pour un des deux cas...d'ailleurs je pense que des tests de fuite d'écoulement dans des tuyaux ovoïde, l'aire est importante, de même pour trouver son équivalent volumique pour un tuyau cylindrique (ce qui était en partie la problématique qui m'a été posé en MP par la personne ayant posé le défi : dans ce cas Rayon équivalent = racine(Aire/pi) d'où la nécessité de connaitre l'Aire)
De fait (pour tout dire) j'avais trouvé la réponse générale rapidement (30 min après avoir compris les implicites du schéma (bords circulaires tangents)... et là oui, j'ai compris ces implicites sur le tard, désolé pour le manque de modestie, mais la personne qui a posé le pb pourra en témoigner (je lui avais donné la réponse en MP) ), ce que je veux dire c'est que je ne cherche pas à m'approprié ce défi seulement je souligne que le plus long est de rédiger la démo. Pour cela que poster du pdf m'a semblé opportun.
Dlzlogic a écrit:Les tuyaux représentés sont fabriqués et posés depuis une bonne cinquantaine d'années, il ne s'agit en aucun cas de prototypes.
Voire même bien plus longtemps pour les égouts http://fr.wikipedia.org/wiki/Ovo%C3%AFde
La personne qui m'a posé le pb en MP l'a intitulé "prototype", du coup c'est vrai... j'ai gardé le même mots, sans trop y réfléchir...
Ce qui fait plaisir c'est que cette personne m'a dit qu'elle aurait aussi besoin de la formule générale, car il existe des ovoïdes non standards dans certains pays, donc encore une fois, même si le défi concernait du 2R sur 3R, la formule générale avec d reste pertinente dans ce contexte. Les formules que je donne répondent donc à tout type d'ovoïdes ce qui est une généralisation, du point de vue géométriques, appréciable je crois.
Dlzlogic a écrit:En tour cas Altahir pourra retenir que pour un ovoïde le périmètre est un peu moins que 8 fois le grand rayon, alors que pour un tuyau circulaire, il est un peu plus de 6 fois le rayon.
Enfin dans les exemples donnés, car cela dépend de l'espacement inter-centre d ( P tendant vers l'infini avec d bien sûr), après si on reste sur du h = 3R, c'est peut-être le cas... je laisse le soin aux blogueurs de trouver l'intervalle d'encadrement minimum du rapport P/R lorsque h = 3R (à l'aide des formules données) ... avis aux amateurs :lol3: (pour moi, j'en ai assez dit sur ce topic)
Cela dit, je vais un peu lacher l'ordi pour le moment, mais si vous êtes acharnés de défis :
http://www.maths-forum.com/showthread.php?p=810531#post810531
solde de tout compte sur les ovoïdes
Dlzlogic a écrit:En tour cas Altahir pourra retenir que pour un ovoïde le périmètre est un peu moins que 8 fois le grand rayon, alors que pour un tuyau circulaire, il est un peu plus de 6 fois le rayon.
Comme je le disais, conjecture sous l'hypothèse h = 3R.
Pour tout à fait enterrer ce topic (me concernant), si pour R fixé (donc h = 3R aussi) on admet que P est croissante avec r ( r sur [ 0 ; R [ ) (Vérifié par ordinateur, mais pas si évident analytiquement, je crois), on montre que le rapport P/R décrit l'intervalle [ pi + 5 Atan(4/3) ; 2pi + 2 [
la première borne correspondant au rapport P/R de la figure en "amande" ( lorsque r = 0 ) et la borne sup se trouve par un calcul de limite de P lorsque r tend vers R, alors P tend vers 2pi R + 2R (calcul interessant d'ailleurs ! utilisant de façon indirecte (changement de variable) la limite en 0 de tan(x)/x (vers 1 ), mais pas le temps de le rédiger), donc pour un ovoïde, avec h = 3R, le rapport P/R se situe sur [ 7,778 ; 8,283 [ environ :dodo: fini de chez fini... d'ailleurs mon défi aussi, que j'ai laissé aux blogueur quelques jours, et donc je vous donne la solution (trouvée mardi... et envie de passer à autre chose, pas envie de laisser trainer), en attendant content de voir à quel point ce problème était porteur, et demandait des outils différents :+++:
http://www.maths-forum.com/showthread.php?p=811421#post811421
Salut à tous les blogueurs
59 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
