Bonjour,
Je cherche à démontrer sans succès la relation suivante :
l'image de (x;y) par la rotation d'angle alpha et de centre (0,0) est le point (x',y') où
[B]x' = x.cos (alpha) - y.sin (alpha)
y' = x. sin (alpha) + y.cos (alpha)[/B]
Pouvez-vous m'aider à démarrer ?
Merci à vous, bonne après-midi
Rotation
9 messages
- Page 1 sur 1
Tu peux également raisonner via les nombres complexes (si tu les as vu).
Soit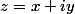 l'affixe d'un point
l'affixe d'un point  du plan et
du plan et  la rotation de centre
la rotation de centre  d'affixe
d'affixe  et d'angle
et d'angle  .
.
Alors un point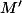 d'affixe
d'affixe 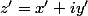 est l'image du point
est l'image du point  par la rotation
par la rotation  si et seulement si
si et seulement si  .
.
En distinguant partie réelle et partie imaginaire, tu en déduis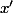 et
et 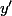 en fonction de
en fonction de  et
et  :+++:
:+++:
Soit
Alors un point
En distinguant partie réelle et partie imaginaire, tu en déduis
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Tu peux également raisonner via les nombres complexes (si tu les as vu).
Soitl'affixe d'un point
du plan et
la rotation de centre
d'affixe
et d'angle
.
Alors un pointd'affixe
est l'image du point
par la rotation
si et seulement si
.
En distinguant partie réelle et partie imaginaire, tu en déduiset
en fonction de
et
:+++:
Merci capitaine nuggets mais étant donné que je ne maitrise pas les complexes je vais essayer par d'autres biais, merci
Bonjour à tous,
J'ai cherché comme il fallait et je viens de trouver la démonstration uniquement avec des relations trigonométriques, je suis content, merci à tous pour vos idées !
http://www.cjoint.com/c/EHsirbM1wkf
Bonne journée
J'ai cherché comme il fallait et je viens de trouver la démonstration uniquement avec des relations trigonométriques, je suis content, merci à tous pour vos idées !
http://www.cjoint.com/c/EHsirbM1wkf
Bonne journée

X = L.cos(beta)
Y = L.sin(beta)
X' = L.cos(alpha+beta)
Y' = L.sin(alpha+beta)
X' = L.cos(alpha+beta) = L * (cos(alpha).cos(beta) - sin(alpha).cos(beta))
X' = L * cos(alpha).cos(beta) - L * sin(alpha).cos(beta)
X' = X.cos(alpha) - Y.sin(alpha)
Y' = L.sin(alpha+beta) = L * (sin(alpha).cos(beta) + cos(alpha).sin(beta))
Y' = L * sin(alpha).cos(beta) + L * cos(alpha).sin(beta))
Y' = X.sin(alpha) + Y.cos(alpha)
:zen:
Black Jack a écrit:
X = L.cos(beta)
Y = L.sin(beta)
X' = L.cos(alpha+beta)
Y' = L.sin(alpha+beta)
X' = L.cos(alpha+beta) = L * (cos(alpha).cos(beta) - sin(alpha).cos(beta))
X' = L * cos(alpha).cos(beta) - L * sin(alpha).cos(beta)
X' = X.cos(alpha) - Y.sin(alpha)
Y' = L.sin(alpha+beta) = L * (sin(alpha).cos(beta) + cos(alpha).sin(beta))
Y' = L * sin(alpha).cos(beta) + L * cos(alpha).sin(beta))
Y' = X.sin(alpha) + Y.cos(alpha)
:zen:
Bonjour Black Jack ainsi que tous les autres internautes,
Je maitrise bien les formules dans ce quadrant (les x>0 et les y>0 et alpha permettant de passer de M à M' dans le sens trigo),
j'aimerais maintenant pouvoir trouver les coordonnées de n'importe quel point, quelque soit le quadrant dans lequel on se trouve (x>0 ; y>0) ; (x0) ; (x0 ; y0 ou <0 aux x et/ou aux y tout en sachant que l'origine du repère du schéma de Black Jack se situe quelque part dans un autre repère, et que je souhaite trouver les coordonnées dans ce dernier......
Un exemple : http://www.cjoint.com/c/EIfplBw75vf
dans mon exemple, le repère que j'ai tracé en haut correspondrait au repère de Black Jack qui se trouve bien dans un autre repère général dans lequel je souhaite trouver les coordonnées de A,
numériquement dans mon exemple :
je connais C(5.52 ; 5.97) , B(9;4) , CA=5 et CB=4, angle C = 66.46°
je fais x'=xA = x.cos(alpha) - y.sin(alpha) = (9-5.52)cos(-66.46°) - (5.97-4)sin(-66.46°) = 3.19....
je fais une rotation en augmentant la distance donc je dois appliquer un coeff multiplicateur = 5/4 = 1.25
donc 3.19 x 1.25 = 3.9949.....et je sais par Géogebra que l'abscisse de A soit x' = 5
Ou ai-je fais une erreur ? ? ? ? ? .......MERCI pour votre aide ! ! !
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
