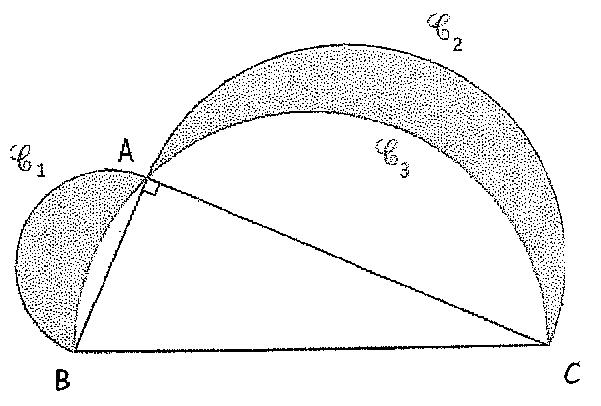
Les centres des trois demi-cercles C1,C2,C3 sont les milieux des cotés du triangle rectangle ABC. ABC est un triangle rectangle en A tel que AB= 3cm et AC= 5cm.
1)démontre que A appartient au demi-cercle C3
2)calcule l'airedes demi-cercles C1,C2,C3 puis calcule la somme des aires de C1,C2.Que remarque-t-on ?
3)démontre que la somme des deux lunules coloriées en gris, est égale à l'aire du triangle ABC.
:help: