Chaque individu de la population d'un certain pays a la probabilité p d'être atteint d'une maladie, détectable par analyse sanguine.
On veut tester un groupe de 60 personnes. Plutot que de faire 60 tests sanguins individuels, on répartit les gens en 20 groupes de 3, on mélange leurs sangs et on teste les 20 échantillons ainsi constitués.
Si le test d'un groupe est négatif, on peut écarter 3 personnes a la fois, mais s'ils est positif, il faut retester les 3 personnes concernées, séparément.
Soit X la variable aléatoire comptant le nombre de groupes dont le test est négatif
Soit T la variable aléatoire comptant le nombre de tests finalement nécessaires.
1- Quelle est la loi de probabilité X? que vaut E(X) ?
2- Démontrer que : T=80-3X. En déduire E(T).
3- Cette méthode est rentable si : E(T)<60. Démontrer que c'est le cas si : 1/3 - (1-p)au cube <0
Voila j'ai cherché le nombre d'échecs obtenus à l'issu de n tests mais je n'ai aucune idée d'une éventuelle réponse c'est pour cela que je viens demander votre aide... Merci !
Loi binomiale
8 messages
- Page 1 sur 1
charlesdu25 a écrit:toujours aucune idées !!!???
Si quelqu'un peut m'avancer en me disant la loi de probabilité de X...
Quelle est la probabilité que le test d'une personne soit négatif ?
Quelle est la probabilité que le test d'un groupe de 3 personnes soit négatif ? (noter q cette proba)
D'où la loi binomiale suivie par X ... et son espérance .... sachant qu'il y a 20 groupes.
S'il y a k tests de groupes positifs, combien de tests faudra-t-il réaliser ?
En déduire l'espérance de T...
Et vérifier que E(T) 1/3[/TEX]
Dlzlogic a écrit:Je n'ai pas d'avis sur la question, pour moi, c'est plus de l'analyse combinatoire où je suis vraiment pas entrainé.
Il y a vraiment peu d'analyse combinatoire : juste la définition de la loi binomiale.
Et tu ne penses pas que la loi normale a une rôle dans l'histoire de cet exo ? Faudrait-il en conclure que toute variable aléatoire (comme X ou T) ne suit pas forcément la loi normale ? :lol3:
Bonjour
ATTENTION !!
NE PAS CONFONDRE "analyse combinatoire" avec des calculs de nombres entiers)
nécessaires pour le calcul de la proba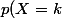) =
=)
^{n-k}) (*) pour tout entier
(*) pour tout entier 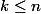
pour une v.a. X qui suit la loi Binomiale de paramètres ,
, 
(*) cette formule à apprendre "par coeur" est un grand classique (même quand on débute dans les proba)
et pour faire ces calculs il existe des calculatrices et des logiciels informatiques
ps)
Le logiciel "MS Excel" est un excellent outil pour faire ce genre de calculs
ATTENTION !!
NE PAS CONFONDRE "analyse combinatoire" avec des calculs de nombres entiers
nécessaires pour le calcul de la proba
pour une v.a. X qui suit la loi Binomiale de paramètres
(*) cette formule à apprendre "par coeur" est un grand classique (même quand on débute dans les proba)
et pour faire ces calculs il existe des calculatrices et des logiciels informatiques
ps)
Le logiciel "MS Excel" est un excellent outil pour faire ce genre de calculs
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
