Je suppose que alpha est la densité volumique de charges (et que donc dans ton énoncé tu as juste une boule chargée, sans charge surfacique supplémentaire). Il y a beaucoup d'erreurs :
1 - Une boule c'est tridimensionnel, donc le champ infinitésimal pertinent c'est celui créé par un petit volume de ta boule, autrement dit tu fais déjà fausse route quand tu n'écris qu'une intégrale de -r à r. Ta première égalité serait exacte si ton dE était le champ créé une tranche de ta distribution de charges et que le r était le rayon de la boule, mais évidemment ce dE-là a une expression qui n'est pas immédiate...
2 - On ne sait pas ce que veut dire ton r. Comme tu écris dE = k*dq/r^2, on imagine que c'est la distance entre le centre de la boule et le point où tu calcules le champ, mais dans ce cas rien ne justifie d'intégrer de -r à r, puisque r n'a rien à voir avec les propriétés de la distribution de charges.
3 - Tu écris dq = 4pi*alpha*r^2*dr donc ce coup-ci tu considères r comme une variable d'intégration, le "rayon courant" de la coquille sphérique infiniment fine que tu considères. Tu utilises donc la même lettre pour nommer 3 objets différents (rayon de la boule, variable d'intégration et distance entre le point où tu calcules le champ et le centre de la boule).
4 - Ta dernière égalité est fausse, l'intégrale de dr entre -r et r égale 2r, donc tes calculs devraient te donner 8k*pi*alpha*r (qui est faux puisque ce n'est pas le bon calcul que tu fais, mais au moins c'est homogène).
Il faut commencer par bien poser le problème. On appelle O le centre de la boule chargée, R son rayon, M le point en lequel on veut calculer le champ, qui est à une distance r de O. Comme dit, le problème est 3D et le champ électrique est un vecteur, on considère donc un petit volume d^3P centré autour d'un point P et on appelle dE le vecteur champ électrique au point M dû à d^3P. Comme d^3P peut être vu comme une charge ponctuelle de charge alpha*d^3P, on peut écrire :
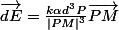
C'est donc ce truc-là que tu dois intégrer sur tous les points P de ta distribution de charge. Si tu choisis d'intégrer en coordonnées sphériques (r',theta,phi), tu tombes sur
^{3/2}}\left[(r-r'\cos\theta)\frac{\vec{OM}}{|OM|}+r'\sin\theta \cos\phi \vec{x}+r'\sin\theta\sin\phi \vec{y}\right])
où l'intégration se fait pour r' de 0 à R, theta de 0 à pi et phi de 0 à 2pi, et x et y sont deux vecteurs unitaires fixes qui forment une base orthonormée avec
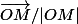
. Des arguments de parité impliquent que la contribution des termes en x et y est nulle une fois l'intégration faite, donc il te reste à calculer
^{3/2}}(r-r'\cos\theta))
ce qui n'est pas nécessairement une partie de plaisir... D'où l'utilisation du thérorème de Gauss pour se simplifier la vie.
