Bonjour, la géométrie analytique est un peu loin maintenant, et je recherche une formule qui (en deux dimensions) me donne les coordonnées de la projection d'un point sur une droite.
Les éléments à ma disposition sont les coordonnées des deux points qui définissent cette droite, ainsi que les coordonnées cartésiennes du point à projeter orthogonalement.
Merci !
Coordonnées de la projection d'un point sur une droite
10 messages
- Page 1 sur 1
avec l'équation de la droite et un produit scalaire, tu obtiens ça facilement
soit AB les points qui définissent la droite
C un point et D son projeté orthogonal sur la droite
avec les coordonnées de A et B tu connais l'équation de la droite
vecAB . vecCD = 0
avec a et b les coordonnées de D, cela te donne une autre droite
l'intersection des deux droites est le point D
on trouve ces coordonnées avec les deux équations de droites
cqfd ?
soit AB les points qui définissent la droite
C un point et D son projeté orthogonal sur la droite
avec les coordonnées de A et B tu connais l'équation de la droite
vecAB . vecCD = 0
avec a et b les coordonnées de D, cela te donne une autre droite
l'intersection des deux droites est le point D
on trouve ces coordonnées avec les deux équations de droites
cqfd ?
oui, c'est bien ce que je cherchais, mais sans passer par les produits scalaires :
soit D1 la droite sur laquelle je projette le point D(x0,y0) :
D1 : y=a.x+b
soit D2 une droite perpendiculaire à D1 :
D2 : y=(-1/a).x+c
Or D(x0,y0) appartient à cette droite D2, donc ses coordonnées vérifient l'équation de D2, soit :
D2 : y=(-1/a).x+(y0+1/a.x0)
l'intersection G de D1 et D2 est donnée en vérifiant les équations de D1 ET de D2, soit :
Gx = (x0-b+a.y0)/(1+a²)
Gy = b + a.(x0-b+a.y0)/(1+a²)
pas d'erreur ?
Merci
soit D1 la droite sur laquelle je projette le point D(x0,y0) :
D1 : y=a.x+b
soit D2 une droite perpendiculaire à D1 :
D2 : y=(-1/a).x+c
Or D(x0,y0) appartient à cette droite D2, donc ses coordonnées vérifient l'équation de D2, soit :
D2 : y=(-1/a).x+(y0+1/a.x0)
l'intersection G de D1 et D2 est donnée en vérifiant les équations de D1 ET de D2, soit :
Gx = (x0-b+a.y0)/(1+a²)
Gy = b + a.(x0-b+a.y0)/(1+a²)
pas d'erreur ?
Merci
en considérant deux points ) et
et ) qui définissent la droite
qui définissent la droite 
et un point) à projeter en
à projeter en ) sur la droite
sur la droite  :
:
j'obtiens l'équation de la droite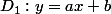
Soit la droite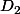 perpendiculaire à
perpendiculaire à  , elle a pour équation :
, elle a pour équation : 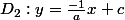
en vérifiant que les coordonnées de A et de B vérifient l'équation de on obtient :
on obtient :
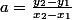
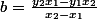
puis en vérifiant que M appartient à la droite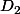 :
:
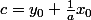
A présent je cherche l'intersection) de
de  et de
et de 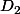 . J'obtiens
. J'obtiens  en soustrayant les équations de
en soustrayant les équations de  et de
et de 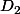 , et
, et  en les additionnant soit :
en les additionnant soit :
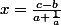
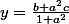
et en remplaçant a, b et c par leurs expressions données plus haut, j'obtiens :
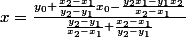
^2.(y_0+\frac{x_2-x_1}{y_2-y_1}x_0)}{1+(\frac{y_2-y_1}{x_2-x_1})^2})
ces expressions reportées dans Excel ne donnent pas les résultats escomptés.
Quelqu'un saurait-il où est mon erreur, et d'autre part aurait-il assez de malice pour factoriser tout ceci de manière plus élégante ?
Merci
et un point
j'obtiens l'équation de la droite
Soit la droite
en vérifiant que les coordonnées de A et de B vérifient l'équation de
puis en vérifiant que M appartient à la droite
A présent je cherche l'intersection
et en remplaçant a, b et c par leurs expressions données plus haut, j'obtiens :
ces expressions reportées dans Excel ne donnent pas les résultats escomptés.
Quelqu'un saurait-il où est mon erreur, et d'autre part aurait-il assez de malice pour factoriser tout ceci de manière plus élégante ?
Merci
correction
Il me semble qu'il y a une erreur dans les coordonnees de Gx et Gy dans le message de flyjodel. Ce devrait etre:
Gx = (x0-a.b+a.y0)/(1+a²)
Gy = b + a.(x0-a.b+a.y0)/(1+a²)
('b' doit etre multitplie par 'a' dans la parenthese).
En effet on doit resoudre:
y=(-1/a).x+(y0+1/a.x0)
y=a.x+b
ce qui donne:
a.x+b = (-1/a).x+(y0+1/a.x0) ==> (a+1/a).x = y0+1/a.x0-b
==> x = (y0+1/a.x0-b)/(a+1/a) = (x0-a.b+a.y0)/(1+a²) = Gx
Gx = (x0-a.b+a.y0)/(1+a²)
Gy = b + a.(x0-a.b+a.y0)/(1+a²)
('b' doit etre multitplie par 'a' dans la parenthese).
En effet on doit resoudre:
y=(-1/a).x+(y0+1/a.x0)
y=a.x+b
ce qui donne:
a.x+b = (-1/a).x+(y0+1/a.x0) ==> (a+1/a).x = y0+1/a.x0-b
==> x = (y0+1/a.x0-b)/(a+1/a) = (x0-a.b+a.y0)/(1+a²) = Gx
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
