Bonjour à tous,
imaginez un cône de révolution de 6m de diamètre et de 6m de hauteur.
Mettez la pointe du cône en bas dans votre tête, merci.
De la pointe du cône, on mesure 4m et on a à cet endroit une deuxième base.
On me demande de calculer le volume de ce cône en direction de la pointe, sachant que je n'en connais pas la dimension du rayon !
Dur , dur.
Il parait qu'il faut appliquer le théorème de Pithagore, mais il me manque des données non ?
Merci de m'aider !
Calculer le rayon d'une base d'un cône de révolution
11 messages
- Page 1 sur 1
Salut à vous, voici donc le problème exposé :
Un bassin a la forme d'un cône qui a pour base un disque de 3 m de rayon et pour hauteur 6 m.
On rempli ce bassin avec de l'eau sur une hauteur de 4 m. (Le cône sur le schéma est dessiné tête en bas).
-calculer le rayon de la base du cône d'eau ainsi formé
-en déduire, en m3, le volume d'eau présent dans le bassin
-Quelle proportion d'eau occupe le bassin ?
Voilà !
Un bassin a la forme d'un cône qui a pour base un disque de 3 m de rayon et pour hauteur 6 m.
On rempli ce bassin avec de l'eau sur une hauteur de 4 m. (Le cône sur le schéma est dessiné tête en bas).
-calculer le rayon de la base du cône d'eau ainsi formé
-en déduire, en m3, le volume d'eau présent dans le bassin
-Quelle proportion d'eau occupe le bassin ?
Voilà !
Salut,
la c'est plus clair! Bon, allons-y.
Question 1:
Il s'agit d'utiliser les triangles semblables. Les triangles sont composés de l'hypothénuse étant le bord extérieur du cône, la hauteur du triangle étant la hauteur du cône et de l'eau, et la base des triangles étants les rayons. Pour un triangle ayant une hauteur de 6m on a un rayon de 3m, donc pour un triangle ayant une hauteur de 4m on a x m de rayon.
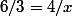
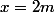
Question 2:
Le volume d'un cône est le même que celui d'une pyramide, donc:
h]/3$)
Avec r = 2m et h = 4m on a:
^2)]/3$)
/3] m^3$)
Question 3:
Une proportion n'a pas d'unité, donc c'est des m cubes sur des m cubes, tu dois d'abord trouver le volume du cône au complet.
h]/3$)
Avec r = 3m et h = 6m on a:
/3] m^3$)
Donc, on a:
/3]/[(54 \pi)/3]$) =
= 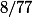
Voila, j'espere que ca t'as aidé.
la c'est plus clair! Bon, allons-y.
Question 1:
Il s'agit d'utiliser les triangles semblables. Les triangles sont composés de l'hypothénuse étant le bord extérieur du cône, la hauteur du triangle étant la hauteur du cône et de l'eau, et la base des triangles étants les rayons. Pour un triangle ayant une hauteur de 6m on a un rayon de 3m, donc pour un triangle ayant une hauteur de 4m on a x m de rayon.
Question 2:
Le volume d'un cône est le même que celui d'une pyramide, donc:
Avec r = 2m et h = 4m on a:
Question 3:
Une proportion n'a pas d'unité, donc c'est des m cubes sur des m cubes, tu dois d'abord trouver le volume du cône au complet.
Avec r = 3m et h = 6m on a:
Donc, on a:
Voila, j'espere que ca t'as aidé.
Resalut,
oui, c'est dur a représenter autrement que par un dessein, mais comme je disais tu as deux triangles.
1er triangle: le centre de la base circulaire du cône créé par l'eau jusqu'au bord du cône est la base. L'hypothénuse est du bord du cône au sommet du cône(en bas). La hauteur est du sommet du cône au centre de la base circulaire du cône créé par l'eau.
2e triangle: Même chose, sauf qu'au lieu d'utiliser le petit cône créé par l'eau, tu utilise le cône du départ(le gros).
Ensuite ben tu as deux triangles qui ont chacun des angles égaux entre eux. Ca signifie que tu peux utiliser les triangles semblables, c'est-a-dire que les côtés seront proportionnels entre eux.
tu comprends?
oui, c'est dur a représenter autrement que par un dessein, mais comme je disais tu as deux triangles.
1er triangle: le centre de la base circulaire du cône créé par l'eau jusqu'au bord du cône est la base. L'hypothénuse est du bord du cône au sommet du cône(en bas). La hauteur est du sommet du cône au centre de la base circulaire du cône créé par l'eau.
2e triangle: Même chose, sauf qu'au lieu d'utiliser le petit cône créé par l'eau, tu utilise le cône du départ(le gros).
Ensuite ben tu as deux triangles qui ont chacun des angles égaux entre eux. Ca signifie que tu peux utiliser les triangles semblables, c'est-a-dire que les côtés seront proportionnels entre eux.
tu comprends?
Calculer le rayon d'un cône de révolution
Bonjour, J'ai un DM de math et je suis bloqué sur un exercice
" Un patron d'un cône de révolution de Sommet S et dont les génératrices ont pour longueur 4.8 cm.
Calculer les valeurs arrondies au mm des longueurs :
a. de l'arc AA'
b. du rayon r de la base
c. de la hauteur
C'est un DM de 4e, il n'y a que la longueur des génératrices, aucune autre.
Merci d'avance
" Un patron d'un cône de révolution de Sommet S et dont les génératrices ont pour longueur 4.8 cm.
Calculer les valeurs arrondies au mm des longueurs :
a. de l'arc AA'
b. du rayon r de la base
c. de la hauteur
C'est un DM de 4e, il n'y a que la longueur des génératrices, aucune autre.
Merci d'avance
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
