L'inégalite sur la norme euclidienne
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Educ
- Membre Naturel
- Messages: 18
- Enregistré le: 28 Nov 2013, 17:04
-
 par Educ » 02 Déc 2013, 15:39
par Educ » 02 Déc 2013, 15:39
Bonjour,
Soit

| la norme euclidienne sur
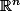
et soient

et

deux fonction continues
supposons qu' il existe une constante
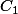
telle que :
|+|\sigma(x)| \leq C_{1}(1+|x|) \forall x \in \mathbb{R}^{n})
comment peut on montrer que ,pour
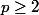
fixe , on peut trouver une constante
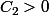
telle que :
+\frac{1}{2}p(p-1)|x|^{p-2}|\sigma(x)|^{2}\leq C_{2}(1+|x|^{p}) \forall x \in \mathbb{R}^{n})
je serais reconnaissant pour tout aide

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Déc 2013, 19:36
par Ben314 » 02 Déc 2013, 19:36
Salut,
Dés le départ, il y a un truc qui me... chagrine... : tu fait comment pour faire la somme de b(x) et de sigma(x) qui ne vivent pas dans le même espace vectoriel ?
Sinon, à la fin , je suppose que c'est un "quelque soit x dans R^n" (et pas R^d).
Et ton x.b(x), c'est le produit scalaire que tu note avec un point ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Educ
- Membre Naturel
- Messages: 18
- Enregistré le: 28 Nov 2013, 17:04
-
 par Educ » 02 Déc 2013, 21:41
par Educ » 02 Déc 2013, 21:41
Ben314 a écrit:Salut,
Dés le départ, il y a un truc qui me... chagrine... : tu fait comment pour faire la somme de b(x) et de sigma(x) qui ne vivent pas dans le même espace vectoriel ?
Sinon, à la fin , je suppose que c'est un "quelque soit x dans R^n" (et pas R^d).
Et ton x.b(x), c'est le produit scalaire que tu note avec un point ?
bonjour, merci Ben314 pour votre remarque, vous pouvez trouver ma question dans le fichier attaché page 3
source

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Déc 2013, 22:58
par Ben314 » 02 Déc 2013, 22:58
Si
|+|\sigma(x)| \leq C_{1}(1+|x|)\ \forall x \in \mathbb{R}^{n}\)
alors
+\frac{p(p-1)}{2}|x|^{p-2}|\sigma(x)|^{2})
+\frac{p(p-1)}{2}|x|^{p-2}C_{1}^2(1+|x|)^2)
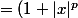\varphi(|x|))
où
+\frac{p(p-1)}{2}t^{p-2}C_{1}^2(1+t)^2}{1+t^p})
qui est bornée sur
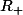
vu qu'elle y est continue et qu'elle admet une limite finie en

(le numérateur et le dénominateur sont tout les deux équivalent à
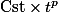
en

)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Educ
- Membre Naturel
- Messages: 18
- Enregistré le: 28 Nov 2013, 17:04
-
 par Educ » 02 Déc 2013, 23:23
par Educ » 02 Déc 2013, 23:23
Ben314 a écrit:Si
|+|\sigma(x)| \leq C_{1}(1+|x|)\ \forall x \in \mathbb{R}^{n}\)
alors
+\frac{p(p-1)}{2}|x|^{p-2}|\sigma(x)|^{2})
+\frac{p(p-1)}{2}|x|^{p-2}C_{1}^2(1+|x|)^2)
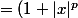\varphi(|x|))
où
+\frac{p(p-1)}{2}t^{p-2}C_{1}^2(1+t)^2}{1+t^p})
qui est bornée sur
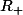
vu qu'elle y est continue et qu'elle admet une limite finie en

(le numérateur et le dénominateur sont tout les deux équivalent à
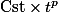
en

)
Merci Ben314 mais j'ai pas saisie les dernière lignes de votre raisonnement s'il vous plait dis moi est ce que cette inégalité suivante juste :
^{p}\leq 2^{p-1}(1+|x|^{p}) \forall p\geq 2)
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 06 Déc 2013, 14:41
par deltab » 06 Déc 2013, 14:41
Bonjour
Educ a écrit:bonjour, merci Ben314 pour votre remarque, vous pouvez trouver ma question dans le fichier attaché page 3
source
Ta source est inexistante dans le lien donné. Elle nous renvoie vers un autre site (publicité)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
alors
vu qu'elle y est continue et qu'elle admet une limite finie en
(le numérateur et le dénominateur sont tout les deux équivalent à
en
)