Bonjour en fait je bloque sur un truc probablement tout bête dont j'aurais besoin pour un programme.
Donc voilà:
Si je peu tirer n fois a répétition un nombre entre 1 et 4.
Comment calculer le pourcentage de chance d'être tomber sur tous les chiffres?
en vous remerciant d'avance.
Petit problème de probabilité
6 messages
- Page 1 sur 1
Une façon de voir le problème (sous la forme d'une "chaîne de Markov"), c'est de noter  les proba. respective d'avoir tiré exactement 1,2,3 ou 4 nombres différents après n tirages.
les proba. respective d'avoir tiré exactement 1,2,3 ou 4 nombres différents après n tirages.
Si on pose) alors
alors ) et
et  où
où ) (matrice dite "de transition")
(matrice dite "de transition")
et... y'a "plus qu'à" calculer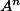
Si on pose
et... y'a "plus qu'à" calculer
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
En fait, si c'est le résultat qui t'interesse, au vu des valeurs propres de A, on sait d'avance que
^n+\gamma(1/2)^n+\delta(1/4)^n) où
où 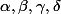 sont des constantes.
sont des constantes.
Deux sous de bon sens montrent que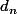 tend vers 1 lorsque n tend vers l'infini donc
tend vers 1 lorsque n tend vers l'infini donc 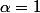
Et on trouve (assez) facilement les 3 autres en écrivant que :
:
^n+6(1/2)^n-4(1/4)^n)
Deux sous de bon sens montrent que
Et on trouve (assez) facilement les 3 autres en écrivant que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
salut
Une autre approche
On peut considérer que l'expérience consiste à remplir un tableau à n colonnes et 4 lignes en mettant une et une seule croix par colonne.

On cherche la probabilité pour qu'aucune ligne ne soit vide.
nombre de possibilités=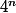
nombre de façons avec exactement 3 lignes vides = 4
nombre de façons avec exactement 2 lignes vides:)
(on multiplie par 6 car on choisit 2 lignes parmi 4 et on enlève 2 à pour ne pas avoir 3 lignes vides)
pour ne pas avoir 3 lignes vides)
nombre de façons avec exactement 1 ligne vide (même méthode)
))
nombre de façons avec au moins une ligne vide:
+4(3^n -3-3(2^n -2))=4+6\times 2^n -12+4\times 3^n -12-12\times 2^n+24)
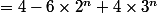
la proba demandée est
soit^n +6(\fra{1}{2})^n -4(\fra{3}{4})^n)
Ci-dessous les premières valeurs

on a bien 0 pour n<4
pour n=4, on a bien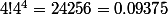
Une autre approche
On peut considérer que l'expérience consiste à remplir un tableau à n colonnes et 4 lignes en mettant une et une seule croix par colonne.

On cherche la probabilité pour qu'aucune ligne ne soit vide.
nombre de possibilités=
nombre de façons avec exactement 3 lignes vides = 4
nombre de façons avec exactement 2 lignes vides:
(on multiplie par 6 car on choisit 2 lignes parmi 4 et on enlève 2 à
nombre de façons avec exactement 1 ligne vide (même méthode)
nombre de façons avec au moins une ligne vide:
la proba demandée est
soit
Ci-dessous les premières valeurs

on a bien 0 pour n<4
pour n=4, on a bien
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
