Devoir maison de maths pour la rentrée

[mcar0nd]

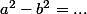
Salut, alors pour l'équation , regroupe tout d'un même côté et factorise avec l'identité remarquable . Tu trouves quoi?

[mcar0nd]

Bonjour, donc si je regroupe tous d'un même côté avec l'identité remarquable ça fais donc :
2x²-2*2x*(-3)+(-3)²=49
2x²+12x+9=49
2x²+12x+9-49=0
2x²+12x-40=0

Non , c'est pas ça j'ai vraiment du mal.

Non, en fait, ce que je voulais te dire, c'est d'écrire ton équation comme étant soit .
Maintenant, tu vois que ton membre de gauche est de la forme , donc tu peux factoriser à l'aide d'une identité remarquable.

[Carpate]

Donc cette identité remarquable c'est: a²-b²= (a-b)(a+b)
: (2x-3-7)(2x-3+(-7))=0
2x-10)(2x-10)=0
:4x-20=0
:4x-20+20=0+20
: 4x=20
: 4x/4=20/4
=5

Non, applique la formule avec
a=2x-3
b=7

[mcar0nd]

Bonjour, donc a²-b²
c'est= 2x-3²-7²
(2x-3-7)(2x-3+7)=0
C'est ça?

Oui, c'est ça, et tu peux simplifier un peu l'écriture pour te retrouver avec , que tu peux résoudre maintenant.

[mcar0nd]

Merci , donc ça fait (2x-3-7)(2x-3+7)=0
(2x-10)(2x+4)=0
4x-40=0
4x-40+40=0+40
4x/4=40/4
x=10

Pourquoi 4x-40=0?
Un produit est nul si l'un au moins des termes est nuls dont 2x-10=0 ou 2x+4=0.

[mcar0nd]

A oui programme de 3 ème ! Donc sa fait : 2x-10=0
: 2x-10=0+10
: 2x/2=10/2
x=5
2x+4=0
2x+4=0-4
2x=-4/2
x=-2
Donc l'équation compte 2 solutions x=5ou x=-2

Je pense que c'est enfin ça

Oui c'est bien ça.

Donc, on passe à l'ex 2.
La question 1 est facile.
Pour la deuxième, tu dois résoudre . Le membre de gauche ne te fait pas penser à une identité remarquable?

[mcar0nd]

Merci beaucoup ! Pour la 2 j'ai fait f(x)=1 donc; -x²+2x=1
x²-2x+1=0
(x-1)²=0
x=1
Un antécédents de 1 par la fonction f est 1.

Oui, c'est tout juste ça.
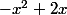
Pour la question c), tu développe juste l'expression qu'on te donneur retrouver . Et ensuite tu résous .

[mcar0nd]

Donc -(x-1)²+1=-(x²-2x+1)+1
= -x²+2x-1+1
=-x²+2x
Donc f(x)=-(x-1)²


si 2 à un ou pplusieur antécédents alors -(x-1)²+1=2 et (x-1)²=-1, ce qui n'est pas possible car un carré ne peut pas être négative, donc on peux conclure que 2 n'as pas d'antécédents.

C'est encore tout juste ça.

La question 2a) est facile. Pour la question 2.b), est ce que tu as réussi?

[mcar0nd]

Pour la 2)b , je pense que c'est bon mais dans la 2)a quand il me demande d'émettre une conjecture sur le sens de variation f , je n'est pas très bien compris ce que cela signifie

Pour la 2.a), il faut que tu conjecture, que tu émette une hypothèse sur le(s) sens de variation(s) de la fonction f: semble-t-elle croissante? décroissante? constante?