Limite
24 messages
- Page 2 sur 2 - 1, 2
par fonfon » 04 Sep 2006, 19:26
Re, les limites citées par nekros plu haut sont à savoir en terminale pour t'en sortir car sinon il y a bien d'autres methodes mais ca ne se fait pas au lycée,sinon utiliser le taux d'accroissement
par nekros » 04 Sep 2006, 19:27
Re,
Pour les limites connues :
Par exemple, pour la limite de}{x})
en 
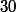
, tu peux utiliser le taux d'accroissement.
Tu poses=ln(1+x))
donc =0)
Tu remarques donc que}{x}=\frac{f(x)-f(0)}{x-0} -> f'(0)=1)
quand 
tend vers
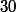
A+
Pour les limites connues :
Par exemple, pour la limite de
Tu poses
Tu remarques donc que
A+
par fonfon » 04 Sep 2006, 19:40
je peux te demontrer que lim ln(x)/x=0+ qd x->+inf
donc
}=\int_{1}^{x}\frac{1}{t}\ dt)
pour t>1,
on a:
}>[2\sqrt{t}]_{1}^{x})
donc
<2\sqrt{x}-2<2\sqrt{x})
donc
}{x}<\frac{2\sqrt{x}}{x})
et en passant à la limite et th. des gendarmes on a la resultat
donc
pour t>1,
on a:
donc
donc
et en passant à la limite et th. des gendarmes on a la resultat
par nekros » 04 Sep 2006, 19:45
Bien vu fonfon,
j'allais justement écrire qu'on pouvait déterminer cette limite en étudiant la fonction
définie par =ln(x)-2\sqrt x)
Mais c'est beaucoup plus long...
A+
j'allais justement écrire qu'on pouvait déterminer cette limite en étudiant la fonction
Mais c'est beaucoup plus long...
A+
24 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :