Simplification d'une Somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 26 Sep 2013, 22:19
par Gonra » 26 Sep 2013, 22:19
Bonsoir,
j'aurais besoin d'aide pour factoriser ces termes :
1+x+x²+x^3+5x^4+4x^5+4x^6+4x^7+4x^8+5x^9
ma methode :
1+x+x²+x^3+5(x^4+x^9)+4(x^5+x^6+x^7+x^8)
si quelqun peut me donner une piste ..
merci d'avance
j'ai pensé à utiliser les sigma puis la somme géométrique mais le simplifie pas trop..

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 26 Sep 2013, 22:21
par fatal_error » 26 Sep 2013, 22:21
en tout cas, il semblerait que -1 soit solution
la vie est une fête

-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 26 Sep 2013, 22:25
par Gonra » 26 Sep 2013, 22:25
il n'y a pas de résolution à faire , je dois juste essayer de factoriser pour calculer ces termes avec x=exp((2*pi*i)/5)
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 26 Sep 2013, 22:31
par Gonra » 26 Sep 2013, 22:31
1+x+x²+x^3+5(x^4+x^9)+4(x^5+x^6+x^7+x^8)
1+x+x²+x^3+5(x^4+x^9)+4x^4(1+x^2+x^3+x^4)
(1+x^2+x^3+x^4)(1+4x^4)+5(x^4+x^9)
je bloque ici .. si j'utilise sigma je complique la chose , il n'y a pas d'autres solutions ?
-
EulBofo
- Messages: 4
- Enregistré le: 26 Sep 2013, 23:14
-
 par EulBofo » 26 Sep 2013, 23:20
par EulBofo » 26 Sep 2013, 23:20
Factoriser, là, tout de suite, je n'ai pas d'idée (et MuPAD non plus, d'ailleurs !). Par contre, s'il s'agit de calculer l'expression en
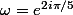
, on peut faire ça :
=(1+x+x^2+x^3+x^4)(1+4x^4)+5x^9)
L'intérêt est que le terme

s'annule en

.
On trouve donc
=5\omega^9=\frac{5}{\omega})
J'ai pas mieux.
\bye
-
Gonra
- Membre Relatif
- Messages: 100
- Enregistré le: 06 Déc 2012, 21:34
-
 par Gonra » 27 Sep 2013, 00:04
par Gonra » 27 Sep 2013, 00:04
Merci pour votre aide je n'y avait pas pensée
Bonne soirée nuit ;) je trouve bien le bon résultat au final
-
LA solution
- Membre Relatif
- Messages: 165
- Enregistré le: 28 Déc 2012, 17:11
-
 par LA solution » 27 Sep 2013, 01:51
par LA solution » 27 Sep 2013, 01:51
=1+x+x^2+x^3+x^4+x^5+x^6+x^7+x^8+x^9=(\frac{1-x^{10}}{1-x}))
h
-
LA solution
- Membre Relatif
- Messages: 165
- Enregistré le: 28 Déc 2012, 17:11
-
 par LA solution » 27 Sep 2013, 02:21
par LA solution » 27 Sep 2013, 02:21
LA solution a écrit:=1+x+x^2+x^3+x^4+x^5+x^6+x^7+x^8+x^9=(\frac{1-x^{10}}{1-x}))
h
ne le prends en pas compte j ai tou melange

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 27 Sep 2013, 08:57
par chan79 » 27 Sep 2013, 08:57
LA solution a écrit:ne le prends en pas compte j ai tou melange
salut
si on cherche la valeur pour 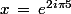
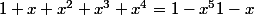
si x est égal à

, alors
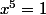
on a donc dans ce cas
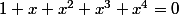
on voit alors que l'expression vaut
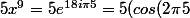-i\ sin(\fra{2\pi}{5})))
soit:

sinon, comme l'a dit fatal_error, -1 est une racine, ce qui donne
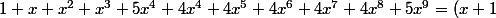(5x^8-x^7+5x^6-x^5+5x^4+x^2+1))
edit: grillé, je viens de voir que EulBofo a proposé la même chose :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
