Trigonometrie
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
vincepi
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Juil 2013, 14:38
-
 par vincepi » 15 Juil 2013, 15:17
par vincepi » 15 Juil 2013, 15:17
bonjour, toujours dans ma trigo je coince sur une equation:
sinx+4-sqrt{3}=0)
[/TEX]
j'ai bien compris que je devai remplacer cos² par 1-sin²pour obtenir une simple equation du second degrés mais j' over dose de trigo et je suis plus sur de rien
vivement que j'ai fini ces exams.

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 15 Juil 2013, 15:21
par ampholyte » 15 Juil 2013, 15:21
Bonjour,
Comme tu l'as parfaitement dit il suffit de remplacer cos²(x) par 1 - sin²(x).
Il te suffit ensuite de poser X = sin(x) et résoudre l'équation du second degré.
-
vincepi
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Juil 2013, 14:38
-
 par vincepi » 15 Juil 2013, 15:24
par vincepi » 15 Juil 2013, 15:24
merci,
je m'y remet alors
-
vincepi
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Juil 2013, 14:38
-
 par vincepi » 15 Juil 2013, 15:53
par vincepi » 15 Juil 2013, 15:53
le discriminant serait il

?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 15 Juil 2013, 15:56
par Shew » 15 Juil 2013, 15:56
ampholyte a écrit:Bonjour,
Comme tu l'as parfaitement dit il suffit de remplacer cos²(x) par 1 - sin²(x).
Il te suffit ensuite de poser X = sin(x) et résoudre l'équation du second degré.
Je ne pense pas qu'il soit necessaire de poser X , je veux dire que le résultat est assez significatif pour en venir directement à une conclusion
vincepi a écrit:le discriminant serait il

?
Pas besoin de discriminant dans ce cas précis , une fois que vous avez reussi à simplifier la première partie , vous pouvez directement factoriser le tout .

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 15 Juil 2013, 16:05
par ampholyte » 15 Juil 2013, 16:05
Shew a écrit:Je ne pense pas qu'il soit necessaire de poser X , je veux dire que le résultat est assez significatif pour en venir directement à une conclusion
Tu as parfaitement raison, je n'ai pas essayé de le résoudre. Mais c'est vrai que vu la forme il est beaucoup plus simple de passer par une factorisation !
-
vincepi
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Juil 2013, 14:38
-
 par vincepi » 15 Juil 2013, 16:10
par vincepi » 15 Juil 2013, 16:10
ampholyte a écrit:Tu as parfaitement raison, je n'ai pas essayé de le résoudre. Mais c'est vrai que vu la forme il est beaucoup plus simple de passer par une factorisation !
ah?? ok
je recommence alors
-
vincepi
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Juil 2013, 14:38
-
 par vincepi » 15 Juil 2013, 16:23
par vincepi » 15 Juil 2013, 16:23
ok pauuuuuse
à plus merci je m'y remet dans 10 min

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 15 Juil 2013, 20:55
par capitaine nuggets » 15 Juil 2013, 20:55
Salut !
\ :\quad -4\cos^2 (x) +2\(\sqrt 3 -1\)\sin(x) +4-\sqrt 3 = 0)
1°/ Montre en utilisant le fait que
=1-\sin^2(x))
que ton équation équivaut à :
 +2\(\sqrt 3 -1\)\sin(x) -\sqrt 3 = 0)
2°/ Posons alors
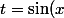)
.
Montre que le discriminant du trinôme associé

vaut
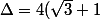^2)
.
3°/ Résous alors
t -\sqrt 3 = 0)
puis déduis-en les solutions de l'équation :
 +2\(\sqrt 3 -1\)\sin(x) -\sqrt 3 = 0)
C'es-à-dire, les solutions de
)
.
:+++:
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 15 Juil 2013, 21:38
par Shew » 15 Juil 2013, 21:38
capitaine nuggets a écrit:Salut !
\ :\quad -4\cos^2 (x) +2\(\sqrt 3 -1\)\sin(x) +4-\sqrt 3 = 0)
1°/ Montre en utilisant le fait que
=1-\sin^2(x))
que ton équation équivaut à :
 +2\(\sqrt 3 -1\)\sin(x) -\sqrt 3 = 0)
2°/ Posons alors
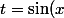)
.
Montre que le discriminant du trinôme associé

vaut
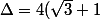^2)
.
3°/ Résous alors
t -\sqrt 3 = 0)
puis déduis-en les solutions de l'équation :
 +2\(\sqrt 3 -1\)\sin(x) -\sqrt 3 = 0)
C'es-à-dire, les solutions de
)
.
:+++:
Cela me semble plutôt long , il y'a plus évident mais c'est mon avis :lol3:

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 15 Juil 2013, 21:47
par capitaine nuggets » 15 Juil 2013, 21:47
Shew a écrit:Cela me semble plutôt long , il y'a plus évident mais c'est mon avis :lol3:
Oui, je suis d'accord.
Toutefois, on est parti de cette idée de résoudre l'équation avec un changement de variable pour se ramener à une équation du second degré donc, j'ai donné une méthode.
:++:
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 15 Juil 2013, 22:01
par Shew » 15 Juil 2013, 22:01
capitaine nuggets a écrit:Oui, je suis d'accord.
Toutefois, on est parti de cette idée de résoudre l'équation avec un changement de variable pour se ramener à une équation du second degré donc, j'ai donné une méthode.
:++:
D'accord , je comprends

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 16 Juil 2013, 05:32
par capitaine nuggets » 16 Juil 2013, 05:32
Shew a écrit:D'accord , je comprends
Pas de soucis :lol3:
Tiens, je viens de voir que, finalement, mon autre méthode tombe à l'eau (erreur de calcul

)
Du coup, comment aurais-tu traité cet résolution plus simplement ?
-
vincepi
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Juil 2013, 14:38
-
 par vincepi » 16 Juil 2013, 14:45
par vincepi » 16 Juil 2013, 14:45
capitaine nuggets a écrit:Pas de soucis :lol3:
Tiens, je viens de voir que, finalement, mon autre méthode tombe à l'eau (erreur de calcul

)
Du coup, comment aurais-tu traité cet résolution plus simplement ?
moi je trouve:
sinx-sqrt{3}=0)
pour trouver delta
^2)
c'est toujours faux?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 16 Juil 2013, 15:34
par Shew » 16 Juil 2013, 15:34
vincepi a écrit:moi je trouve:
sinx-sqrt{3}=0)
pour trouver delta
^2)
c'est toujours faux?
Si vous voulez trouver delta , rappelez vous que
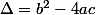
. Neanmoins vous devriez d'abord continuer à développer cette expression :
sinx-sqrt{3}=0)
-
vincepi
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Juil 2013, 14:38
-
 par vincepi » 16 Juil 2013, 15:41
par vincepi » 16 Juil 2013, 15:41
Shew a écrit:Si vous voulez trouver delta , rappelez vous que
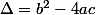
. Neanmoins vous devriez d'abord continuer à développer cette expression :
sinx-sqrt{3}=0)
J'ai remplacé sin x par X
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 16 Juil 2013, 15:45
par Shew » 16 Juil 2013, 15:45
vincepi a écrit:J'ai remplacé sin x par X
Je ne pense pas que ce soit necessaire mais supposons , vous avez désormais cette équation :
X - \sqrt{3})
, développez
X)
-
vincepi
- Membre Naturel
- Messages: 15
- Enregistré le: 04 Juil 2013, 14:38
-
 par vincepi » 25 Juil 2013, 16:30
par vincepi » 25 Juil 2013, 16:30
Shew a écrit:Je ne pense pas que ce soit necessaire mais supposons , vous avez désormais cette équation :
X - \sqrt{3})
, développez
X)
bonjour me revoila avec un peu de retard
j'en etait doncà
X-sqrt{3}=0)
^2-4*4*(-sqrt{3}))
+16sqrt{3})
...

)
...
^2)
jusque la je suis bon ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 103 invités
?
que ton équation équivaut à :
.
vaut
.
puis déduis-en les solutions de l'équation :
.