Convergence d'une série avec paramètre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Beamer1000
- Messages: 8
- Enregistré le: 16 Mai 2013, 19:23
-
 par Beamer1000 » 17 Mai 2013, 10:48
par Beamer1000 » 17 Mai 2013, 10:48
Bonjour,
C'est la premiere fois que je post ici et j'ai une question sur une preuve qui parait louche:
On cherche les
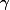
tel que
=\sum_{k=-\dfrac{N}{2}..\dfrac{N}{2},k\neq a,b}\left(\dfrac{| a-b|^\gamma}{| a-k|^\gamma| k-b|^\gamma}\right)$)
converge avec

et ce
\in \left[\dfrac{-N}{2},\dfrac{N}{2}\right]$)
.
Je symmetrise mon problème (en choisisant arbitrairement l'origine) de tel sorte que

et

En séparant ma somme en deux j'obtiens:
=\sum_{|k|>\dfrac{\lambda}{2}}\left(\dfrac{| \lambda|^\gamma}{| \dfrac{\lambda}{2}-k|^\gamma| k+\dfrac{\lambda}{2}|^\gamma}\right)+\sum_{|k|1/2$)
.
Je peux aussi majorer ma première somme par cette somme:
$)
Mais maintenant si je prend

avec

!
Mon probleme est de savoir si c'est bien légale (j'aimerai des arguments claire pour ou contre) si c'est normale quand on prend

qui croit à peut près comme N de trouver un critère different (et si c'est bien légale).
Merci de votre aide.
David
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 17 Mai 2013, 13:25
par arnaud32 » 17 Mai 2013, 13:25
tu peux tout simplement constater que il existe k0 tel que pour k > k0,
|k-a|> (k*|b-a|)^1/2 et |k-b|> (k*|b-a|)^1/2
-
Beamer1000
- Messages: 8
- Enregistré le: 16 Mai 2013, 19:23
-
 par Beamer1000 » 17 Mai 2013, 14:55
par Beamer1000 » 17 Mai 2013, 14:55
arnaud32 a écrit:tu peux tout simplement constater que il existe k0 tel que pour k > k0,
|k-a|> 2*|b-a|^1/2 et |k-b|> 2*|b-a|^1/2
Hum j'ai du mal à voir où tu veux en venir:
Tu veux dire qu'a partir d'un k0 la suite sera majoré par

??
Sauf que cela diverge.
Où alors j'ai pas compris ce que tu voulais dire.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 17 Mai 2013, 15:08
par arnaud32 » 17 Mai 2013, 15:08
pardon j'ai mal tape ma formule, je te l'ai corrigee dans le post precedent
en fait le terme general de ta 'serie' est equivalent

tout simplment
-
Beamer1000
- Messages: 8
- Enregistré le: 16 Mai 2013, 19:23
-
 par Beamer1000 » 17 Mai 2013, 15:30
par Beamer1000 » 17 Mai 2013, 15:30
Donc que cette série converge seulemement pour

.
D'accord mais pour

qui tend vers l'infini? Ou plus précisement qui croit comme la taille de l'intervalle? (en cN^\mu où \mu<1)
A t'on toujours le même critère?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 17 Mai 2013, 15:33
par arnaud32 » 17 Mai 2013, 15:33
a priori tu fixes a et b
-
Beamer1000
- Messages: 8
- Enregistré le: 16 Mai 2013, 19:23
-
 par Beamer1000 » 17 Mai 2013, 15:43
par Beamer1000 » 17 Mai 2013, 15:43
Hum c'est de ça dont je suis pas sur, ya pa moyen de prendre la limite quand |a-b|->l'infini ?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 17 Mai 2013, 15:45
par arnaud32 » 17 Mai 2013, 15:45
tu veux definir T(a,b) en faisant bouger a et b? c'est quoi ta definition d'un fonction?
-
Beamer1000
- Messages: 8
- Enregistré le: 16 Mai 2013, 19:23
-
 par Beamer1000 » 17 Mai 2013, 15:53
par Beamer1000 » 17 Mai 2013, 15:53
J'ai le droit de prendre la limite b=0 et a->infini sur ma fonction non?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 17 Mai 2013, 15:54
par arnaud32 » 17 Mai 2013, 15:54
avant de prendre une limite de fonction faut deja prouver que ta fonction existe et est bien definie
-
Beamer1000
- Messages: 8
- Enregistré le: 16 Mai 2013, 19:23
-
 par Beamer1000 » 17 Mai 2013, 18:03
par Beamer1000 » 17 Mai 2013, 18:03
Justement est ce que le fait de faire comme j'ai dit est une preuve que la limite existe seulement pour gamma>1?
-
Beamer1000
- Messages: 8
- Enregistré le: 16 Mai 2013, 19:23
-
 par Beamer1000 » 22 Mai 2013, 14:28
par Beamer1000 » 22 Mai 2013, 14:28
Quelq'un serait t'il comment justifier l'existence et calculer la limite pour par exemple T(0,b) avec b qui tend vers l'infini?
-
Beamer1000
- Messages: 8
- Enregistré le: 16 Mai 2013, 19:23
-
 par Beamer1000 » 02 Juin 2013, 19:17
par Beamer1000 » 02 Juin 2013, 19:17
Bonjour,
Je me permet de poser une question similaire et peut-être plus claire:
J'ai cette somme:
^\alpha n^\alpha}\right))
j entier naturel et 11/2[/TEX] quelque soit j.
Mais maintenant je voudrais montrer (je suis quasiment sûr que c'est vrai) que pour

, la serie (ou la somme avec L qui tend vers l'infini) diverge quand j tend vers l'infini.
Je sais déjà que la série est croissante avec j mais je n'arrive pas à montrer quelle est non bornée.
Ou bien autre piste serait de prendre la limite j tend vers l'infini dans la série et avoir un serie de terme général 1/n donc divergente. Mais pour faire ça il faut des justifications.
Pouvez vous m'aider?
Merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
