Calcul de limite d'une forme indéterminée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
HERCOLUBUS
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Nov 2011, 22:43
-
 par HERCOLUBUS » 25 Sep 2012, 22:14
par HERCOLUBUS » 25 Sep 2012, 22:14
Soit la limite suivante :
lim

x->0
Je dois identifier la forme indéterminée initiale puis évaluer la limite !
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 25 Sep 2012, 22:44
par Judoboy » 25 Sep 2012, 22:44
Tu connais les développements limité usuels ?
-
Alannaria
- Membre Relatif
- Messages: 100
- Enregistré le: 27 Sep 2012, 08:20
-
 par Alannaria » 27 Sep 2012, 08:54
par Alannaria » 27 Sep 2012, 08:54
HERCOLUBUS a écrit:Soit la limite suivante :
lim

x->0
Je dois identifier la forme indéterminée initiale puis évaluer la limite !
Applique les DL usuels de sin x et tan x puis simplifie cette fraction rationnelle (l'ordre 2 en x^3 suffit).
-
fm31
- Membre Relatif
- Messages: 145
- Enregistré le: 21 Avr 2012, 16:32
-
 par fm31 » 27 Sep 2012, 14:17
par fm31 » 27 Sep 2012, 14:17
Bonjour ,
tu peux aussi diviser numérateur et dénominateur par x ce qui donne (1 - ((sin x) / x)) / (((tg x) / x) - 1)
-
HERCOLUBUS
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Nov 2011, 22:43
-
 par HERCOLUBUS » 16 Oct 2012, 21:12
par HERCOLUBUS » 16 Oct 2012, 21:12
HERCOLUBUS a écrit:Soit la limite suivante :
lim

x->0
Je dois identifier la forme indéterminée initiale puis évaluer la limite !
D'abord, je crois que c'est une forme indéterminée
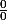
Donc j'applique la règle de l'Hospital, ce qui me donne :-

c'est une forme indéterminée
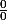
Donc j'applique la règle de l'Hospital à nouveau... ???
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 16 Oct 2012, 21:45
par ThekamikazeFou » 16 Oct 2012, 21:45
HERCOLUBUS a écrit:D'abord, je crois que c'est une forme indéterminée
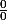
Donc j'applique la règle de l'Hospital, ce qui me donne :-

c'est une forme indéterminée
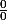
Donc j'applique la règle de l'Hospital à nouveau... ???
Tu connais la limite de (cosx-1)/x non? Et de x/ tan x^2 aussi a mon avis .
-
HERCOLUBUS
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Nov 2011, 22:43
-
 par HERCOLUBUS » 16 Oct 2012, 22:09
par HERCOLUBUS » 16 Oct 2012, 22:09
ThekamikazeFou a écrit:Tu connais la limite de (cosx-1)/x non? Et de x/ tan x^2 aussi a mon avis .
:hein: k?
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 16 Oct 2012, 22:14
par ThekamikazeFou » 16 Oct 2012, 22:14
-

=
-

Or lim x->0 de

= 1
Et lim x->0 de

= 1
Donc ton fonction tend vers -1/x en 0
-
HERCOLUBUS
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Nov 2011, 22:43
-
 par HERCOLUBUS » 16 Oct 2012, 23:04
par HERCOLUBUS » 16 Oct 2012, 23:04
ThekamikazeFou a écrit:-

=
-

Or lim x->0 de

= 1
Et lim x->0 de

= 1
Donc ton fonction tend vers -1/x en 0
lim -
-1}{tan(x)^2})
quand x tend vers 0 =
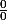
Donc il faut appliquer la règle de l'Hospital à nouveau je crois.
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 16 Oct 2012, 23:10
par ThekamikazeFou » 16 Oct 2012, 23:10
HERCOLUBUS a écrit:lim -
-1}{tan(x)^2})
quand x tend vers 0 =
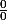
Donc il faut appliquer la règle de l'Hospital à nouveau je crois.
Je viens de te prouver le contraire! ..
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 17 Oct 2012, 09:11
par Carpate » 17 Oct 2012, 09:11
ThekamikazeFou a écrit:Je viens de te prouver le contraire! ..
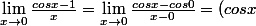'_{0}= -sin0=0)
On applique une deuxième fois la règle de l'Hospital et on trouve
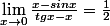
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 17 Oct 2012, 11:56
par ThekamikazeFou » 17 Oct 2012, 11:56
Carpate a écrit: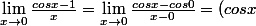'_{0}= -sin0=0)
On applique une deuxième fois la règle de l'Hospital et on trouve
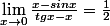
Effectivement je me suis trompé j'avais souvenir que la limite etait 1...
-
Black Jack
 par Black Jack » 17 Oct 2012, 13:24
par Black Jack » 17 Oct 2012, 13:24
HERCOLUBUS a écrit:D'abord, je crois que c'est une forme indéterminée
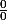
Donc j'applique la règle de l'Hospital, ce qui me donne :-

c'est une forme indéterminée
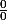
Donc j'applique la règle de l'Hospital à nouveau... ???
Contrairement à ce que y a été dit, ... oui bien sûr.
************
lim(x--> 0) [(x-sin(x))/(tan(x)-x)] est de la forme 0/0 --> application de la règle de Lhospital.
= lim(x--> 0) [(1-cos(x))/(1/cos²(x) - 1)]
= lim(x--> 0) [(1-cos(x))/tan²(x)] est de la forme 0/0 --> application de la règle de Lhospital.
= lim(x--> 0) [sin(x)/(2.tan(x)/cos²(x))] = lim(x--> 0) [cos³(x)/2] = 1/2
:zen:
-
HERCOLUBUS
- Membre Relatif
- Messages: 105
- Enregistré le: 15 Nov 2011, 22:43
-
 par HERCOLUBUS » 18 Oct 2012, 01:46
par HERCOLUBUS » 18 Oct 2012, 01:46
Black Jack a écrit:Contrairement à ce que y a été dit, ... oui bien sûr.
************
lim(x--> 0) [(x-sin(x))/(tan(x)-x)] est de la forme 0/0 --> application de la règle de Lhospital.
= lim(x--> 0) [(1-cos(x))/(1/cos²(x) - 1)]
= lim(x--> 0) [(1-cos(x))/tan²(x)] est de la forme 0/0 --> application de la règle de Lhospital.
= lim(x--> 0) [sin(x)/(2.tan(x)/cos²(x))] = lim(x--> 0) [cos³(x)/2] = 1/2
:zen:
Merci à tous ! :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités

