Méca quantique (whooaaa ;D)

[globule rouge]

Bonsoir :)

Ce matin, j'ai essayé une olympiade de physique avec mon prof. C'est celle de 97.
Alors la deuxième question est :

" b) The radius of a hydrogen atom in its ground state is a0 = 0.0529 nm (the “Bohr radius”). What is the radius a' of a “muonic-hydrogen” atom in which the electron is replaced by an identically charged muon, with mass 207 times that of the electron? Assume the proton mass is much larger than that of the muon and electron. (2 marks)"

Trad : "Le rayon d'un atome d'hydrogène en son état fondamental vaut a0 = 0,0529 nm (le "rayon de Bohr").
Quel est le rayon a' d'un atome d' "hydrogène muonique", dont l'électron a été remplacé par un muon de charge identique et dont la masse est 207 fois supérieure ?
Considérez que les masses du muon et de l'électron sont négligeables face à celle du proton."


Bon, j'avais commencé par calculer la force électrique reliant le proton et le muon et j'en suis restée là. ^^ Mon prof m'a proposé une résolution énergétique nécessitant des outils supérieurs au niveau terminale (mq) donc je voulais vous demander si vous auriez pas une résolution employant des notions de Terminale seulement !

Enfin vu la tête de la solution, je pense que ça doit pas être trop dur à comprendre finalement. Cela s'inspire de la méca classique céleste, non ?

Merci :)

Julie

[Mathusalem]

Bonsoir

Ce matin, j'ai essayé une olympiade de physique avec mon prof. C'est celle de 97.
Alors la deuxième question est :

" b) The radius of a hydrogen atom in its ground state is a0 = 0.0529 nm (the “Bohr radius”). What is the radius a' of a “muonic-hydrogen” atom in which the electron is replaced by an identically charged muon, with mass 207 times that of the electron? Assume the proton mass is much larger than that of the muon and electron. (2 marks)"

Trad : "Le rayon d'un atome d'hydrogène en son état fondamental vaut a0 = 0,0529 nm (le "rayon de Bohr").
Quel est le rayon a' d'un atome d' "hydrogène muonique", dont l'électron a été remplacé par un muon de charge identique et dont la masse est 207 fois supérieure ?
Considérez que les masses du muon et de l'électron sont négligeables face à celle du proton."


Bon, j'avais commencé par calculer la force électrique reliant le proton et le muon et j'en suis restée là. ^^ Mon prof m'a proposé une résolution énergétique nécessitant des outils supérieurs au niveau terminale (mq) donc je voulais vous demander si vous auriez pas une résolution employant des notions de Terminale seulement !

Enfin vu la tête de la solution, je pense que ça doit pas être trop dur à comprendre finalement. Cela s'inspire de la méca classique céleste, non ?

Merci

Julie

Mais t'as le droit d'utiliser quoi comme outils, et t'es supposée connaître quoi ?

Car me mettant dans ta position, si je sais que ça contient du quantique, donc la constante de planck, j'attaque l'analyse dimensionnelle tout de suite pour voir que le-dit rayon dépend inversément de la masse.

[Mathusalem]

Peut-être que c'est pas trop clair comment attaquer l'analyse dimensionnelle, m'enfin voilà :

On a un problème avec un proton, un électron, qui intéragissent via la force électrostatique. On sait aussi que l'on doit résonner dans le domaine quantique (dominé par ).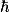

Pour déterminer le jeu de dimensions qui nous intéresse, prenons les relations suivantes :




Puis on a un électron de masse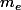 et un proton de passe 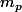. Cependant, ainsi le résultat final ne dépend pas de la masse du proton.

On s'intéresse au rayon de bohr, donc à une distance.

Ainsi,


grâce aux relations plus haut, on sait que . On remarque également que ce qui est vachement bien parce qu'on va pouvoir s'arranger pour tuer du Newton et en même temps on vire une dimension (le Coulomb se voit disparaître dans la contraction ke^2)

On tente de remplacer dans la relation plus haut . Y a d'autres manières de raisonner mais ça c'est bien.

. Pour rendre un peu plus lisible, on utilise maintenant vraiment les dimensions (L,M,T - longueur, masse, temps, et on se rappelle [N] = [L][M][T^{-2}])



On requiert l'homogénéité de l'équation, donc on se retrouve avec



Donc, on voit que


Et donc si tu augmentes le masse d'un facteur 207, le rayon diminue d'un facteur 207.


Remarque : on aurait pu ne pas contracter . On aurait eu alors un dimension en plus, le Coulomb, et une inconnue en plus (la puissance de e dans l'analyse dimensionnelle). On aurait eu alors 4 équations à 4 inconnues.

[Skullkid]

Salut, je ne sais pas quelle solution "quantique" ton prof a proposé mais la solution de Mathusalem est pour moi la plus élégante possible, puisque la plus "physique" (ne jamais faire de calculs avant d'en connaître le résultat).

Enfin vu la tête de la solution, je pense que ça doit pas être trop dur à comprendre finalement. Cela s'inspire de la méca classique céleste, non ?

Si tu utilises un modèle purement classique, tu pourras trouver une relation entre l'énergie de l'atome et son rayon, ou entre la vitesse du muon, sa masse et le rayon de l'atome, mais tu ne pourras pas aller plus loin, puisqu'on ne te donne ni l'énergie fondamentale de l'hydrogène muonique, ni la vitesse du muon. Il te faut un modèle quantique qui va faire naturellement apparaître des quantifications. Même si les équations vont avoir à peu près la même tête que celles de la mécanique céleste classique, la différence est tout de même fondamentale !

[globule rouge]

Merci pour vos messages Math et Skullkid

Alors j'ai la flemme de taper en Latex (je suis pas sur l'ordi ^^) mais je vais tout de même essayer de vous expliquer.

La correction de mon prof tient en une ligne de calculs qu'il a ponctué de quelques explications dont je n'ai plus grand souvenir puisque je n'arrivais pas à comprendre grand' chose sur le moment ^^

Alors nous considérons tout d'abord la relation suivante mv²/r=ke²/r² d'après la méca classique, en mettant de côté l'aspect probabiliste de la position de l'électron.
Or L= OM ;)(mv ) d'où L= =mrv (je ne me souviens plus de l'explication mais cela avait un rapport avec la seconde loi de Kepler qui concerne l'aire décrite par la particule le long de son orbite)
et v= /mr et par suite m ²/m²r³=ke²/r²

Enfin r= ²/mke²


Voilà, cela rejoint le résultat de ton explication, Mathusalem, que je vais essayer de relire attentivement

Je m'y pencherai ce soir sur l'ordi pour plus de confort.

Merci encore à vous !

[Skullkid]

Dans l'explication de ton prof, la quantification apparaît quand il dit que L = ;). Tu peux prouver classiquement que L est constant (c'est la loi des aires) mais il te faut un soupçon de quantique pour savoir que le L de l'état fondamental de l'hydrogène muonique est égal au L de l'état fondamental de l'hydrogène standard, c'est-à-dire ;). Cela dit c'est une belle solution aussi.

[globule rouge]

Ok, reprenons depuis le début du message de Mathusalem (dont je trouve la solution particulièrement élégante, c'est vrai, car il utilise exclusivement de l'analyse dimensionnelle) :)

Qu'appelles-tu E ? Est-ce le champ électrique créé par le proton ? Et le petit omega désigne-t-il la vitesse angulaire de l'électron ?

[Skullkid]

En fait le but de ces formules est de faire des liens entre les dimensions des différentes grandeurs qui interviennent dans le problème. E = ;);) est la formule donnant l'énergie d'un photon de pulsation ;). Elle n'a donc rien à voir en soi avec le problème traité, elle sert juste à dire que ;) c'est une énergie fois un temps (ou une action, si on veut être pédant).

[globule rouge]

D'accord, je vais essayer de me documenter !

Sinon, le h barré est-il une énergie se propageant le long d'un cercle ?

[Mathusalem]

D'accord, je vais essayer de me documenter !

Sinon, le h barré est-il une énergie se propageant le long d'un cercle ?

le h barré (ache barre), c'est une constante. C'est enfait la 'constante quantique' (de Planck). C'est pas évident à expliquer sans avoir fait de la quantique, mais dès que tu considères un système quantique (c'est-à-dire suffisament petit..) t'as tout le temps un hbar qui sort.
Par exemple, un oscillateur harmonique de pulsation ne peut pas avoir n'importe quelle énergie.
Dans un oscillateur classique, pour une constante de raideur fixe, t'as une pulsation fixe . Il peut prendre n'importe quelle énergie suivant l'élongation maximale qu'on lui donne

L'oscillateur quantique, c'est pas tout à fait ça.
La plus petite énergie qu'il peut avoir est . L'énergie immédiatement plus grande qu'il peut avoir c'est . Enfait, les niveaux d'énergie sont .
Donc tu vois que l'énergie est 'quantifiée'. Elle est discrète, et ne peut varier que par 'quants' de . Entre un niveau d'énergie et un autre, tu ajoutes-soustraits une quantité fixe, . Et cette quantité dépend de .

Donc tu le retrouves un peu partout. Une particule possédant une certaine énergie E, aura une pulsation selon

Pour l'analyse dimensionnelle, tout ce que tu dis c'est : j'ai un problème quantique, donc y aura du dedans. Quelle est la dimension de ? Je connais une loi qui me permet de conclure que c'est une Energie fois un temps (ou une action, si effectivement on tient à être pédant).