Aide pour les primitives

par **quaresma** » 27 Avr 2006, 12:25

bonjour,
j'ai bcp de mal a comprendre comment faire pour trouver la primitive d'une fonction.
pour les fonctions de bases genre f(x) = x, c'est simple, ca fait F(x) = x²/2.

Mais lorsque c'est des equations du style de l'image ci-dessous c'est plus dur. Pouvez-vous m'aider a comprendre?

merci beaucoup pour votre aide

par **fonfon** » 27 Avr 2006, 12:35

Salut , on a f(x)=6x(3x²1)² on remarque que c'est de la forme u'(x)*u(x)²

donc
Idée: f=u^n*u' alors F=(u^(n+1))/(n+1)

on pose u(x)=3x²+1 donc u'(x)=6x donc f(x)=u'(x)*u(x)^n
donc une primitive sera
F(x)=(u(x)^(n+1))/(n+1)+k avec k:cste
F(x)=((3x²+1)^3)/3+k avec k:cste

A+

par **Fabrej2001** » 27 Avr 2006, 14:52

Alors par exemple pour le a), on sait que c'est la dérivée d'une fonction, donc on peut écrire :
(6x+3)/(x²+x+2)²=(u'v-uv')/v²
On peut facilement déduire v=x²+x+2
donc
f(x)=(u'(x²+x+2)-u(2x+1))/(x²+x+2)²
On peut observer que si u=-3, alors :
u'v-uv'=0(x²+x+2)-(-3(2x+1))=6x+3
On peut donc en déduire :
F(x)=-3/(x²+x+2)
En bidouillant un peu, parfois on trouve la solution facilement. Bonne chance pour la suite !!!

par **zell** » 27 Avr 2006, 14:58

je pense pareille ke toi fabredg et est ce ke tu pourai maider pour le mienSVp

par **Fabrej2001** » 27 Avr 2006, 15:04

Excuse moi, mais je ne comprends pas ta demande !!! Tu veux que je t'aide à faire les autres ???

par **fonfon** » 27 Avr 2006, 17:39

Re, je vois que tu as changé ton texte donc je t'en refait une

pour m)

on remarque que f(x) est de la forme

donc une primitive sera de la forme

donc on pose

donc

alors on a :

où k:cste
donc

où k:cste

A+

par **allomomo** » 27 Avr 2006, 18:11

Salut,

n -

o -

par **fonfon** » 27 Avr 2006, 18:14

Re, j'en refait 2) et les autres c'est du même style que toutes celles qui t'ont été données

b)

on remarque que f est de la forme

à une constante près donc une primitive est de la forme

avec k:cste

on pose

donc

d'où

avec k:cste

j)

c'est de la forme

à une constante près donc une primitive est

avec k:cste

bon pour les autres tu peux te debrouiller

A+

par **quaresma** » 27 Avr 2006, 22:41

merci a tous pour vos exemples.
Ce que je ne comprend pas, c'est d'où vous sortez les formules du genre:

-u'(x)*u²(x) ; u'(x)*u(x)^n ..........

moi je ne les ai nulle part ds mon cours :mur:

par **nyafai** » 27 Avr 2006, 23:18

bonjour,
je pense que ce qui est important à comprendre, c'est qu'il n'y a pas de méthode systématique pour trouver la primitive d'une fonction. ce n'est pas du tout comme calculer la dérivée d'une fonction! D'ailleurs il existe de nombreuses fonctions dont tu ne peux pas calculer la primitive (par exemple sinx/x tu peux chercher longtemps). En fait en général, on essaie de se ramener à des calculs de primitives simples comme dans les exemples qui t'ont été donnés.

Pour ce qui est de : -u'(x)*u²(x) ;u'(x)*u(x)^n , en fait c'est tout simplement le tableau des dérivées classiques lues à l'envers :
(-u^3)'=-u'(x)*u²(x) donc une primitive de -u'(x)*u²(x) est -u^3
(u^(n+1)/(n+1))'=u'(x)*u(x)^n ( celle la tu la retrouveras vraiment souvent et je te conseille d'apprendre ca par coeur)
bonne continuation

par **mln** » 27 Avr 2006, 23:29

Ca vient du fait que :
Soient f et u, 2 fonctions dérivables et composables
alors :
(f(u))' (x)= u'(x)f'(u(x))

Tu essaie donc d'identifier f et u dans ton intégral
par exemple, pour :

ici

,

on reconnait

ici

Donc

J'espère que ca pourra t'aider a comprendre comment on calcule ces primitives
Bon courage

par **quaresma** » 28 Avr 2006, 17:47

Fabrej2001 a écrit:Alors par exemple pour le a), on sait que c'est la dérivée d'une fonction, donc on peut écrire :
(6x+3)/(x²+x+2)²=(u'v-uv')/v²
On peut facilement déduire v=x²+x+2
donc
f(x)=(u'(x²+x+2)-u(2x+1))/(x²+x+2)²
On peut observer que si u=-3, alors :
u'v-uv'=0(x²+x+2)-(-3(2x+1))=6x+3
On peut donc en déduire :
F(x)=-3/(x²+x+2)
En bidouillant un peu, parfois on trouve la solution facilement. Bonne chance pour la suite !!!

ah tiens MIRACLE pour celle-ci j'ai compris merci bcp !

par **quaresma** » 04 Mai 2006, 20:30

pensez-vous que mes primmitives st bonne lol ? :mur:

par **fonfon** » 04 Mai 2006, 20:57

Salut,

Non

pour la 1) je trouve

pour la 2) je trouve

j'ai pas trop le temps d'ecrire comment j'ai fait peut-être que quelqu'un te repondra sinon je te repondrai demain

A+

par **quaresma** » 04 Mai 2006, 20:59

OK j'espere que tu auras le tps, car je lutte bcp qd même pour essayer de comprendre.
Merci pour ta réponse en tout cas :help:

par **fonfon** » 05 Mai 2006, 07:09

Salur

f(x)=(x+1)(x²+2x-1)^4

Idée:

donc

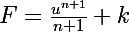
avec k cste

on pose

donc

on obtient donc

donc

avec k:cste

par **fonfon** » 05 Mai 2006, 07:23

RE, j'ai oublié la 2eme c'est du même genre donc

Idée:

donc

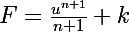
on pose

donc

soit

donc

k:cste

soit

A+

par **quaresma** » 05 Mai 2006, 15:34

fonfon a écrit:Salur

f(x)=(x+1)(x²+2x-1)^4

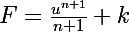
Idée: donc avec k cste

on pose donc

donc

on obtient donc
donc
avec k:cste

salut,
pourquoi ne garde t'on pas 2x+2 dans ce cas ->

ici

où est passé le 2(x+1) ? je ne comprend pas.

et à la fin pourquoi le (x²+2x-1) n'est pas à la puissance 5 ?

Je sais, c'est bcp de questions, mais je ne comprend pas... :marteau:

par **quaresma** » 06 Mai 2006, 23:17

up :help:

par **quaresma** » 28 Mai 2006, 18:51

pouvez-vous me dire si ce que j'ai trouvé est juste :

f) (3/2)/(2x+5)² + C
g) (racine de x) + 4x + C
h) -(x/x²)cos(x²-4) + C
i) 4/2 racinede(x-5) + C

merci encore :briques:

Aide pour les primitives

aide pour les primitives

Qui est en ligne