Très Belle arithmétique

[laya]

Un exercice maintenant connu et reconnu, il n'est pas rare d'avoir des exos de la même veine aux OIM .
Soient a et b deux entiers naturels.
Montrer que si est un entier alors c'est un carré parfait.

Complément : l'une des solutions proposées est basée sur la descente infinie. Si inconnue, Google devrait faire l'affaire. Il faut vraiment connaître cette technique.

[Zweig]

En effet, archi connue (enfin, dans le monde des OIM)

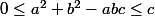
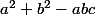
Complément 2 (généralisation) : Si , et sont des naturels non nuls tels que , alors est un carré parfait.

La première peut se résoudre par récurrence aussi : http://www.maths-forum.com/a-b-ab-1-n-94054.php

[laya]

En effet, archi connue (enfin, dans le monde des OIM)

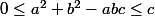
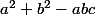
Complément 2 (généralisation) : Si , et sont des naturels non nuls tels que , alors est un carré parfait.

La première peut se résoudre par récurrence aussi : http://www.maths-forum.com/a-b-ab-1-n-94054.php

Ayye, j'aurais dû faire une recherche dans le forum avant d'ouvrir cette discussion. Tant pis.
Je propose que les intéressés se focalisent plutôt sur la généralisation que tu as proposée.

[benekire2]

Salut ,

J'en avais carrément chié "à l'époque" : http://www.maths-forum.com/arithmetique-relativement-simple-93504.php , c'est justement à cette periode (un peu plus d'un an) où j'ai commencé les maths :ptdr: