Histoire de droites..

[Maxxie]

Bonjour,

Je suis en MPSI à Lyon, et avec pas mal de difficultés.. Je but toujours sur des choses qui devraient être "triviales" en prepa. :hein:
En fait, mon exercice concerne la géométrie plane.

Voilà :

Dans (O,i,j), on considère A(a;0), B(0;b) et M(u;v).

1.Expliciter les équations cartésiennes ou polaires, selon la commodité, des droites en questions.
2.Donner l'équation sous forme de polynôme vérifiée par u et v lorsque (OM) est bissectrice de (AM) et (BM).
3....

Pour la première question, j'ai :

(MA) : vu + (a-u)v - av = 0
(MB) : (u-b)u -uv + bu = 0
(AB) : r = OH/cos(OM;OH) avec H projeté orthogonal de O sur (AB)

Pour la 2eme question, j'ai commencé par chercher quelque chose en disant que (OM) bissectrice de (AM) et (BM) ssi d(OM;AM)=d(OM;BM)
Mais ça n'entraine rien d'intéressant.

Ensuite j'ai essayé d'utiliser H pour me ramener à des triangles rectangles.. Rien de concluant.
Avez-vous une autre idée svp ?

Merci de vos futures réponses (et pour votre indulgence.. C'est mon premier message).

PS : Question à part.. Mon professeur m'a dit qu'il estimait bon que je passe en moyenne 1h30 par exercice.. 2h pour deux questions, ce n'est pas inquiétant ?

[Pythales]

Les équations de tes droites ne contiennent ni x ni y !
Le coefficient directeur de AM vaut , celui de BM vaut
Ecris les équations de droites dont tu connais le CD et passant par un point donné.
L'équation de AB est facile.
Si est l'angle de OM avec Ox, 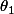celui de AM et 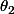celui de BM, écris que et utilise la trigo.

[Maxxie]

On a M(u,v) et non pas M(x,y) qui varie.. Je pensais qu'on devait écrire l'équation sous la forme : au+bv+c=0 (a et b n'ont rien avoir avec l'énoncé pour cette équation).

Sinon.. J'ai rien compris à ce message.. Dsl.. =S

C'est quoi l'histoire des coef directeurs ? Dans le cours, je me souviens seulement avoir vu qu'une équation cartésienne d'une droite était ax+by+c=0..

Merci d'avoir répondu si vite :)

[Pythales]

Si on écrit l'équation de la droite y=mx+p, m est le coefficient directeur.
Curieux de ne pas connaître ça en MPSI. Peut-être l'appelles-tu comme anciennement : la pente.

[Maxxie]

En gros, je me compliquais la vie avec mes équations ax+by+c...

Ce qui est bizarre, c'est qu'on a jamais fait d'exercice avec les coef directeurs en classe. C'est la seule méthode ?

En ce qui concerne mon équation polaire, pourquoi est-elle fausse ?

[Pythales]

Tu dois exprimer r en fonction de , a et b
Mais c'est plus simple en cartésiennes

[Maxxie]

C'est juste que j'ai besoin des coordonnées polaires de (AB) pour la suite en fait..

Je suis quand même sceptique pour (MA) et (MB).. Le professeur va évidemment voir que la solution ne vient pas de moi, même si je crois avoir compris la démarche..

[benekire2]

Pour la question 2:

Qu'est-ce qu'une médiatrice ? ... C'est la droite telle que si tu prend un point dessus ils sont a la même distance des deux droites que tu bissecte. Résultat : Formule donnant la distance a une droite ... .

[Maxxie]

Pourquoi la médiatrice..? (Excusez-moi, je suis vraiment perdu..)

[Pythales]

Pour MA et MB, tu peux dire que leur équation est de la dorme px+qy+1=0 et tu calcules p et q en exprimant qu'elles passent, l'une par A et M, l'autre par B et M.

[Maxxie]

C'est juste que j'ai besoin des coordonnées polaires de (AB) pour la suite en fait..

Je suis quand même sceptique pour (MA) et (MB).. Le professeur va évidemment voir que la solution ne vient pas de moi, même si je crois avoir compris la démarche..

Ok. Pour le coup, je me fais honte à moi-même.. La réponse était évidente, même sans les coef directeurs.. Est-ce que (MA) : vx+(a-u)y=av ?
Merci de cette patience !

[benekire2]

Oups, je parlais de bissectrice bien entendu .. désolé :happy2:

Et voilà je peu plus éditer, mon erreur sera gravé a jamais ..

[Maxxie]

D'accord.. Mais je n'étais arrivé à rien en utilisant la définition..

Et sinon.. Est-ce que, pour la question 2, il est envisageable de faire intervenir un cercle ?

[benekire2]

Je ne vois pas pourquoi tu en aurait (réellement) besoin ?

[Maxxie]

Parce que je n'arrive pas à me servir de la définition de la bissectrice..

Ne me frappes pas... :marteau:

Au fait..

Est-ce que (MA) : vx+(a-u)y=av ?

[benekire2]

Pourquoi je te frapperais ? :ptdr:

Bon, si tu lis mon message instructif précédent de 18h36 je donne une caractérisation des bissectrices par la distance d'un point a une droite,

normalement tu connais cette formule.

[Maxxie]

d(M, (D) ) : |ax + by + c|/(racine(a² + b²)) avec M(x;y)

D'accord.

Tu veux dire qu'il faut résoudre :
d(M;(AM))=d(M;(BM)) ?

Si c'est ce que tu me conseilles de faire, je suis content parce que j'ai eu cette idée.. Moins content parce que je ne suis aboutit à pas grand chose.. :/

Je radote mais j'ai bien : (MA) : vx+(a-u)y=av ?

Encore merci de cette aide !

[Pythales]

C'est bon mour (MA).
L'avantage du coef directeur, c'est que ça représente la tangente de l'angle de la droite avec Ox.
Pour la bissectrice, il faut partir de puis, comme je l'ai indiqué, passer aux tangentes

[Pythales]

Avec cette méthode, tu devrais trouver
avec

[benekire2]

d(M, (D) ) : |ax + by + c|/(racine(a² + b²)) avec M(x;y)

D'accord.

Tu veux dire qu'il faut résoudre :
d(M;(AM))=d(M;(BM)) ?

Si c'est ce que tu me conseilles de faire, je suis content parce que j'ai eu cette idée.. Moins content parce que je ne suis aboutit à pas grand chose.. :/

Je radote mais j'ai bien : (MA) : vx+(a-u)y=av ?

Encore merci de cette aide !

Oui c'est ça ..