Suite croissante
26 messages
- Page 2 sur 2 - 1, 2
OK je me disais aussi !
Tu sais que U(n+1)-Un = 4*(5/12)^n
Tu écris cette égalité pour tous les n en partant de 0
^{0})
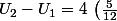^{1})
etc ...
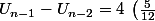^{n-2})
^{n-1})
Ensuite tu fais la somme de toutes ces égalités
A gauche presque tous les termes s'en vont, il reste juste le 1er et le dernier
A droite tu factorises par 4
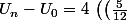^{0} + \left(\frac{5}{12}\right)^{1} + \cdots + \left(\frac{5}{12}\right)^{n-2} + \left(\frac{5}{12}\right)^{n-1}\right))
Tu as peut-être vu la formule pour calculer la somme des termes d'une suite géométrique
^{n}}{1- \left(\frac{5}{12}\right))
Et au final
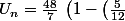^{n}\right))
Du coup la suite converge vers 48/7
Tu sais que U(n+1)-Un = 4*(5/12)^n
Tu écris cette égalité pour tous les n en partant de 0
etc ...
Ensuite tu fais la somme de toutes ces égalités
A gauche presque tous les termes s'en vont, il reste juste le 1er et le dernier
A droite tu factorises par 4
Tu as peut-être vu la formule pour calculer la somme des termes d'une suite géométrique
Et au final
Du coup la suite converge vers 48/7
26 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
